問題PDF
(1) 正解率;75.9%
Aさんは2400円、Bさんは3900円持っています。
同じ値段のケーキをAさんは3個、Bさんは5個買ったところ、
AさんとBさんの所持金の比が5:7になりました。
ケーキ1個あたりの値段は何円ですか。
(2) 正解率;20.3%
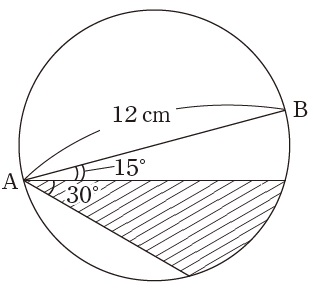
図のようなABを直径とする円があります。
斜線部分の面積は何cm2ですか。
(3) 正解率;76.3%
20cmの紙テープが何枚かあり、図のようにのりしろの部分を2cmとして貼り合わせました。
貼り合わせて1枚につながった紙テープを、2cmをのりしろとして輪を作り、
この輪を上から見ると円になりました。この円の面積を7850cm2以上にするには、
20cmの紙テープを少なくとも何枚必要ですか。
なお、この問題は解答までの考え方を表す式や文章・図など書きなさい。

(4) 正解率;52.0%
1個50円のお菓子を買いに行くために、買う予定の個数分のお金をちょうど持っていきました。
しかし、1個55円に値上がりしていたので、予定よりも7個少ない個数しか買えませんでした。
持っていったお金は、何円ですか。
最も少ない場合と最も多い場合を、それぞれ答えなさい。
なお、この問題は解答までの考え方を表す式や文章・図などを書きなさい。
@解説@
(1)
ケーキ1個の値段を①とする。
2400-③:3900-⑤=5:7
内項と外項の積から、
(2400-③)×7=(3900-⑤)×5
④=2700
①=675
675円
(2)
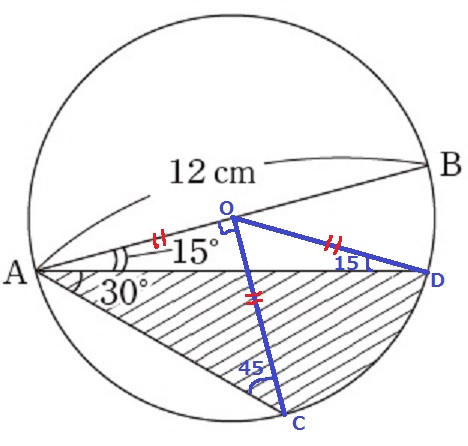
このような補助線をひく。
半径から、△OACの内角は45°-45°-90°の直角二等辺。
△OADは底角が15°の二等辺。

△OADの外角定理から、∠DOE=15+15=30°
∠COD=90-30=60°
【斜線部分=直角三角形OAC+扇形OCD-二等辺OAD】
二等辺OADの高さは、内角が30°-60°-90°の△ODEからDE=3cm
6×6÷2+6×6×3.14×60/360-6×3÷2
=27.84cm2
(3)
円の半径を□とすると、
□×□×3.14≧7850
□×□≧2500
□≧50
□=50cmのとき、円周の長さは、
50×2×3.14=314cm
紙テープを輪っかにすると、のりしろの場所とのりしろのない場所の数は同じ。
紙テープの長さを20-2=18cmと考えて、
314÷18=17.44…
18枚以上の紙をつなげれば条件に適合する。
(4)
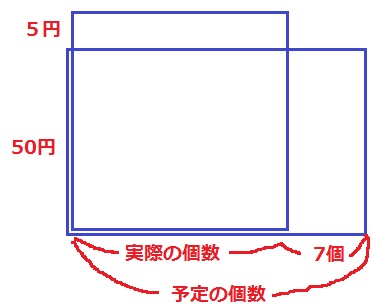
この図をよぎらせる。
ポイントは『7個少ない個数しか買えなかった』。
予定より買えなかった個数分の代金は、
お菓子7個分ちょうどとは限らず、6個分+1円でも7個少ない数になる。
55×6+1=331円
55×7=385円
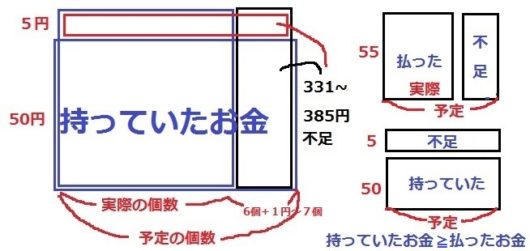
1個50円から55円に値上がりしたことで、331~385円の不足分が発生した。
5円の値上がりから予定の個数の範囲を確定する。
(*持っていたお金≧払ったお金なので、赤枠の面積≧黒枠の面積)
331÷5=66.2個
→331円は不足を最も少なく見積もったケース。個数は整数なので切り上げて67個。
385÷5=77個
予定の個数は、67個~77個の範囲。
持っていったお金は、
最も少ない場合…67×50=3350円
最も多い場合…77×50=3850円
難関中(算数科)解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д`)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい!
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ!
勉強方法の紹介…いろいろ雑記φ(・・。)
QUIZ…☆4以上はムズいよ!
noteも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのnote
サボのツイッターはコチラ→



コメント