大問1(小問集合)
(1)
-42+3×(-2)
=-16-6
=-22
(2)
(9x-4y)-3(x-5y)
=9x-4y-3x+15y
=6x+11y
(3)
49x2+28x+4 ←49と4は平方数
=(7x+2)2
(4)
7/√2-√18
=7√2/2-3√2
=√2/2
(5)
(x+1)(x-5)=7
x2-4x-5=7
x2-4x-12
=(x+2)(x-6)=0
x=-2、6
(6)
一次関数;y=ax+b
(x、y)=(4、3),傾きa=-2を代入する。
3=-2×4+b
b=11
y=-2x+11
(7)
y=16/xについて、
x=1のとき、y=16
x=4のとき、y=4
変化の割合=(yの増加量)÷(xの増加量)
=(16-4)/(1-4)
=-4
(8)

yの最小値が負→グラフは上に凸である。
原点Oから最も遠いx=-3のとき、y=-27
y=ax2に代入して、
-27=9a
a=-3
(9)

多角形の外角の和は360°
360-(70+75+54+66)=95°
x=180-95=85°
(10)

平行線と線分の比。
AE:EB=DF:FC
DF=4×4/6=8/3cm
(11)
半径3cmの円の面積は9πcm2
扇形は円の一部→割合は9πのうち6π、6π÷9π=2/3
弧の長さは、3×2×π×2/3=4πcm
@余談@
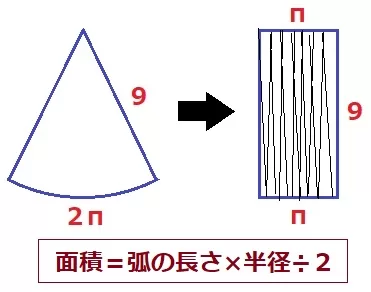
扇形の面積は、弧の長さ×半径÷2で求めることができる。
たとえば、弧の長さ2π、半径9であれば、2π×9÷2=9π
弧の長さを底辺、半径を高さと見立てた三角形に置き換えることができる。
中学受験の世界ではスーパー三角形というそうな( ´д)ヒソ(´д`)ヒソ(д` )
理屈は円の面積の公式と同じで、扇形を細かくスライスして互い違いに並べると、
縦が半径、横が弧の半分の長さである長方形になるから。
本問で適用すると、6π×2÷3=4πcm
(12)

①OXとOYから距離が等しい点の集合→∠YOXの二等分線
②OP=AP→PはOとAから等距離にある→OAの垂直二等分線
交点がP
大問2(数量変化)
(1)
重複部分は等辺6cmの直角二等辺。
y=6×6÷2=18
(2)
0≦x≦8は、等辺xcmの直角二等辺。
y=1/2x2
(3)

直角二等辺はFがBに着くまで移動する。
全部が中に入ってしまうと、y=8×8÷2=32で変わらない。
y=10のタイミングは0≦x≦8しかない→前問利用
1/2x2=10
x2=20
x>0より、x=2√5
(4)
0≦x≦8…y=1/2x2より放物線
(底辺と高さがともに伸びるから)
8≦x≦16…y=32で一定。
ウ
大問3(データの活用)
(1)①

A13人の中央値は(13+1)÷2=7番目→25~30の階級
B15人の中央値は(15+1)÷2=8番目→30~35の階級
Bの方が大きい。×
イ
②
35分未満の相対度数は、A9/13、B9/15
分子共通→分母が大きいBの方が小さい。〇
ア
(2)①

範囲=最大値-最小値
45-25=20分
範囲が+1なので、24か46が追加される。
ここで、先ほどの度数分布表を用いる。
20~25未満の階級は0人だから、46が追加される。
最大値は46分
②

15人の第3四分位数(Q3)は上位7人の真ん中→上から4番目
度数分布表と照らし合わせて、足りないデータの場所を調べると、
35以上はすべてのデータがそろっている。Q3は42分
③

四分位範囲=Q3-Q1
下から4番目である第1四分位数(Q1)=42-14=28
平均34からの差をとる。
+46-44=+2
-2をつくって+2と相殺すれば平均34になる。
34-2=32
不明なデータは28・32・46の3つだから、2番目は32分
大問4(確率)
(1)

PA=PB→PはAとBから等距離にある→ABの垂直二等分線上にPがある。
三角形ができるのは上図の5点
全体は6×6=36通り
確率は5/36
(2)

ABを対称の軸として、△OABを対称移動した三角形が該当する。

これと面積が同じ三角形は他にないか?→等積変形
ABに平行な線を引くと、もう2点ある。
確率は3/36=1/12
大問5(平面図形)
(1)
△ADE≡△HCBの証明。

仮定より、AD=HC
平行四辺形の対辺は等しいから、DE=CB
ED//CBの同位角と二等辺ABCの底角より、∠ADE=∠HCB
2辺とあいだの角が等しいから合同。
(2)

合同の対応する辺で、HC=3cm
AH=10-3=7cm
AB//GCより、対頂角と錯角の2角相等で△CGH∽△ABH
相似比はCH:AH=3:7

方針【△ABC→△HBC→△CGH】
△CGHの面積は、25×3/10×③/⑦=45/14cm2
大問6(数量変化2)
(1)

B・Cをグラフに書き込む。
Aの変化量は(-6)から(-2)に切り変わる。
このタイミングでB(+4)と交わる。
そこから10分後にA(-2)とC(+2)が交わる。
この10分がポイントになる。

●から10分前のbまでさかのぼる。
変化量はA(-2)、C(+2)だから、逆再生すると1分あたり4cmの差が生まれる。
bでは、4×10分=40cm差

●からbまで、BとCは40cm差が生まれる。
1分あたり4-2=2cm差だから、b=40÷2=20分

●から0分までさかのぼる。
A(-6)とB(+4)は逆再生1分で10cm差だから、a=10×20分=200cm
a=200、b=20
(2)

↑ここを見る。
同じ高さまで、B(+4)は20分かかった。
A(-2)は変化量が半分だから、時間は2倍の40分かかる。
Aの水がなくなるのは、20+40=60分後
講評は後日。


コメント