平均52.44点（前年比＋3.11点）
問題はコチラ→ＰＤＦファイル
大問１（小問集合）
しょっぱなから面食らった人は少なくないはず。
（１）
〔前日の最低気温〕＋２℃＝－３℃
前日の最低気温＝－３－２＝－５℃
（２）
□×□＝50ｃｍ2
□＝√50＝５√２ｃｍ
（３）
封筒…ａｇ
５枚の便箋…５ｂｇ
これらが60ｇより重かったので、ａ＋５ｂ＞60
ア
（４）
『ＢがＣと重なる』
→折り目を対称の軸とすると、ＢとＣは対応する点。
すなわち、折り目はＢとＣの垂直二等分線。
折り目となる『線分』なので、△ＡＢＣ内部だけの線がベターかも。
大問２（小問集合２）
（１）
整数の証明。
３桁の自然数で百の位がａ、十の位がｂ、一の位が５
→100ａ＋10ｂ＋５ …ア
５の倍数であることを証明したいので、５×（ イ ）の形に変形する。
100ａ＋10ｂ＋５＝（20ａ＋２ｂ＋１）
イ…20ａ＋２ｂ＋１
（２）
１文目から、ｘ＋ｙ＝6300
ア…ｘ＋ｙ
２文目から、ポロシャツが２割引き→ｘ×0.8円
トレーナーは800円安く買った→ｙ－800円
0.8ｘ＋ｙ－800＝5000
イ…0.8ｘ＋ｙ－800
*計算式のみでＯＫ。
答えを求めると、ｘ＝2500、ｙ＝3800
（３）
ｙ＝ｘ2より各々の座標を算出。
Ａ（－３、９）→Ｂ（２、４）
右に５、下に５だから傾きは－５/５＝－１
Ａから右に３、下に３で、切片は９－３＝６
ＡＢ；ｙ＝－ｘ＋６
ｙ＝０を代入。
０＝－ｘ＋６
ｘ＝６
Ｃ（６、０）
＠別解＠
①傾きが－１なので赤い三角形は直角二等辺三角形。
切片６さえわかれば、Ｃ（６、０）と即答できる。
②相似を利用すれば、Ｃのｘ座標は４＋２＝６
（４）
ＡからＥに着くには、出目の合計が４か９。
◆出目の和が４
（１、３）（３、１）（２、２）
◆出目の和が９
（６、３）（３、６）（５、４）（４、５）
以上、７通り。
７/36
大問３（平面図形）
（１）
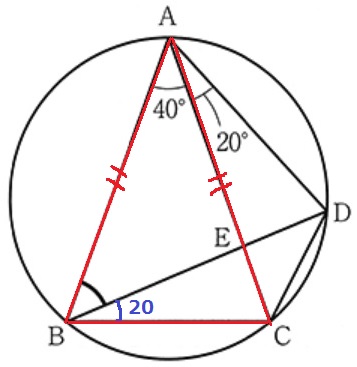
弧ＣＤに対する円周角より、∠ＤＢＣ＝20°
△ＡＢＣは二等辺だから、∠ＡＢＣ＝（180－40）÷２＝70°
∠ＡＢＥ＝70－20＝50°
（２）①
△ＡＢＥ≡△ＡＣＤの証明。
基本の証明問題なのでとりたい。
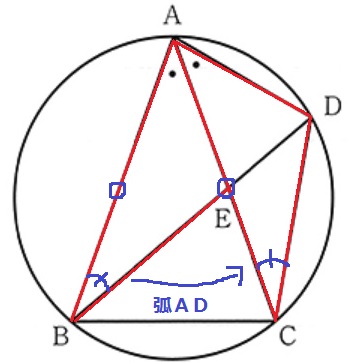
問題文から１辺と１つの角が等しいとわかっているので、
弧ＡＤに対する円周角からもう１つの等角を指摘する。
１辺と両端角より合同。
②
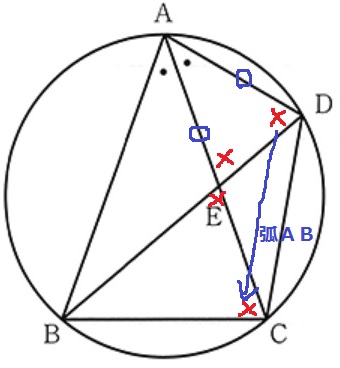
前問の合同より、ＡＤ＝ＡＥ
△ＡＤＥは二等辺となり、底角が等しい。
各々の底角を、対頂角と弧ＡＢに対する円周角で移動させると、
△ＢＣＥの底角も×で等しくなり、二等辺基本の。
△ＡＢＣも二等辺で、底角が×で等しい。
つまり、３つの二等辺三角形はすべて相似で、辺の比は３：３：２である。
△ＡＢＣ∽△ＢＥＣより、ＣＥ＝２×２/３＝４/３ｃｍ
ＡＥ＝３－４/３＝５/３ｃｍ
ＡＤ＝ＡＥ＝５/３ｃｍ
大問４（数量変化）
（１）
タオル１枚につき100円かかるので、傾きは100。
初期費用3000円から、ｙ＝100ｘをｙ軸に対して＋3000平行移動する。
ｙ＝100ｘ＋3000
（２）
Ａ店…図より、6500円
Ｂ店…前問の式にｘ＝30を代入。 100×30＋3000＝6000円
したがって、Ｂ店が500円安い。
（３）
Ｂ店をグラフに乗せる。
目盛りの幅に注意！横軸は10、縦軸は500ずつ。
前問でｘ＝30のときｙ＝6000だったので、
（０、3000）から（30、6000）を通る直線をひく。
40≦ｘ≦80の範囲でＢがＡを下回る範囲を探す。
留意点は、50と60は含まない！
50枚のとき、Ａ店は6500円、Ｂ店は8000円。
60枚のとき、Ａ店は9000円、Ｂ店は9000円と値段が等しいので、
『Ｂ店の方がＡ店よりも安い』にはならない。
51枚以上59枚以下
大問５（データの活用）
（１）
最頻値（モード）は最もあらわれている度数。
階級値で答えること。
すなわち、20と22の平均である21ｍ。
（２）
20ｍ未満の度数は３＋２＋２＝７
７÷50＝７/50＝14/100＝0.14
相対度数であれば0.14だが、百分率なので14％
（３）
中央値と平均値の違い。
標本調査ではよくある記述問題なので、ここも取りたい。
50人の中央値（メジアン）は、25番目と26番目の平均値。
図から頑張って調べると、25番目と26番目も24以上26未満の階級にある。
つまり、中央値は24以上26未満に含まれ、太郎の記録は中央値より小さくなるから、
25番目以内には入らないことになる。
大問６（空間図形）
（１）
立面図…正面からみた図。平面図…上からみた図。
解答では２つ選択する。
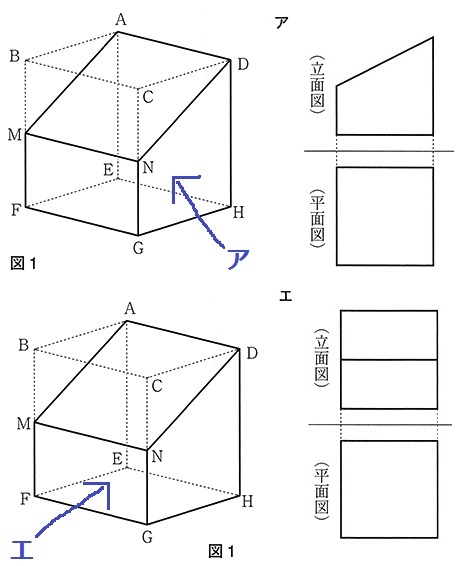
眺める方向だけを変えるので、立体Ｐを傾けたり裏返すのはＮＧ。
平面図は四角形ＡＭＮＤしか見れないので、正方形しかない。
これだけでア・エとしぼれる。
（２）
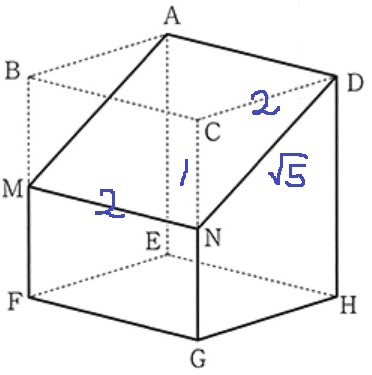
△ＣＤＮで三平方→ＤＮ＝√５ｃｍ
四角形ＡＭＮＤの面積は、２×√５＝２√５ｃｍ2
（３）
ありがたいことにアングルを変えた図が用意されている。
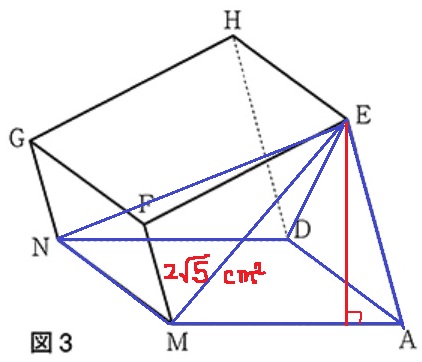
先ほど、四角形ＡＭＮＤの面積を求めたので、
この高さがわかれば四角錘Ｅ－ＡＭＮＤの体積がわかる。
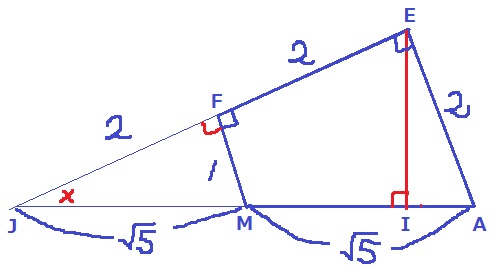
Ｅから垂線をおろし、交点をＩとする。
ＥＦとＡＭの交点をＪとする。
△ＪＦＭ∽△ＪＥＡより、ＦＭ：ＥＡ＝１：２から、
ＪＭ＝√５、ＪＦ＝２
△ＪＦＭ∽△ＪＩＥより、ＪＭ：ＪＥ＝√５：４から、
ＥＩ＝１×４/√５＝４√５/５ｃｍ
したがって、２√５×４√５/５÷３＝８/３ｃｍ3
＠別解＠
高さＥＩについてです。
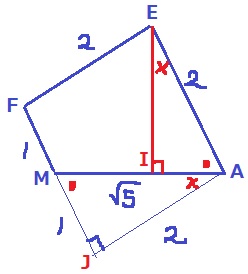
切断された部分を復元すると、△ＭＡＪの辺の比は１：２：√５
△ＭＡＪ∽△ＡＥＩより、ＥＩ＝２×２/√５＝４√５/５ｃｍ
＠別解２＠
前問の答えを無視してもできる。
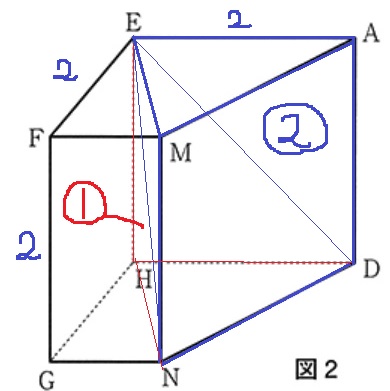
図２を使います。
ＥＭとＨＮは平行。
三角柱ＥＡＭ－ＨＤＮから後ろの三角錐Ｅ－ＨＤＮを引けば四角錘Ｅ－ＡＭＮＤになる。
三角錐は三角柱の３分の１。
三角柱ＥＡＭ－ＨＤＮの体積を③とすると、三角錐Ｅ－ＨＤＮは①、四角錘Ｅ－ＡＭＮＤは②となる。
２×２÷２×２×２/３＝８/３ｃｍ3
形式の変更があるものの、平均点は少しあがった。
大問１
ここで動揺した人は負ける。
大問２
手堅く死守したい。
大問３
（２）②二等辺三角形の相似って見つけにくい感じがする。
等角を認定していくこと。
大問４
グラフの活用は茨城では必須！含む・含まないは確実に。
大問５
昨年より解きやすいかな？推論要素が入ると厄介になる。
大問６
（３）高さはどこか？あとは平面勝負。
公立高校入試解説ページに戻る
コメント