問題はコチラ→ＰＤＦファイル
大問１（小問集合）
（１）
４＋６×（－１/２）
＝４－３
＝１
（２）
（５ａ＋ｂ）/３－（８ａ＋ｂ）/９
＝｛３（５ａ＋ｂ）－（８ａ＋ｂ）｝/９
＝（15ａ＋３ｂ－８ａ－ｂ）/９
＝（７ａ＋２ｂ）/９
（３）
√６（４√２＋１） ←√６＝√２×√３
＝（√２×√３）×４√２＋√６ ←√２×√２＝２
＝８√３＋√６
（４）
７ｘ－５＝９ｘ＋３
２ｘ＝－８
ｘ＝－４
（５）
ｙ＝－２ｘ＋１ …①
４ｘ＋ｙ＝７ …②
①を②に代入。
４ｘ＋（－２ｘ＋１）＝７
２ｘ＝６
ｘ＝３
①に代入、ｙ＝－２×３＋１＝－５
ｘ＝３、ｙ＝－５
（６）
ｘ2＋９ｘ＋８
＝（ｘ＋８）（ｘ＋１）＝０
ｘ＝－８、－１
（７）
最頻値（モード）は最もあらわれている値。
16～20分の階級の階級値である18分。
あ…１、い…８
（８）
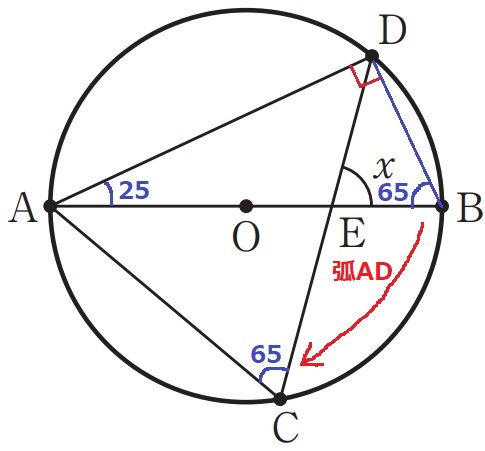
ＤＢに補助線。
直径に対する円周角で、∠ＡＤＢ＝90°
△ＡＢＤの内角から、∠ＡＢＤ＝180－（90＋25）＝65°
弧ＡＤの円周角で、∠ＡＣＤ＝65°
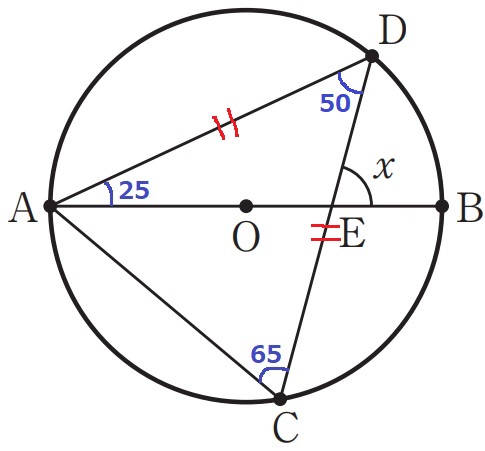
△ＡＣＤは二等辺なので、∠ＡＤＣ＝180－65×２＝50°
△ＡＥＤで外角定理→ｘ＝25＋50＝75°
う…７、え…５
＠別解＠
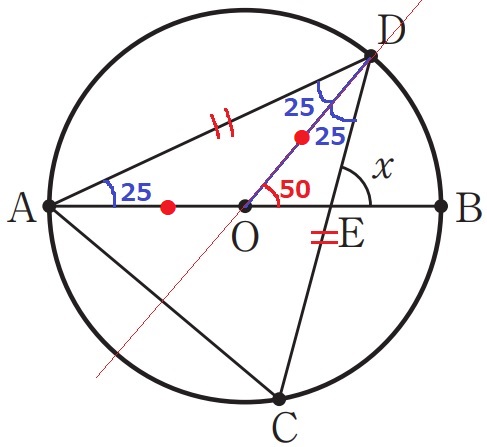
ＤＯに補助線。
半径ＡＯ＝ＤＯから△ＡＯＤは二等辺→∠ＡＤＯ＝25°
△ＡＯＤで外角定理→∠ＤＯＥ＝25＋25＝50°
また、弦ＡＣの垂直二等分線は円の中心Ｏを通る。（ＯはＡとＣから等距離にある）
△ＡＣＤは二等辺だから、ＡＣの垂直二等分線は直線ＤＯである。
ＤＯを対称の軸として、対称性から∠ＡＤＯ＝∠ＣＤＯ＝25°
△ＯＥＤで外角定理→ｘ＝50＋25＝75°
（９）
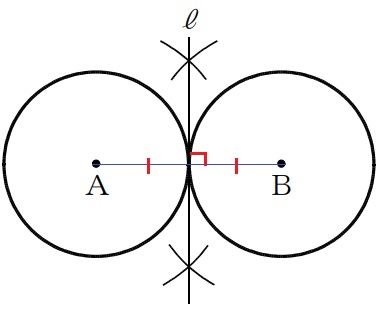
半径と接線は直交する→線分ＡＢ⊥直線ℓ
円Ａと円Ｂは半径が等しい→接点はＡＢの中点
直線ℓはＡＢの垂直二等分線である。
大問２（式の証明）
（１）
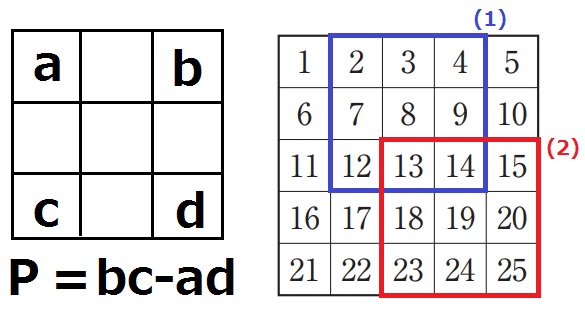
３×３の四隅がａ、ｂ、ｃ、ｄである。
ａ＝２のとき、Ｐ＝４×12－２×14＝20
ａ＝13のとき、Ｐ＝15×23－13×25＝345－325＝20
①…イ、②…ア
＠余談＠
どの９マスでもＰ＝20である。
（２）
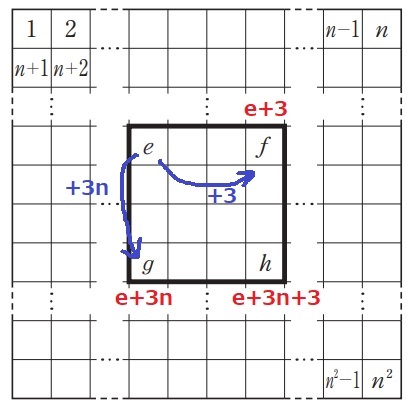
まずはｆ、ｇ、ｈを文字で表す。
ｅの３マス先がｆ。ｆ＝ｅ＋３
（*＋４にしないこと！）
１行はｎマス。左上の１の下がｎ＋１であるように、１つ下の数は＋ｎ。
３行下は＋３ｎだから、ｇ＝ｅ＋３ｎ
ｈ＝ｇ＋３＝ｅ＋３ｎ＋３
これらを式に代入する。
Ｑ＝ｆｇ－ｅｈ
＝（ｅ＋３）（ｅ＋３ｎ）－ｅ（ｅ＋３ｎ＋３）
＝ｅ2＋３ｅｎ＋３ｅ＋９ｎ－ｅ2＋３ｅｎ－３ｅ
＝９ｎ
大問３（関数）
（１）
ｙ＝１/４ｘ2において、
ａ＝０のとき、最小値ｂ＝０
ａ＝－６のとき、最大値ｂ＝９
０≦ｂ≦９
①…エ、②…ク
（２）
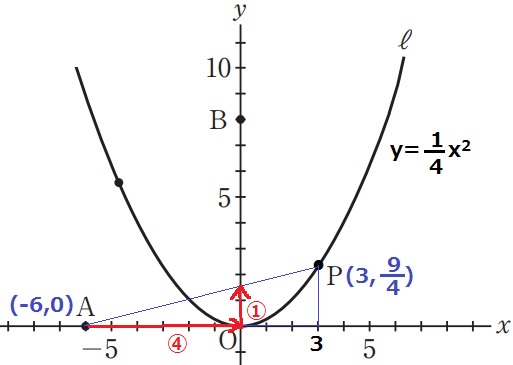
ｙ＝１/４ｘ2にｘ＝３を代入→Ｐのｙ座標は９/４。
Ａ（－６、０）→Ｐ（３、９/４）
右に９、上に９/４なので、傾きは９/４÷９＝１/４
Ａから右に④（＝６）、上に①で切片、６×①/④＝３/２
ｙ＝１/４ｘ＋３/２
③…ウ、④…イ
（３）
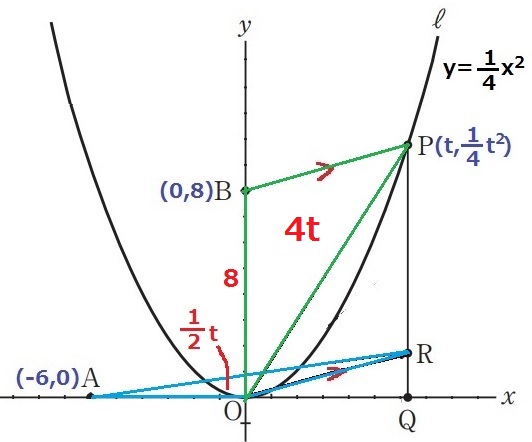
Ｐのｘ座標をｔとする。Ｐ（ｔ、１/４ｔ2）
△ＢＯＰの面積は、８×ｔ÷２＝４ｔ
△ＡＯＲの面積は、４ｔ÷８＝１/２ｔ
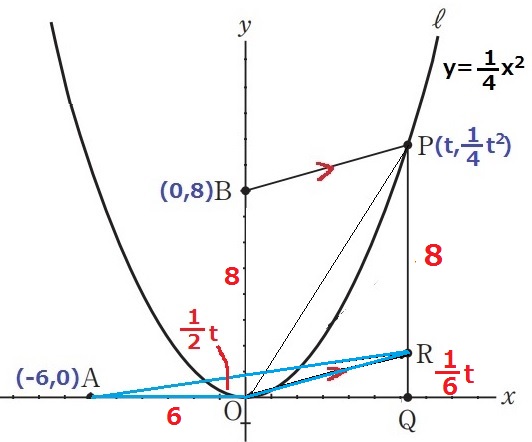
ＲＱは△ＡＯＲの高さなので、ＲＱ＝１/２ｔ×２÷６＝１/６ｔ
四角形ＢＯＲＰは２組の対辺が平行だから平行四辺形。対辺は等しく、ＰＲ＝８
Ｐのｙ座標で等式を立てる。
１/４ｔ2＝１/６ｔ＋８
３ｔ2－２ｔ－96
＝（３ｔ＋16）（ｔ－６）＝０
ｔ＞０だから、ｔ＝６
*最後の因数分解で96の約数がやや多い…。
Ｐのｙ座標はＢより大きいので、１/４ｔ2＞８→ｔ2＞32→ｔ＞５で当たりをつける。
＠別解＠
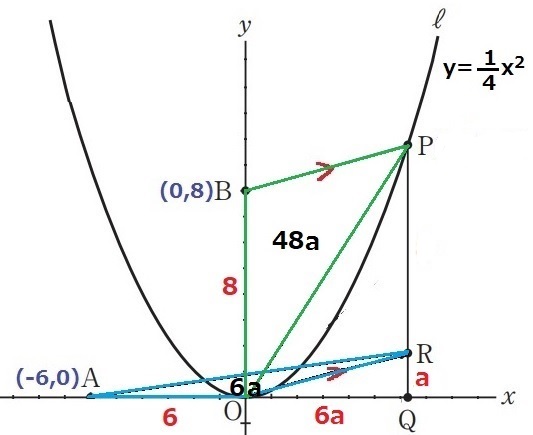
最も短いＲＱの長さをａとする。
△ＡＯＲの面積比は６×ａ＝６ａ
△ＢＯＰの面積比は６ａ×８＝48ａだから、ＯＱ＝48ａ÷８＝６ａ
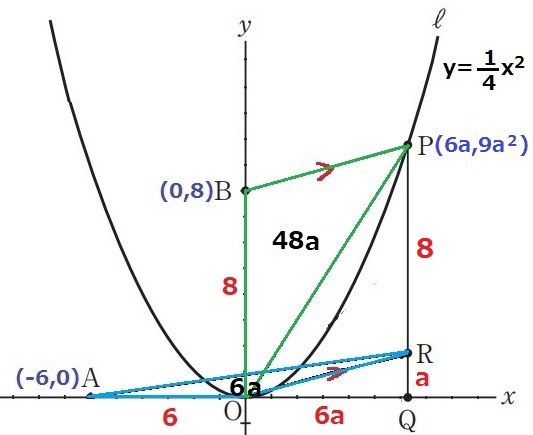
Ｐのｘ座標が６ａなので、これをｙ＝１/４ｘ2に代入するとｙ座標は９ａ2。
Ｐのｙ座標で等式を立てると、９ａ2＝ａ＋８
９ａ2－ａ－８
＝（９ａ＋８）（ａ－１）＝０
ａ＞０なので、ａ＝１
Ｐのｘ座標は、６ａ＝６
＠余談＠
ＯＲは左に６ａ、上にａだから傾きは１/６。
ということは、ＢＰの式はｙ＝１/６ｘ＋８
Ｐはこれとｙ＝１/４ｘ2との交点（ｘ＞０）なので、
１/４ｘ2＝１/６ｘ＋８
３ｘ2－２ｘ－96
＝（３ｘ＋16）（ｘ－６）＝０
…と、先ほどと同じ式がでてくる。
大問４（平面図形）
（１）
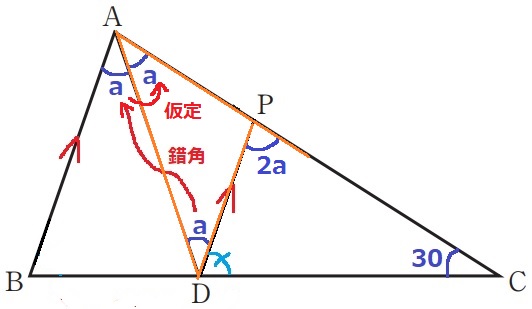
ＡＢ//ＰＤの錯角で、∠ＢＡＤ＝ａ
仮定よりＡＤは∠ＢＡＣの二等分線だから、∠ＤＡＣ＝ａ
△ＡＤＰで外角定理→∠ＤＰＣ＝２ａ
最後に△ＰＤＣの内角から、∠ＰＤＣ＝180－30－２ａ＝150－２ａ°
ア
（２）①
△ＡＢＤ≡△ＡＰＤの証明。
共通辺ＡＤ。
仮定より、∠ＢＡＤ＝∠ＰＡＤ（●）
ＡＤ//ＰＱの同位角→二等辺ＤＱＰの底角→錯角とつなげ、∠ＡＤＢ＝∠ＡＤＰ（×）
１辺と両端角が等しくので合同。
②
△ＡＢＤ＝③、△ＣＰＤ＝②とする。
前問の合同から、△ＡＰＤ＝③
△ＡＰＤ：△ＣＰＤ＝ＡＰ：ＰＣ＝３：２
ＡＤ//ＰＱより、△ＰＱＣ∽△ＡＤＣ→ＰＱ：ＡＤ＝２：５
仮定からＤＰ＝ＤＱ、合同の対応する辺でＤＰ＝ＤＢ
→ＤはＢＱの中点である。
今度は△ＢＤＲ∽△ＢＱＰに注目して、ＲＤ＝２÷２＝１
ＡＲ＝５－１＝４
ＡＲ：ＲＤ＝４：１
お…４、か…１
＠別解＠
△ＡＢＤ：△ＡＤＣ＝ＢＤ：ＤＣ＝３：５
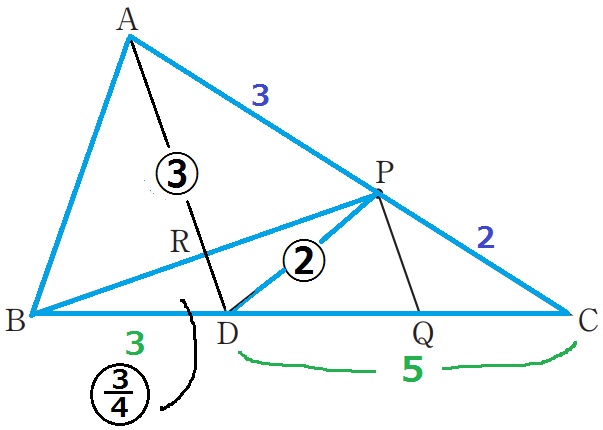
今度は、ＡＰ：ＰＣ＝△ＡＢＰ：△ＣＢＰ＝③：②と面積比を捉えなおす。
△ＤＢＰ＝②×３/８＝〇３/４
△ＡＢＰ：△ＤＢＰ＝ＡＲ：ＲＤ（高さの比）＝③：〇３/４＝４：１
大問５（空間図形）
（１）
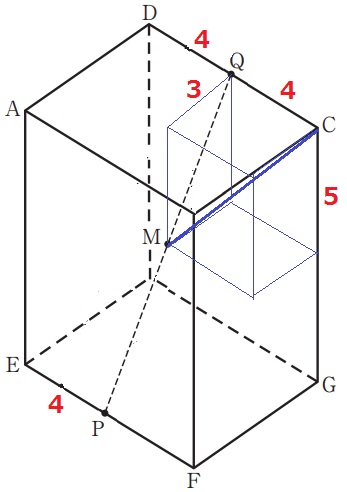
４秒後のＰはＥＦの、ＱはＣＤの中点にある。
ＰＱの中点Ｍは直方体の縦・横・高さの中点→直方体の中心。
ＭＣは１辺が３ｃｍ、４ｃｍ、５ｃｍの直方体の対角線だから、
ＭＣ＝√（３2＋４2＋５2）＝５√２ｃｍ
き…５、く…２
（２）
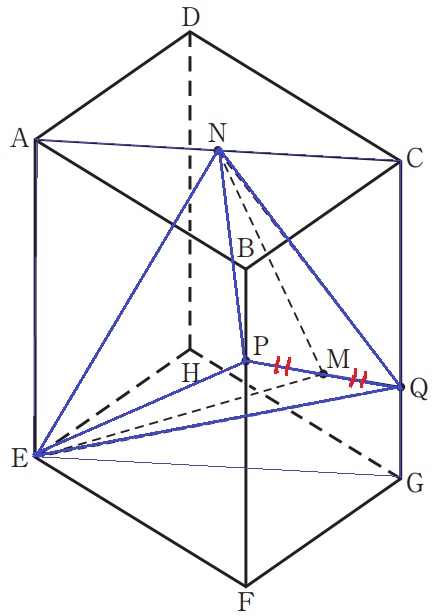
求めたいのは三角錐Ｍ―ＥＱＮだが、辺ＢＦ上にあるＰの方がＭより求めやすい。
そこで、ＰＭ＝ＭＱから三角錘ＭーＥＱＮ＝三角錘ＰーＥＱＮ÷２で求積する。
Ｅ・Ｎ・Ｑは面ＡＥＧＣ上にある。
三角錘ＰーＥＱＮの底面である△ＥＱＮの面積を求める。
Ｑを通るＮＥに平行な線をひき、ＥＧとの交点をＲとする。
等積変形で△ＥＱＮ＝△ＥＲＮ
ここで、△ＡＥＮと△ＧＱＲに着目すると２角相等で∽。
ＡＥ：ＡＮ＝ＧＱ：ＧＲ＝２：１
ＲＧ＝３÷２＝1.5ｃｍ
△ＥＦＧは辺の比が３：４：５の直角三角形だから、ＥＧ＝10ｃｍ
ＥＲ＝10－1.5＝8.5ｃｍ
最後に三角錘の高さを計算する。
△ＡＢＣの面積を２通りで表すと、【８×６÷２＝10×？÷２】
？＝８×６÷10＝24/５ｃｍ
よって、求積すべき立体の体積は、8.5×10÷２×24/５÷３÷２＝34ｃｍ3
け…３、こ…４
大問１
（８）Ｅは円周上の点ではない→∠ＢＥＤは外角定理から求める。
∠ＡＤＥは二等辺ＡＣＤの頂角。底角を円周角の定理で移動させる。
また、二等辺三角形の３つの頂点が円周上にある場合、頂角と円の中心を結ぶと線対称が使える。
（９）円Ａと円Ｂは合同の円なので、対称の軸が直線ℓといえる。
大問２
（１）図にａ～ｄの位置を書いておくと間違えない。
（２）ｅ以外をｅを使って表す。ｎは１つ下の数を表すときに使う。
大問３
（３）四角形ＢＯＲＰが平行四辺形である点に気づきたい。
ＰＲ＝８、ＲＱをＰ座標の文字で表せば方程式が立てられる。
大問４
（２）きちんと等角をつなげられるか。
（３）シンプルで良い問題。
相似が逆方向に流れる感じが分割前期と似ている。
与えられた面積比から、ＡＰ：ＰＣか、ＢＣ上の辺の比が求められないか探る。
大問５
（１）なるべくここは取りたい。Ｍの位置さえわかれば馴染みのある公式。
（２）Ｐ―ＥＱＮに切り替えて、底面ＥＱＮの面積を出す。
解説では等積変形を使ったが、四角形ＡＥＧＣから周りの３つの三角形を引いても良い。
＠2023年度・都立解説＠
数学…平均57.6点 社会…平均55.6点 理科…平均59.4点 英語…平均62.8点
公立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント