2023年度　北海道公立高校入試問題過去問【数学】解説

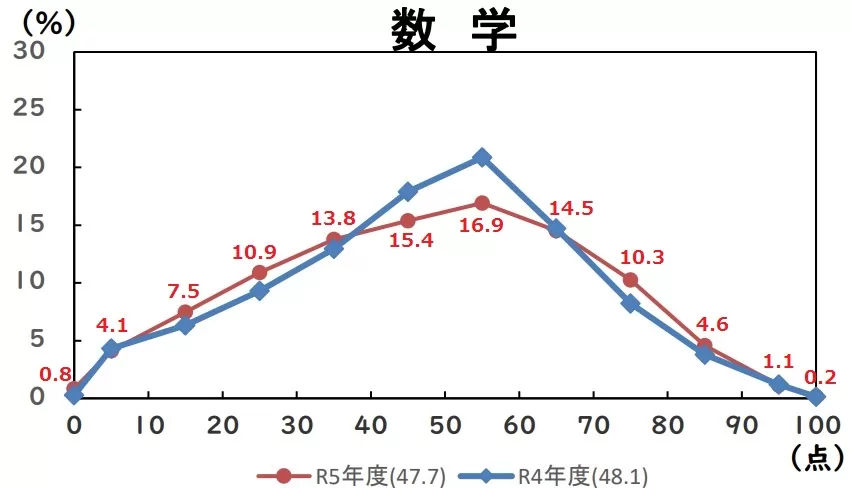
合格者平均47.4点（前年比；－0.2点）

問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）①　89.6％
９－（－５）
＝９＋５
＝14

②　75.2％
（－３）²÷１/６
＝９×６
＝54

③　84.1％
√２×√14
＝√28
＝２√７

（２）　84.8％
９本から４本ある偶数番号を引き当てればいい。
４/９

（３）　54.3％
（－１、６）→（３、２）
ｘが４増えると、ｙは４減少する⇒変化の割合は－１
ｘが１増えると、ｙは１減るから、６－１＝５

（４）　63.9％
６×６×π×□÷３＝132π
□＝11ｃｍ

（５）　48.5％
ｘ²－□ｘ＋14＝（ｘ－ａ）（ｘ－ｂ）
（－ａ）×（－ｂ）
＝ａｂ＝14
ａとｂは自然数だから、１×14、２×７のどちらか。

－□＝（－ａ）＋（－ｂ）
□＝ａ＋ｂ
→１＋14＝15、２＋７＝９
９、15

（６）　43.6％

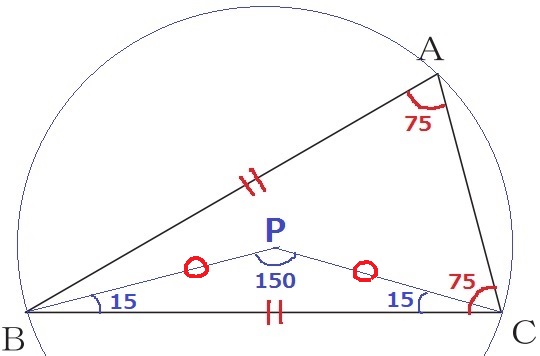
具体的な角が提示されているので、適当なＰを打って角を調べてみる。
仮定より、∠ＡＣＢ＝∠ＣＡＢ＝75°
二等辺ＰＢＣの内角で、∠ＢＰＣ＝180－15×２＝150°
75°×２＝150°、ＰＢ＝ＰＣから、∠ＢＡＣを円周角とする中心角が∠ＢＰＣにあたる。
すなわち、３点Ａ、Ｂ、Ｃを通る円の中心がＰである。
ＡＢ、ＢＣ、ＣＡいずれかの２本の垂直二等分線の交点がＰ。

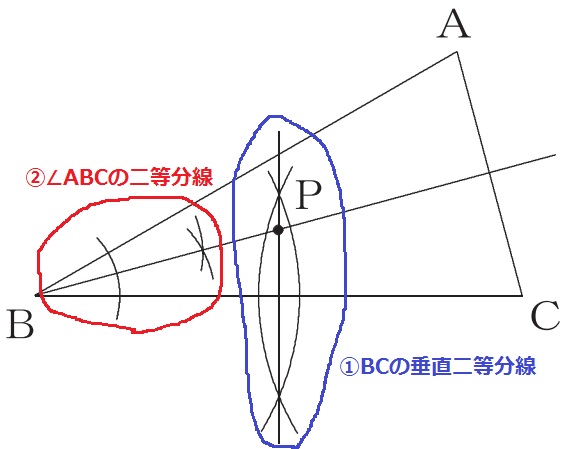
公式解答では①ＢＣの垂直二等分線と②∠ＡＢＣの二等分線をとっている。
∠ＡＢＣ＝30°を２等分すると∠ＰＢＣ＝15°
二等辺三角形の頂角を二等分する線は、底辺ＡＣの垂直二等分線と同じである。

大問２（整数）

（１）　81.4％
和が５の倍数にならない反例を挙げる。
左上４マスで、ａ～ｄの順で数字をあてはめると、
１＋２＋２＋４＝９で５の倍数にならない。
ア…１、イ…２、ウ…２、エ…４、オ…９
*他にも正答例がたくさんある。

（２）　24.5％！

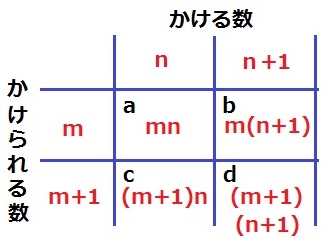
ａのかけられる数がｍ、かける数がｎ。
ａ＝ｍｎ、ｂ＝ｍ（ｎ＋１）、ｃ＝（ｍ＋１）ｎ、ｄ＝（ｍ＋１）（ｎ＋１）

ａ＋ｂ＋ｃ＋ｄ
＝ｍｎ＋ｍ（ｎ＋１）＋（ｍ＋１）ｎ＋（ｍ＋１）（ｎ＋１）
＝４ｍｎ＋２ｍ＋２ｎ＋１
＝（２ｍ＋１）（２ｎ＋１）
＝｛ｍ＋（ｍ＋１）｝｛ｎ＋（ｎ＋１）｝
（かけられる数の和）×（かける数の和）になっている。
ア…ｍ（ｎ＋１）、イ…（ｍ＋１）ｎ、ウ…（ｍ＋１）（ｎ＋１）
エ…ｍ、オ…ｍ＋１、カ…ｎ、キ…ｎ＋１

（３）　9.8％!!

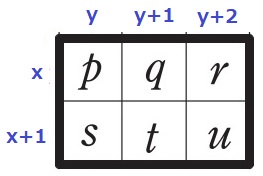
かけられる数の和…ｘ＋（ｘ＋１）＝２ｘ＋１
かける数の和…ｙ＋（ｙ＋１）＋（ｙ＋２）＝３ｙ＋３＝３（ｙ＋１）
その積は、３（２ｘ＋１）（ｙ＋１）＝162
（２ｘ＋１）（ｙ＋１）＝54

ここで偶奇判定で絞り込む。
２ｘは偶数だから、２ｘ＋１は奇数。
54は偶数なので（奇）×（偶）＝（偶）である。
→ｙ＋１は偶数。
また、２ｘ＋１は連続する２つの整数和なので３以上である。

（２ｘ＋１）【奇】×（ｙ＋１）【偶】の組み合わせは、
３×18＝９×６＝27×２の３通りである。
ここからどう絞るかですが…問題文の題材がかけ算の九九の表で、
図１は９×９の表しかないから、１桁×１桁の９×６になると考えるしかない。
２ｘ＋１＝９
ｘ＝４
ｙ＋１＝６
ｙ＝５
ｘ＝４、ｙ＝５
２桁以上の掛け算を考えた生徒はドンマイです(;´･ω･)

大問３（関数）

（１）　65.2％
ｙ＝２ｘ²にｙ＝８を代入。
８＝２ｘ²
ｘ＝±２
ＡとＢはｙ軸に関して対称なので、それぞれのｘ座標は２、－２。
ＡＢの距離は、２－（－２）＝４

（２）　25.1％！
答案では計算過程も書く。
ｙ＝ａｘ²において、ｘの値がｐ→ｑに増加するときの変化の割合はａ（ｐ＋ｑ）。
また、一次関数の変化の割合は傾きで表される。ｙ＝ｘ＋１の変化の割合は１。
ａ（１＋３）＝１
ａ＝１/４

（３）①　10.8％！

ｙ＝１/３ｘ²にｘ＝３を代入、Ａ（３、３）
ｙ＝－３ｘ²にｘ＝１を代入、Ｃ（１、－３）

Ｐ（ｔ、３）
ＰＱは原点Ｏを通り、かつＰとＱはｙ座標が共通するので原点Ｏについて対称関係である。
Ｑ（－ｔ、－３）

②　2.9％!!
直線ＰＱが台形ＡＢＣＤの面積を２等分する理由を説明する。

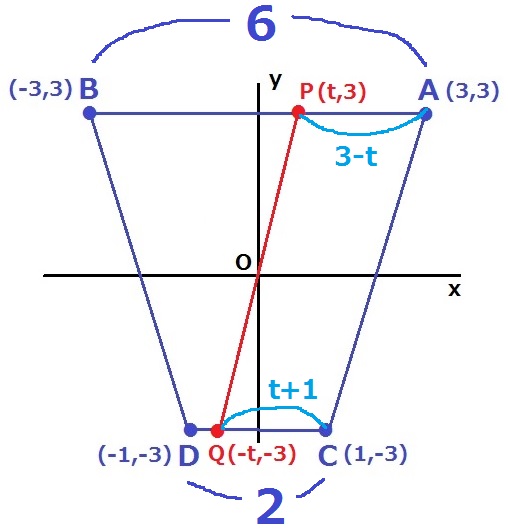
台形ＡＢＤＣの上底ＢＡ＝６、下底ＤＣ＝２の和が８だから、
台形ＡＰＱＣの上底ＰＡ＋下底ＱＣ＝８÷２＝４になればいい。
ＰＡ＋ＱＣ＝（３－ｔ）＋｛１－（－ｔ）｝＝４
したがって、直線ＰＱは台形ＡＢＣＤの面積を２等分する。
＠＠

公式解答ではきちんと面積を求めている。

大問４（平面図形）

（１）　67.1％
仮定から、∠ＤＡＣ＝35°
二等辺ＡＤＣの内角より、∠ＡＤＣ＝180－35×２＝110°

（２）①　44.9％
２つの証明を比較する。

【悠斗】
弧ＡＣに対する円周角と対頂角から、２角相等で△ＡＢＤ∽△ＣＥＤ
【由美】
弧ＡＣに対する円周角と仮定から、２角相等で△ＡＢＤ∽△ＡＥＣ
ア…弧ＡＣ、イ…円周角、ウ…２組の角が等しい

②　9.8％!!
△ＡＢＥ≡△ＡＤＣの証明。
公式解答では正答例が３つも紹介されている( Д ) ﾟ ﾟ

おススメというより、一番思いつきやすいのは正答例１。
弧ＡＢの円周角（×）→△ＡＢＥと△ＡＤＣの残りの角から１辺と両端角が等しい。
正答例２では由美の△ＡＢＤ∽△ＡＥＣを利用している。
対応する辺の比は等しく、ＡＢ＝ＡＤからＡＥ＝ＡＣがいえる。合同条件は２辺夾角。

正答例３はかなり迂回している(;^ω^)
先ほどの由美の考えからＡＥ＝ＡＣを指摘したうえで、
悠斗の△ＡＢＤ∽△ＣＥＤを用いて、同様に対応する辺とＡＢ＝ＡＤからＣＤ＝ＣＥ。
△ＣＤＥは二等辺三角形である。
さらに、仮定の等角●を円周角で移動→底角が等しく、△ＢＥＣは二等辺三角形。
ＢＥ＝ＥＣ＝ＤＣから、△ＡＢＥと△ＡＤＣの３辺が等しく合同。

大問５（データの活用）

（１）　68.8％
度数を合計してもよいが、累積度数の方がやや早い。
1972年において25℃未満が23日だから、25℃以上は62－23＝39日
同様に、2021年では62－19＝43日
夏日の差は、43－39＝４日
ア…39、イ…43、ウ…４

＠余談＠
最高気温25℃以上…夏日
30℃以上…真夏日
35℃以上…猛暑日
40℃以上…酷暑日　←NEW
正確には、昨年の2022年に日本気象協会が提言した新たな名称であり、
現段階では気象庁は採用していない。
ちなみに、30℃以上の夜間は『超熱帯夜』が選ばれたそうな( ´д)ﾋｿ(´д｀)ﾋｿ(д｀ )

（２）①　33.5％

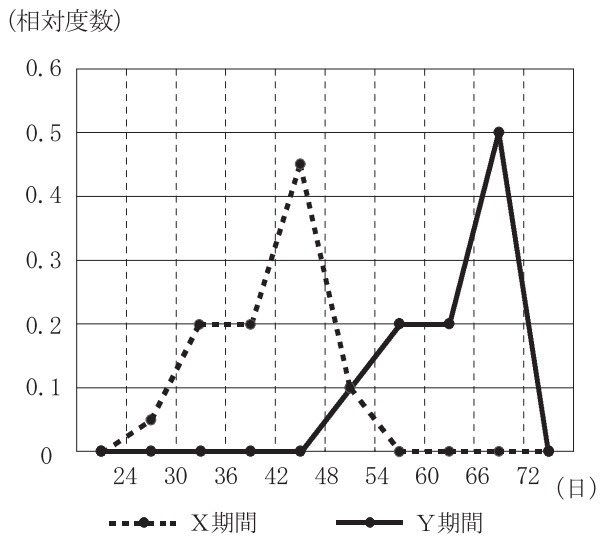
Ｙ期間の相対度数の度数折れ線を描く。
Ｘ期間のように階級値（目盛りの中央）にプロットする。

②　26.7％！
説明問題。
Ｘ期間は20年間、Ｙは10年間と調査期間（度数の合計）に差があるので、
割合である相対度数で比較した。

③　10.8％！
ラストも説明問題であった。
①のグラフを比較すると、２つのグラフは形が似ており、
全体的にＸ期間はＹ期間の左側に寄っているので、
50年くらい前の方が今より夏日が少なく、涼しかったといえる。
ウ