問題PDF
次の条件を満たす図形を定規のみを用いて作図しなさい。
ただし、定規は直線をかくためだけに使用し、作図に使用した直線は消さずに残しなさい。
(1)
下の図のように、中心をOとする円Oと、円Oの周上に点Aがあります。
Aを頂点の1つとする長方形を作図しなさい。ただし、定規の使用回数は6回までとします。

(2)
下の図のように、中心をOとする円Oと、円Oと2点で交わっている円Pがあります。
円Pの中心Pを作図しなさい。
ただし、定規の使用回数は6回までとし、作図したPの位置にPをかきなさい。

@解説@
(1)

4つの頂点が同一の円周上にあり、対角線が中心Oで交わるとき。
半径は等しい。
→直径にあたる対角線の長さは等しく、かつ対角線が各々の中点で交わる。
このような性質をもつ四角形は長方形か正方形しかない。
(正方形は特別な長方形)
@@
10cmの針金が2本ある。
真ん中5cmでクロスさせて、交点を固定したまま針金を好きな角度で回すと、
2本の針金の両端の4点を結んだ四角形は、いつでも長方形になる。

角度でも説明がつく。長方形の1つの内角は90°
赤線は2辺とあいだの角が等しいので、合同な二等辺三角形。
水色も同様で合同な二等辺。(●+×)×4=360
●+×=90°

①直線OAを引く。
②Oを通る適当な直線を引く。
③2直線が円周と交わる4点を結ぶ。
@図形の性質@
中学2年生で習う内容です。
●平行四辺形
【定義】
2組の対辺がそれぞれ平行である四角形。
【性質】
①2組の対辺は等しい。
②2組の対角も等しい。
③対角線はおのおのの中点で交わる。
以下の図形は、平行四辺形の性質を兼ね備える。
●長方形
【定義】4つの角が等しい四角形。
【性質】対角線の長さが等しい。
●菱形
【定義】4つの辺が等しい四角形。
【性質】対角線が垂直に交わる。
●正方形
【定義】4つの角と4つの辺が等しい四角形。
【性質】対角線の長さが等しく、垂直に交わる。
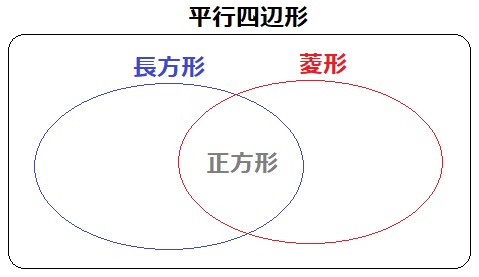
ベン図で関係性をあらわすと、このようになる。
長方形と菱形は特別な平行四辺形、正方形は特別な長方形・菱形。
(2)
前問では中心をOとし、4つの頂点が円周上にある長方形を描いた。
逆に、4つの頂点が円周上にある長方形を描けば、円の中心が決定できるかもしれない。

O以外で使える点は2円の交点●
●とOを直線で結ぶと、円Oの円周上に4点ができる。
これらを結ぶと長方形になるが、直線の回数制限があるので引かない。

横線2本を延長して、右円の円周上に4点をつくる。
長方形の対辺は平行で、中心Oは2本の平行線の真ん中の線上にある。
真ん中の線を対称の軸として図形全体が上下対称であり、この線上に右円の中心Pもある。
*(a・b)(c・d)(e・f)が対応する点。
efは真ん中の線と垂直に交わり、平行から四角形cdfeは内角すべて90°→長方形

長方形の対角線は各々の中点で交わる。
バッテンの交点がP


コメント