問題ＰＤＦ
〔図６〕のような一辺の長さが３ｃｍの正六角形ＡＢＣＤＥＦがあります。
点Ｐは辺ＡＢ上を動くことができ、点Ｑは辺ＣＤ上を動くことができます。
ＰＱを２：１に分ける点をＲとするとき、次の問いに答えなさい。
（１）
点Ｐが点Ａに止まっていて、点Ｑが辺ＣＤ上を点Ｃから点Ｄまで動くとき、
点Ｒの動く線の長さを求めなさい。
（２）
点Ｑが点Ｃに止まっていて、点Ｐが辺ＡＢ上を点Ａから点Ｂまで動くとき、
点Ｒの動く線の長さを求めなさい。
（３）
点Ｐが辺ＡＢ上を、点Ｑが辺ＣＤ上をそれぞれ自由に動くとき、
点Ｒの動くことができる範囲を、〔図７〕の例のように解答用紙の斜線で示しなさい。
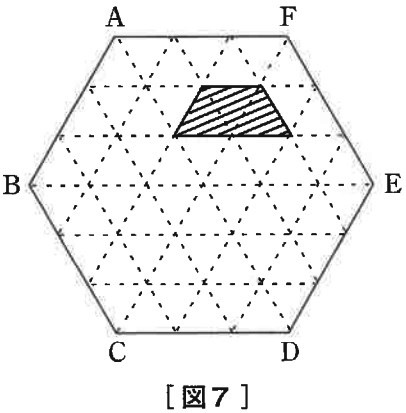
（４）
（３）で求めた範囲の面積は、正六角形ＡＢＣＤＥＦの面積の何倍になりますか。
（５）
点Ｒが（３）で求めた範囲を動くとき、正三角形ＥＦＲの面積が最も小さくなるのは、
三角形ＥＦＲの面積が、正六角形ＡＢＣＤＥＦの面積の何倍になるときですか。
＠解説＠
（１）
ＣＤ＝３ｃｍなので、３×２/３＝２ｃｍ
（２）
先ほどと比が違うので注意。
３×１/３＝１ｃｍ
（３）
範囲の問題はどこが端になるかを考える。
Ｐ－Ｑの組み合わせが、Ａ－Ｃ、Ａ－Ｄ、Ｂ－Ｃ、Ｂ－Ｄの場合を図示する。
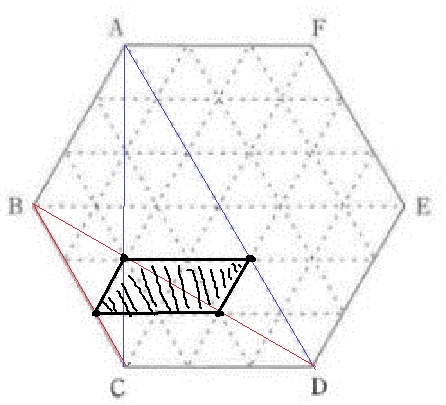
それぞれ２：１に内分する４つの点を囲うと平行四辺形になる。
この範囲が答え。
（４）
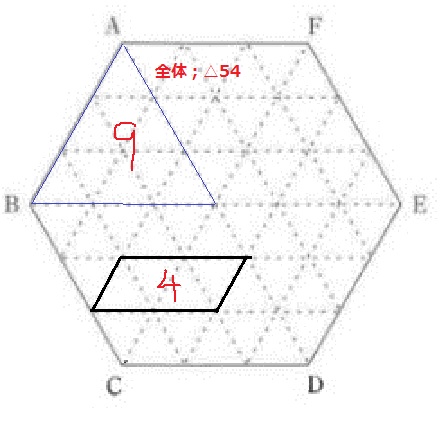
正三角形の数を数える。平行四辺形の中に４個。
全体は青いところが９つなので、それを６倍した54個。
４/54＝２/27倍
（５）
△ＥＦＲの面積が最も小さい。
→Ｒは平行四辺形の右上にくる。
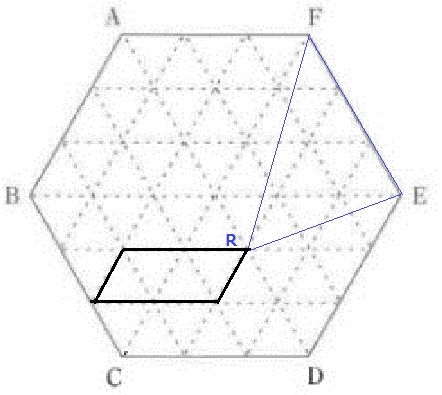
この三角形が正六角形の何倍かを求める。
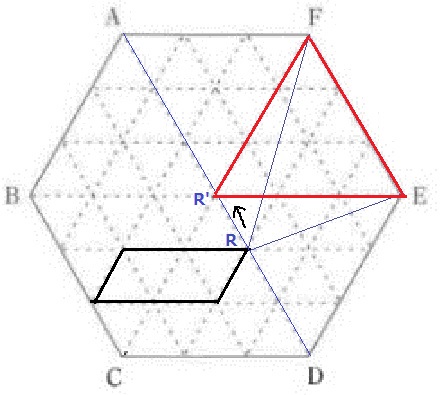
ＡＤに補助線。ＡＤ//ＦＥ
等積変形でＲの位置をズラす。
△ＦＲ’Ｅは正六角形の６分の１なので、答えは１/６倍。
難関中（算数科）解説ページに戻る
コメント