問題PDF
(1)
1周2.4kmの池の周りのA地点から、兄は歩いて、弟は走ってそれぞれ一定の速さで時計回りに進みました。兄は分速60mで進み、弟は兄より8分遅れて出発したところ、兄が1周する前に弟は兄に追いつきました。弟は兄に追いつくとすぐに逆方向に進み、A地点に戻ってきたときに兄と出会いました。弟の速さは分速何mでしたか。
(2)
同じ濃度の食塩水が容器Aに100g、容器Bに200g入っています。それぞれの容器の食塩水から同じ量の水を蒸発させたところ、容器Aの食塩水の濃度は容器Bの食塩水の濃度の1.5倍になりました。容器Aから何gの水を蒸発させましたか。
(3)
ある時刻に、長針と短針がぴったりと重なっていました。この時刻から100時間後までに、長針と短針がぴったり重なることは何回ありますか。ただし、初めにぴったりと重なっているときは、数えないものとします。
(4)

上の図のように、同じ大きさの正方形が縦に3個、横に5個ぴったりとくっついて並んでいます。
2つの点AとC、BとDを結んだとき、図の角アの大きさは何度ですか。
@解説@
(1)
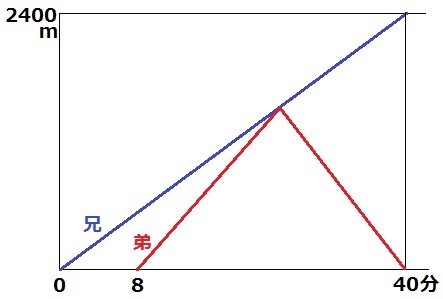
周回なので上下のボーダーラインはA地点で同じ。
兄は、2400÷60=40分でA地点に着く。(弟も同時刻にAに着く)
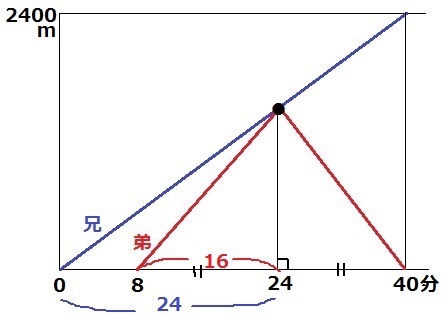
速度は一定なので、弟の赤線は二等辺三角形。
弟が出発してから、(40-8)÷2=16分後に兄に追いついた。
この距離を兄は24分で歩いたので、時間の比は兄:弟=24:16=3:2
速さは逆比で兄:弟=②:③
弟の速さは、60×③/②=毎分90m
(2)
濃度の比は、A:B=1.5:1=③:②

△は塩、□は蒸発させた水。
はじめのAとBの濃度は等しかったので、△/100=(2×△)/200である。
各々の食塩水から□gの水を蒸発させたときの濃度は上図の等式になる。

AとBの分子を△に統一すべく、Bの両辺を÷2して右辺を①にする。
分子が同じだと分母の比は逆比。
すなわち、100-□:200-□=①:③
差の100が②にあたるので、①=50g
100-□=50
□=50g
(3)
【1日で長針と短針が重なるのは22回】と聞いたことはあるはず。
スタートの0時00分の重なりを除外すると、最初の0時台は重なりがない。
1時台に1回、2時台に1回…11時台は次の12時00分に重なる。
12時間で11回の重なりだから、24時間では22回重なる。
48時間では44回、72時間では66回、96時間では88回重なる。
96時間後ちょうどにピッタリ重なるので、96時台は新たな重なりはなし。
97~99時台に1回ずつ重なる。(計3回)
99時台の重なりから100時間後までは1時間もないので重なりなし。
88+3=91回
(4)
もはや中学受験の世界では定番問題で、豊島岡志望であれば刹那で解ける。

下にもう1行マスを追加する。
ACは、縦1横4の長方形の対角線。
同じ対角線をBからひき、終点をEとする。
ACとBEは平行。同位角で∠アを∠DBEに移す。

つづいて、DEに補助線。
DEは縦4横1の長方形の対角線で、BE=DE

合同である青線の直角三角形で角度を調査。
●+×=90°より∠BED=90°
△BDEは直角二等辺三角形だから、∠ア=45°



コメント