問題ＰＤＦ
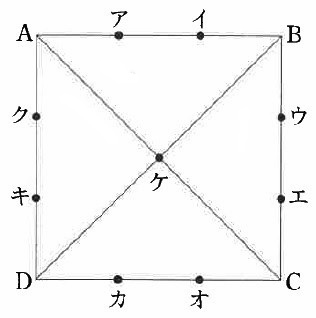
１辺が12ｃｍの正方形ＡＢＣＤにおいて、下の図のように、
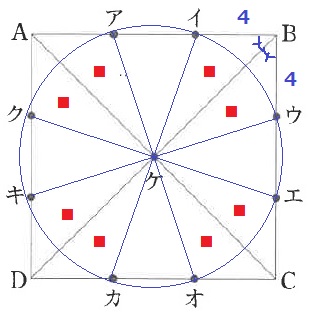
正方形の辺を３等分する点ア、イ、ウ、エ、オ、カ、キ、クとします。
また、正方形の２本の対角線が交わる点を点ケとします。
（１）
３点イ、エ、ケを結んでできる三角形の面積は〔 〕ｃｍ2です。
（２）
点ア、イ、ウ、エ、オ、カ、キ、クの８個の点をすべて通る円の面積は〔 〕ｃｍ2です。
＠解説＠
（１）
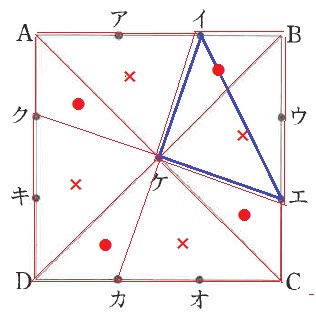
△イケエは、四角形イケエＢから△イエＢを引けばいい。
四角形イケエＢを△イケＢ（●）と△Ｂケエ（×）に分割すると、他の場所にも●と×があらわれる。
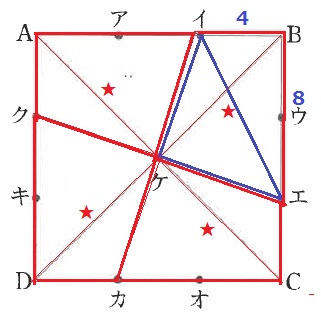
●と×をあわせて★にすると、四角形イケエＢの面積は正方形の４分の１とわかる。
△イケエ＝12×12÷４－４×８÷２＝20ｃｍ2
＠別解＠
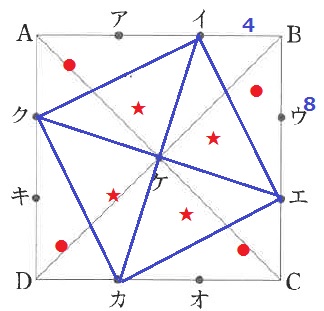
↑この分割でも可。
（12×12－４×８÷２×４）÷４＝20ｃｍ2
（２）
△イケＢと△ウケＢは、イＢ＝ウＢ＝４ｃｍ、∠イＢケ＝∠ウＢケ＝45°、
共通辺ケＢから２辺とあいだの角が等しく合同。
対称性から合同図形が８個見つかる。
ケから伸びる８本の線分の長さはすべて等しい→イケの長さは円の半径。
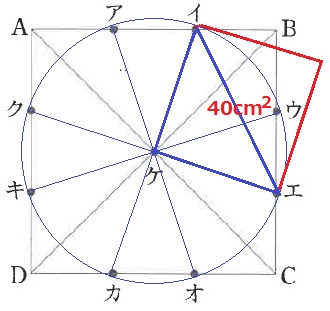
半径イケがわからなくても、正方形の面積から半径×半径はわかる。
40×3.14＝125.6ｃｍ2
難関中（算数科）解説ページに戻る
コメント