2019年度　専修大学松戸中学過去問【算数】大問６解説

問題ＰＤＦ
下の図は、１辺の長さが12ｃｍの立方体と１辺の長さが６ｃｍの立方体を組み合わせた立体です。
この立体を３つの点Ａ、Ｂ、Ｃを通る平面で切断して、２つの立体に分けました。
このとき、次の各問いに答えなさい。

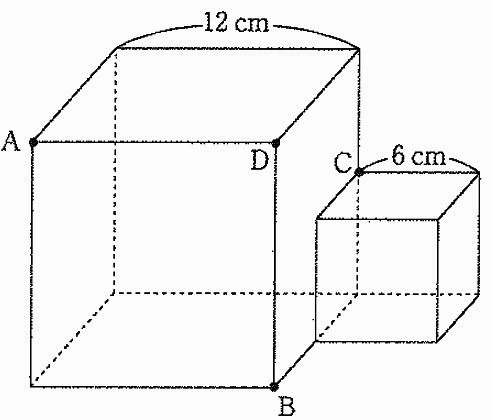
（１）
切断面はどのような形になりますか。
下のア～クの中から最も近いものを選びなさい。

（２）
２つに分けられた立体のうち、頂点Ｄをふくむ方の立体の体積は何ｃｍ³ですか。

＠解説＠
（１）
切断面の作図。
ＡＢはつながるとして、Ｃの扱いに困る。
ポイントは平行線。

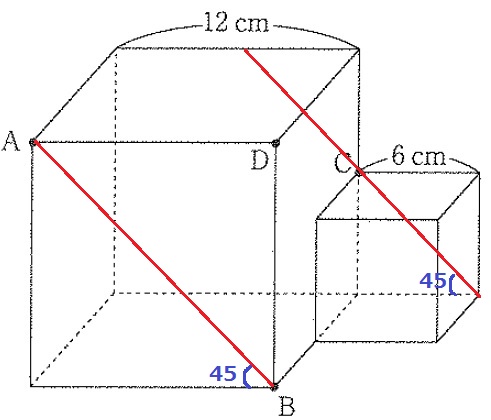
断面では対辺が平行なので、ＡＢの45度線がうしろにもできる。
Ｃを通過するように45度線をひく。

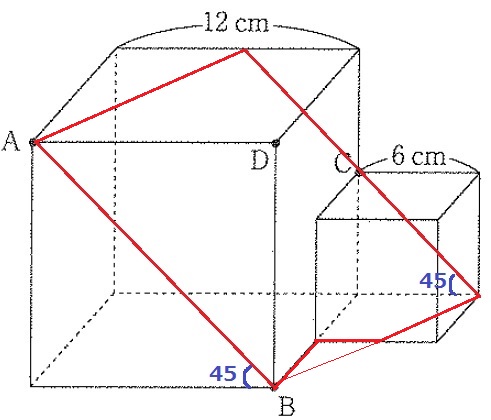
もう１つの対辺も平行線。
すると、断面は右下にクボミのある平行四辺形となる→カ

（２）
形がわかっても、やや出しにくい(;`ω´)
まずは長さを認定する。

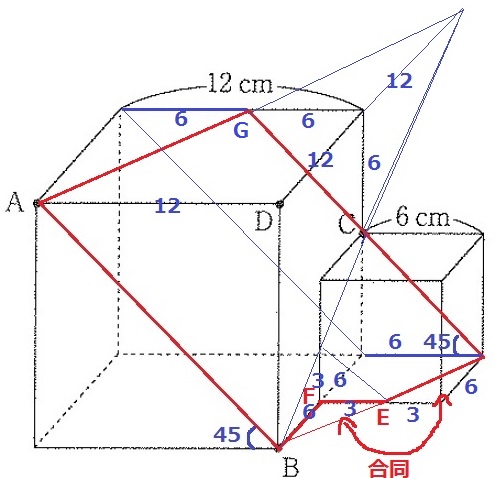
右下の三角形に注目。
ＢＦ＝６ｃｍから２つの三角形が合同。
ここからＥは小さい立方体の辺の中点にある。

次に、うしろの６ｃｍ（青線）を左上に平行移動する。
Ｇは大きい立方体の辺の中点にあるとわかる。

延長線をひいて２つの三角錐を作成。
小さい三角錐と大きい三角錐の相似比は１：２。
角錐台と三角錐の体積比は７：８。

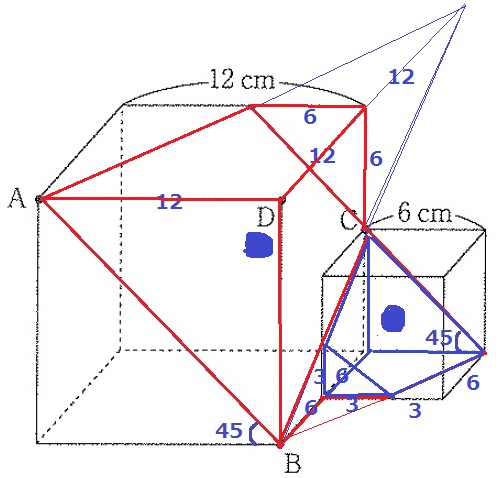
よくみると、角錐台●は同じ形で相似！
小さい立方体の後ろ（青の角錐台）は、６×６÷２×12÷３×７/８＝63ｃｍ³
小さい立方体の手前は、６×６×６－63＝153ｃｍ³

大きい立方体の手前（赤の角錐台）は先ほどの青と相似。
相似比が１：２⇒体積比は１：８。
赤…63×８＝504ｃｍ³
したがって、Ｄを含む立体の体積は、153＋504＝657ｃｍ³