2017年度　群馬県公立高校入試【数学】解説

最後以外は基本～標準。
記述でどこまで説明すべきか、判断がやや難しいところがある。
ラストは図形のセンスが問われる。
問題はコチラから→ＰＤＦファイル

大問１（小問集合）

（１）
①３－（－４）＝３＋４＝７
②√６÷√２＝√３
③（２ｘ－ｙ）/３－（３ｘ＋２ｙ）/６
＝｛２（２ｘ－ｙ）－（３ｘ＋２ｙ）/６
＝（４ｘ－２ｙ－３ｘ－２ｙ）/６
＝（ｘ－４ｙ）/６

（２）
絶対値＝数直線上で原点０からの距離。
０も整数！自然数ではない。
－２、－１、０、１、２

（３）
（ａ－３）²＝ａ²－６ａ＋９

（４）
ｘ²－２５＝（ｘ＋５）（ｘ－５）

（５）
7.25以上7.35未満。7.35は含まないよ！
7.25≦ａ＜7.35

（６）
奇数＋偶数＝奇数
３通り×２通り＝６通り。調べてもできる。
全・・₃Ｃ₂＝１０通り　　６/１０＝３/５

（７）
一次関数の一般式ｙ＝ａｘ＋ｂに代入→連立
ａ＝－３、ｂ＝２　→ｙ＝－３ｘ＋２

（８）
一応、頂点は対応する順番で書いておこう。
（△ＡＣＭ≡）△ＢＤＭ
（使った合同条件）２組の辺とその間の角が等しい。

大問２（関数）

（１）１ｍ
*ｙ＝１/４ｘ²にｘ＝２を代入するだけ。

（２）
振り子の等時性に関する記述。公式解答参照
*ｙに１/４を代入してｘを求める。
ｘ＝１
１往復にかかる時間はＢ１秒、Ａ２秒なので、
Ａが１往復する間にＢは２往復する。
最後の部分まで丁寧に記述する。

大問３（整数）

（１）４
*右上すみは平方数になっている。

（２）（ｎ＋１）²
（ｎ番目＋1）の２乗

（３）ｎ＝８
ここも記述。
前問より、右上は（ｎ＋１）²
左下はｎ²の次だからｎ²＋１
これらを合計して2次方程式へ。
（ｎ＋１）²＋（ｎ^２＋１）＝１４６
ｎ＞０より、ｎ＝８→８番目

大問４（作図）

（１）公式解答参照
*ＡＢの垂直二等分線とＢＣの垂直二等分線の交点がＯとなる。
もちろん、ＡＣの垂直二等分線でも良い。３本のうち２本を選ぶ。
Ｏを中心にいずれかの点までを半径としてグルっと１周すれば、
△ＡＢＣの外接円ができる。

（２）前問の作図方法の仕組みを説明する。
公式解答をみると、垂直二等分線上にある→２点からの距離が等しいとしたうえで、
ＡＯ＝ＢＯ、ＢＯ＝ＣＯから、ＡＯ＝ＢＯ＝ＣＯとしている。
なぜ垂直二等分線上の点は２点からの距離が等しくなるかについての説明は不要。
合同図形からでも説明できる。
ＡＢの中点をＭ、ＢＣの中点をＮとし、
△ＡＯＭ≡△ＢＯＭ、△ＯＢＮ≡△ＯＣＮ。あとは対応する辺から同じ。
いずれにせよ、どこまで言及すべきかわからず、書きにくさはある。

大問５（図形の証明）

ア・・９０　イ・・ＡＥ　ウ・・ＡＨ
（証明の続き）
同じ長さに対する円周角は等しいので、
∠ＡＥＨ＝∠ＢＨＥ
錯角が等しいので、
ＥＡ//ＢＨ
*前半は誘導に従い、証明の続きを完成させる。千葉と同じ。
ア：弧ＡＢと弧ＥＨがともに円周の４分の１であるから、中心角は９０°となる。
ｲｳ：同じ長さの弧から、共通する間の弧をひけば残りの弧の長さも等しくなる。
平行の証明は、同位角か錯角が等しいことを指摘すればいい。
円周の長さが等しい＝円周角が等しい。ここから錯角が等しい→平行となる。

大問６（相似）

（１）３ｃｍ
*△ＯＢＣ内で中点連結定理。ＢＣ：ＰＱ＝２：１

（２）①５：１　　②５＋２√３３ｃｍ
*①△ＡＰＯと△ＡＰＢで三平方の定理。ＡＰ²で等式を作る。
ＯＰ＝ｘとおく。ＰＢ＝６√３－ｘ
（６√３）²－ｘ²＝６²－（６√３－ｘ）²
１２√３ｘ＝１８０
ｘ＝５√３　　ＯＰ＝５√３ｃｍ
ＰＢ＝６√３－５√３＝√３ｃｍ
したがって、ＯＰ：ＰＢ＝５√３：√３＝５：１
②前問の流れから△ＡＰＢ内で三平方。
ＡＰ＝√{６²－（√３）²｝＝√３３ｃｍ
同様に、ＱＤ＝√３３ｃｍ
ＰＱは前問の比から、△ＯＢＣ∽△ＯＰＧ
ＰＱ：ＢＣ＝５：６。よって、ＰＱ＝５ｃｍ
ＡＤ＝ＡＰ＋ＰＱ＋ＱＤ＝５＋２√３３ｃｍ

（３）１６ｃｍ
*やや難。
本問は角度の情報が与えられておらず、三平方が使えない。
とりあえず、展開図を書いて何が使えるか、図形とにらめっこする。
すると、△ＡＢＰが二等辺三角形のような気がしてくる。
視点を隣の二等辺三角形ＯＢＣに向けてみよう。

等しい角度に印をつけみてる。
△ＯＡＢは二等辺三角形。正四角錘なので△ＯＢＣと合同である。
ここでＡＤとＢＣは平行になる。
五角形ＯＡＢＣＤは合同な３つの二等辺三角形を３つ並べた図形で線対称の図形である。
糸を最短経路で巻きつけたということはＢＤは一直線。
ＢＣと平行でなければＡＤは傾いてしまい、
左右対称にはならないからＡＤ//ＢＣとなる。
（数学的にいえばＡとＤ、ＢとＣは対応する点なので、ＡＤとＢＣが対称の軸と直角で交わる。
→同位角が等しい→平行）
ＡＤ//ＢＣであるから、錯角から∠ＰＢＣ（青い○つけ忘れたところ）＝∠ＡＰＢ
２角が等しいことから△ＯＡＢ∽△ＡＰＢとなる。
△ＡＰＢも二等辺三角形なので、ＡＰ＝６ｃｍ（ＱＤ＝６ｃｍ）
残るＰＱは前問のように△ＯＢＣ∽△ＯＰＧ
辺の比から、６√３：６＝６：ＢＰ
ＢＰ＝２√３ｃｍ、ＯＰ＝６√３－２√３＝４√３ｃｍ
ＯＢ：ＯＰ＝６√３：４√３＝３：２
△ＯＢＣ∽△ＯＰＧから、ＰＱ＝６×２/３＝４ｃｍ
ＡＤ＝ＡＰ＋ＰＱ＋ＱＤ＝６＋４＋６＝１６ｃｍ

＠別解＠
２角が等しいことから△ＯＡＢ∽△ＡＰＢとなる。
↑ここの説明ですが、二等辺三角形の２つの底角以外でも説明できます。
合同な３つの二等辺三角形なので、ＯＡ＝ＯＢ＝ＯＣ＝ＯＤ
ということは、４点ＡＢＣＤはＯＡを半径とする円の円周上にあります。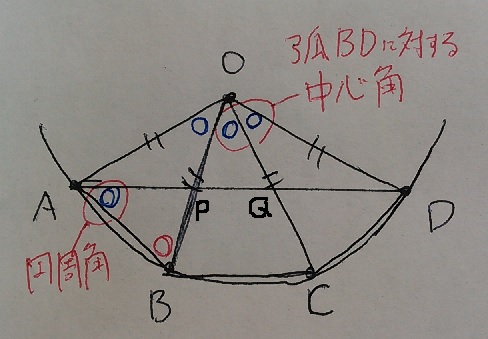
弧ＢＤに対する中心角∠ＢＯＤ＝○○
弧ＢＤに対する円周角は∠ＢＡＤとなり、円周角の定理から○１個分です。
すなわち、二等辺三角形の頂角である∠ＡＯＢと∠ＢＡＰが等しくなります。
あとは共通角である∠ＯＢＡをもってくれば、２角を指摘できますね。
公立高校入試解説ページに戻る