平均46.9点(前年比;+0.9点)
問題はこちら→リセマムさん
出題範囲の除外は標本調査。
大問1(小問集合)
(1)
12÷(-4)
=-3
(2)
√3×√8
=√3×2√2
=2√6
(3)
(x-4)(x-5)
=x2-9x+20
(4)
x2-5x+3=0
解の公式を適用して、x=(5±√13)/2
(5)
1桁の偶数は2・4・6・8の4枚。
♦♥♣♠に4枚ずつあるから、4×4=16枚
確率は、16/52=4/13
(6)
3~6冊の度数は、30-(7+5+3+2+1)=12冊
12÷30=12/30=4/10=0.4
(7)
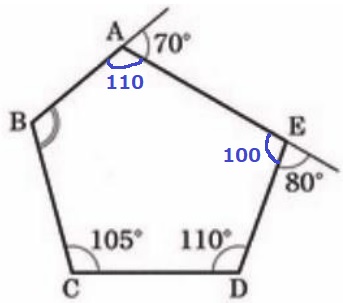
五角形の内角の和は540°
*n角形の内角の和は180(n-2)°
540-(110+100+110+105)
=540-425
=115°
(8)
y=5/2x+aに(x、y)=(4、3)を代入。
3=5/2×4+a
a=-7
y軸との交点⇒切片は(0、-7)
(9)
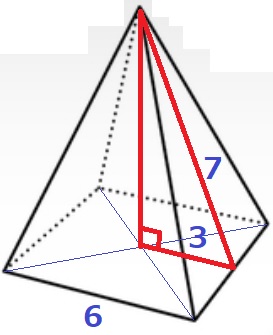
四角錐の高さは、√(72-32)=2√10cm
体積は、6×6×2√10÷3=24√10cm3
(10)
336を素因数分解。
336=24×3×7
336をnで割ったとき、残った素因数が偶数個になれば平方数になる。
2の素因数は4つあるが、3と7は1つずつしかない。
3×7=21で336を割れば、商は24=42=16(平方数)になる。
21
大問2(方程式)
(1)
みきさんは玉ねぎをx袋、じゃがいもをy袋とした。
袋の数で等式。
x+y=91
売上金額の合計で等式。
190x+245y=19380
ゆうさんは玉ねぎをx個、じゃがいもをy個とした。
袋の数で等式。
袋の数=(野菜の総数)÷(1袋あたりの野菜の個数)
x/3+y/6=91
売上金額の合計で等式。
それぞれの袋の数に190円と245円をかければいい。
190/3x+245/6y=19380
ア…x+y、イ…190x+245y
ウ…x/3+y/6、エ…190/3x+245/6y
(2)
前問の連立を解く。
以下、みきの方法。
x+y=91 …①
190x+245y=19380 …②
②-①×190をすると、55y=2090
y=38
①に代入、x=53
文字は袋の数であることに注意!
玉ねぎが53袋、じゃがいもが38袋だから、
玉ねぎは、3×53=159個
じゃがいもは、6×38=228個
玉ねぎ…159個、じゃがいも…228個
大問3(場合の数・平面図形)
(1)
Aの順番で場合分け。
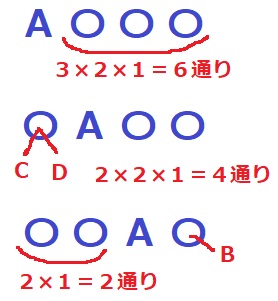
◆Aが1番目のとき、Bはどこでも良い。
残り3つは順列の考えで、3×2×1=6通り
◆Aが2番目のとき、1番目を先に決めるとCかDの2通り
2×2×1=4通り
◆Aが3番目のとき、4番目はBが確定。
残り2つは、2×1=2通り
◆Aが4番目は無い。
12通り
(2)a
24×2×π×1/3=16πcm
b
扇形の半径しかわかっていない。
そこで、長方形の辺と扇形が関わるところを探す。
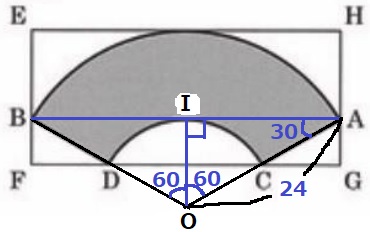
FG=BA
120°を活用する。
扇形の中心OからBAにむけて垂線をひき、交点をIとすると、
図形全体が左右対称ゆえ、∠IOA=120÷2=60°
△OIAの内角は30°—60°—90°で、辺の比が1:2:√3の直角三角形!
IA=24×√3/2=12√3cm
IはBAの中点だから、
FG=BA=12√3×2=24√3cm
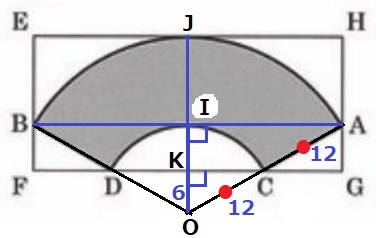
上図のように記号をつけると、EFの長さはJKにあたる。
IA//KCより、△OKCの辺の比も1:2:√3。
OK=12÷2=6cm
OJは扇形の半径24cmだから、EF=JK=24-6=18cm
EF…18cm、FG…24√3cm
大問4(関数)
(1)a
y=1/2x2にx=-4を代入。
y=1/2×(-4)2=8
b
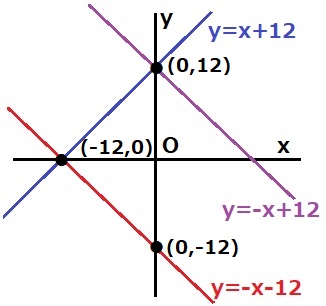
y=x+12をx軸について線対称⇒y=-x-12
(*y軸について線対称だとy=-x+12)
(2)a

y=1/2x2にx=2を代入して、P(2、2)
Qのy座標が2だから、これをy=x+12に代入して、Q(-10、2)

長方形を2等分すると、点対称にある2つの台形ができる。
2等分する直線とQPの交点をTとする。
SO=10、OR=2だから、QT=2、TP=10
(一方の台形は上底2下底10、他方の台形は上底10下底2で等積)
TからOは右に8、下に2ゆえ、傾きは-2/8=-1/4
y=-1/4x
b
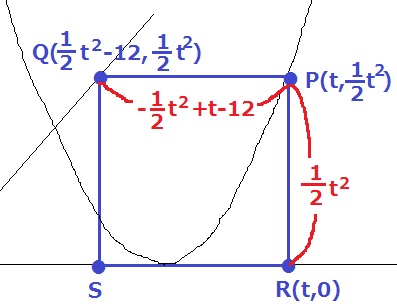
お決まりの手口。座標を文字で表して方程式に持ち込む。
放物線上にあるPのx座標をtとすると、P(t、-1/2t2)R(t、0)
Qのy座標が1/2t2だから、これをy=x+12に代入して、Q(1/2t2-12、1/2t2)
正方形は横と縦の長さが同じ。
PQ=t-(1/2t2-12)=-1/2t2+t+12
PR=1/2t2
-1/2t2+t+12=1/2t2
t2-t-12=(t+3)(t-4)=0
t=-3、4
PR=1/2t2だから、
Pのx座標が-3のとき、PR=1/2×(-3)2=9/2
Pのx座標が4のとき、PR=1/2×42=8
9/2、8
大問5(平面図形)
(1)

△DEFで外角定理。
∠DEF=∠DEG=a-90°
(2)
△ABD∽△DEBの証明。

すぐ見える。
直角+AD//BEの錯角→2角相等で∽
(3)

△ADBで三平方→BD=2√5cm
前問の相似を活用する。
△ABD∽△DEBより、BE=2√5×2√5/4=5cm
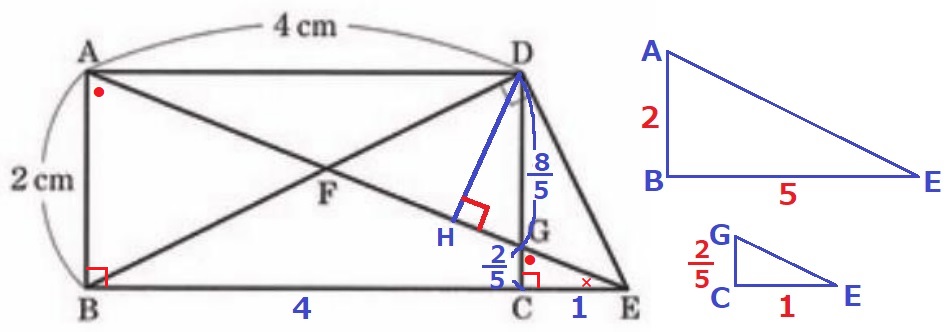
△ABEで三平方→AE=√29cm
AD//BEより、等積変形で△ABD=△AED=2×4÷2=4cm2
DHは△AEDの底辺をAEとしたときの高さだから、
DH=4×2÷√29=8√29/29cm
(4)
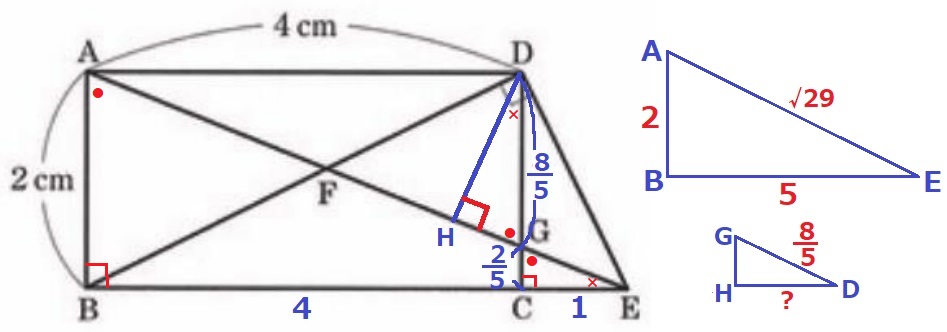
△ABE∽△GCEより、GC=2×1/5=2/5cm
DG=2-2/5=8/5cm

△BDCから△FDGを引く。
△ABF∽△GDFより、AF:FG=2:8/5=⑤:④
△ADF:△FDGの面積比も⑤:④だから、
〔△ADG⇒△FDG〕△FDGの面積は、4×8/5÷2×④/⑨=64/45cm2
四角形BCGFの面積は、2×4÷2-64/45=116/45cm2
●講評●
大問1
ここだけで配点が40点もある!
(9)見えなかったら立体図を書こう。
(10)割り算をすると素因数が消える。
大問2
2つのパターンを求める連立方程式は他県でも出てくる。
慣れていない方法でも立式できるようにしておきたい。
大問3
(1)樹形図で調べてもい良い。
(2)b扇形と長方形が関わる線分に狙いをつける。
大問4
(1)平行四辺形を2等分する直線は対角線の交点を通り、
上底と下底の和が等しく、2つの台形が点対称。
大問5
(1)∠DEG=∠DEFから、△DEFに目をつける。
(3)図はシンプルだが意外と数値が汚かった。DHはどういう線分か。
(4)△BDCは長方形の半分でサクッと求まるので、これから△FDGを引けばいい。



コメント