2022年度　神奈川県公立高校入試問題過去問【数学】解説

平均52.9点（前年比；－5.3点）

問題はコチラ→ＰＤＦファイル
2022年度・神奈川追試験（数学）の解説はコチラ。

大問１（計算）
大問２（小問集合）
大問３（小問集合２）
大問４（関数）
大問５（確率）
大問６（空間図形）

大問１（計算）

（ア）　97.3％
－６＋（－９）
＝－６－９
＝－15　【１】

（イ）　87.4％
－３/８＋２/３
＝７/24　【４】

（ウ）　89.5％
（３ｘ－ｙ）/４－（ｘ－２ｙ）/６
＝｛３（３ｘ－ｙ）－２（ｘ－２ｙ）｝/12
＝（９ｘ－３ｙ－２ｘ＋４ｙ）/12
＝（７ｘ＋ｙ）/12　【３】

（エ）　93.6％
18/√２－√32
＝９√２－４√２
＝５√２　【２】

（オ）　89.2％
（ｘ－２）（ｘ－５）－（ｘ－３）²
＝ｘ²－７ｘ＋10－ｘ²＋６ｘ－９
＝－ｘ＋１　【３】

大問２（小問集合）

（ア）　80.4％
0.2ｘ＋0.8ｙ＝１　…①
１/２ｘ＋７/８ｙ＝－２　…②

①を10倍して、２ｘ＋８ｙ＝10　…③
②を８倍して、４ｘ＋７ｙ＝－16　…④
③×２－④をすると、ｙ＝４
③に代入して、ｘ＝－11
ｘ＝－11、ｙ＝４　【１】

（イ）　92.3％
４ｘ²－ｘ－２＝０
解の公式を適用して、ｘ＝（１±√33）/８　【３】

（ウ）　78.4％
ａ＜０だから、上に凸のグラフ。
ｘ＝０のとき、最大値ｙ＝０
ｘ＝４のとき、最小値ｙ＝－４
－４≦ｙ≦０だから、ａ＝－４、ｂ＝０　【２】

（エ）　59.2％
求めたいＡ班をｘ人とすると、Ｂ班はｘ－５人。
Ａ班が並べたイス…３ｘ脚
Ｂ班が並べたイス…４（ｘ－５）脚
Ａ班がＢ班より３脚多かったので、等式を成り立たせるにはＡ班側を－３する。
３ｘ－３＝４（ｘ－５）
ｘ＝17
17人　【３】

（オ）　69.6％
対称式は、あらかじめ和と積を出しておく。
ｘ＋ｙ＝（√６＋√３）＋（√６－√３）＝２√６
ｘｙ＝（√６＋√３）（√６－√３）＝６－３＝３

ｘ²ｙ＋ｘｙ²
＝ｘｙ（ｘ＋ｙ）　←ここで代入。
＝３×２√６
＝６√６　【４】

大問３（小問集合２）

（ア）ⅰ　ａ…80.1％、ｂｃ…78.6％
△ＤＥＧ≡△ＤＣＨの証明。

仮定より、ＤＧ＝ＤＨ
二等辺三角形ＦＤＣの底角と、ＡＤ//ＢＣの錯角で∠ＡＤＣ＝∠ＤＣＦ
よって、∠ＥＤＧ＝∠ＣＤＨ

∠ＢＣＤの二等分線と錯角により、△ＤＥＣは二等辺三角形だからＤＥ＝ＤＣ
２辺とあいだの角が等しいので△ＤＥＧ≡△ＤＣＨとなる。
ａ…【３】、ｂ…【２】、ｃ…【２】

ⅱ　37.8％
思考力が試される良い問題です。

平行四辺形ＡＢＣＤより、対角は等しいから∠ＡＢＣ＝●
●をいじったら四角形ＣＦＤＥが平行四辺形になった。
平行四辺形になる条件はいろいろあるが、たぶん有名角だろうと想像する。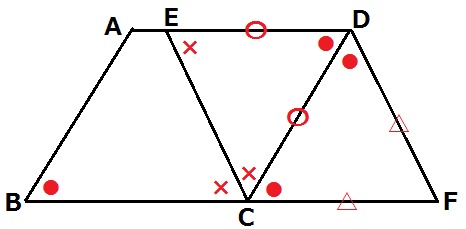
もし、●＝60°ならば二等辺三角形ＣＤＥより×＝60°となり、△ＣＤＥは正三角形。
∠ＦＤＣ（●）＝∠ＥＣＤ（×）＝60°で錯角が等しくなり、ＥＣ//ＤＦがいえる。
ＥＤ//ＣＦと合わせて２組の対辺が平行だから、四角形ＣＦＤＥは平行四辺形。
よって、∠ＡＢＣ＝60°　【４】

（イ）　25.4％！
こちらは悪問。
１年生の中央値（メジアン）を求める。
38人の中央値は19番目と20番目の平均で22～26の階級。
それぞれのヒストグラムの中央値を求めるが、しんどくてイライラする(*’ω’*)???? ????
こういうのは１度試せば良い話で、同じ作業をもう６回も要求するのは問題として不適である。

40人の中央値は20番目と21番目の平均。それぞれの中央値を含む階級は、
１が22-26、２が22-26、３が18-22、４が18-22、５が22-26、６が26-30です ???? ???? ????
（３と４については30回以上の生徒が少ないので、目分量でスキップ可）
２年生は１・２・５のいずれか。
30回以上の割合は、１年生が７/38、１が４/40、２が９/40、５が９/40。
２年生の方が小さいので、１が２年生。

３年生の最大値は34-38の階級にあるので、４・５・６のいずれか。
２年生の最頻値（モード）が26-30の階級だから５が外れる。
14回未満の割合は、１年生が４/38、４が６/40、６が４/40。
３年生の方が小さいので、６が３年生。
ⅰ…【１】、ⅱ…【６】

（ウ）　16.3％！
出しにくい。

ＢＣに補助線をひくと、四角形ＢＣＤＥは等脚台形。
錯角や弧ＢＣ・弧ＤＥに対する円周角を使うと、●はすべて等角で二等辺三角形が２つある。
外角定理より、●＝86÷２＝43°

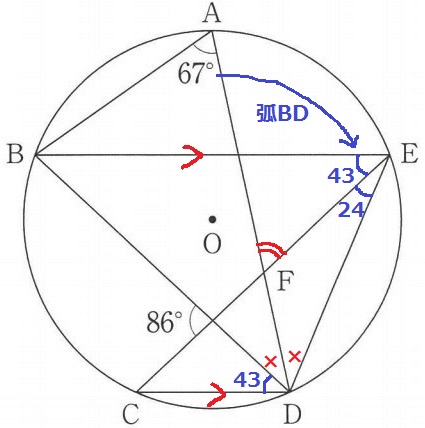
弧ＢＤに対する円周角で、∠ＢＥＤ＝67°
∠ＦＥＤ＝67－43＝24°
×の角度が知りたい。

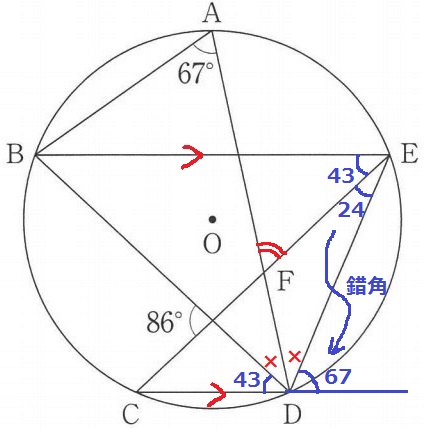
67°を錯角でおろすとわかりやすい。
×＝（180－43－67）÷２＝35°
最後に△ＤＥＦで外角定理→∠ＡＦＥ＝24＋35＝59°

（エ）　0.7％!!!
大問３からヘビー過ぎる。
思いつきにくいので後回し推奨です。

直径に対する円周角で、∠ＡＣＢ＝∠ＡＤＢ＝90°
同位角で、∠ＡＥＤ＝90°

ＡＥ：ＥＤ＝２：３を活用する。
長方形ＣＥＤＧを作成。
∠ＡＤＥ（×）＝90－∠ＦＤＢ
∠ＢＤＧ＝90－∠ＦＤＢ＝×
２角相等で△ＡＤＥ∽△ＢＤＧが導ける。
ＢＧ＝１×２/３＝２/３ｃｍ

ＣＢ＝３－２/３＝７/３ｃｍ
△ＡＦＥ∽△ＡＢＣで、ＥＦ＝７/３×２/３＝14/９ｃｍ

ＦＤ＝３－14/９＝13/９ｃｍ
△ＢＤＦの面積は、13/９×１÷２＝13/18ｃｍ²

大問４（関数）

（ア）　87.0％
ｙ＝ｘ＋３にｘ＝６を代入してｙ＝９
Ａ（６、９）
これをｙ＝ａｘ²に放り込むと、
９＝36ａ
ａ＝１/４　【２】

（イ）　74.6％

座標を確定していく。
Ｂはｙ軸についてＡと対称だから（－６、９）。
ｙ＝ｘ＋３にｘ＝－６を代入、Ｃ（－６、－３）。
ＤＯ：ＯＥ＝⑥：⑤より、Ｅ（５、０）

Ｃ（－６、－３）⇒Ｅ（５、０）は右に11、上に３移動するから、傾きｍ＝３/11
切片は三角形の相似を使って３×⑤/⑪＝15/11→切片ｎ＝－15/11
ⅰ…【３】、ⅱ…【５】

（ウ）　6.9％!!

△ＡＦＧと△ＡＥＧが等積なので、底辺の長さは等しい→ＦＧ＝ＧＥ
ＧはＥＦの中点。Ｇのｙ座標は９÷２＝4.5
これをｙ＝ｘ＋３に代入して、Ｇ（1.5、4.5）

ｘ座標に注目すると、Ｅから－3.5がＧ。Ｇからさらに－3.5でＦ（－２、９）。
ＢＦ：ＦＡ＝４：８＝１：２
△ＢＦＧ：△ＡＦＧ＝①：②
等積で△ＡＥＧ＝②

ｘ座標の差から、ＣＧ：ＧＡ＝7.5：4.5＝15：９＝５：３
△ＣＥＧ＝②×５/３＝〇10/３
よって、△ＢＧＦ：△ＣＥＧ＝①：〇10/3＝３：10

大問５（確率）

（ア）　76.9％
ＸとＹの面積が等しいということは、ＲはＰＱに中点にある。
ＰＲ：ＲＱ＝１：１
さいころの出目が同数になればいい。
（１、１）（２、２）…（６、６）の６通り。
全体が６×６＝36通りだから、確率は６/36＝１/６

（イ）　14.7％！
なんじゃこりゃ(;°;ω;°;)

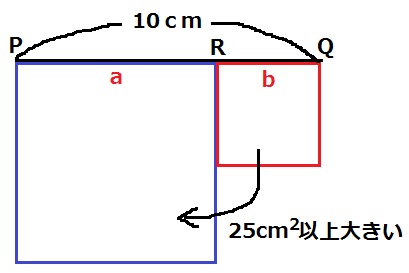
こういうことなんですけど、ａとｂは割合であって長さではない。。

１次不等式を使わせて頂きます( ˙ω˙ )

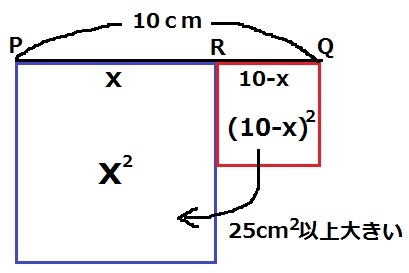
ＰＲ＝ｘｃｍ、ＲＱ＝10－ｘｃｍとする。
ｘ²－（10－ｘ）²
＝ｘ²－100＋20ｘｰｘ²
＝20ｘ－100≧25
ｘ≧6.25

ＰＲが6.25ｃｍ以上になれば条件に適する。
ＰＱの長さが10ｃｍなので、割合でいえば、6.25÷10＝５/８
ＰＲの割合が５/８（百分率でいえば62.5％）以上となる場合を調べる。

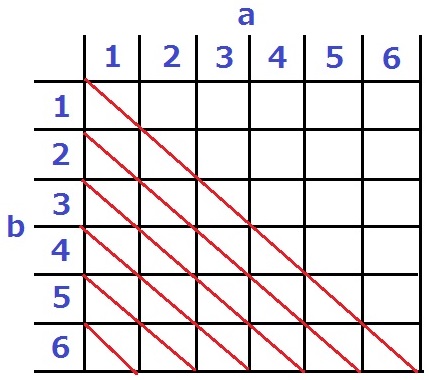
ａ＞ｂでないとダメなので、残りは15マス。

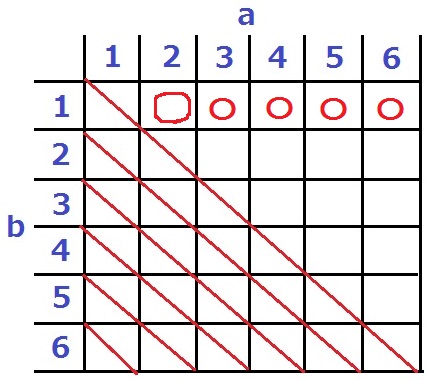
（ａ、ｂ）＝（２、１）で、ＰＲの割合は２/３（66.6％）だから〇。
右４つもすべて〇です。

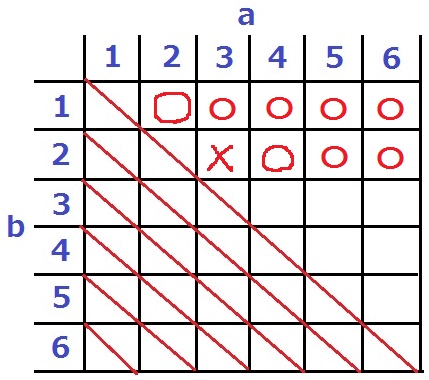
（３、２）ではＰＲの割合が３/５（60％）で不適。
（４、２）は先ほどの（２、１）と割合が同じだから〇。右２つも〇。

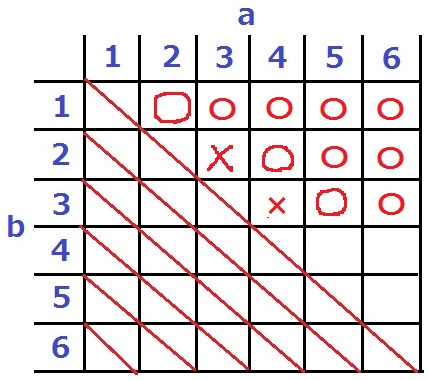
先に（５、３）を検証すると、ＰＲの割合がちょうど５/８で〇。
その左が×で、右が〇。

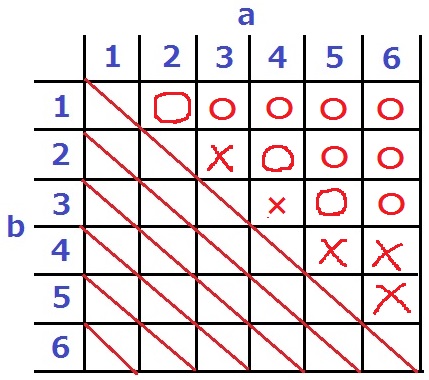
先ほどの（５、３）がちょうど５/８だったので、
（５、４）の５/９は計算するまでもなく割合が小さいとわかる×。
すると、左の（６、４）も自動的に×。下の（６、５）も連鎖して×。
合計10通り。
確率は10/36＝５/18

＠別解＠

Ｘの１辺は、10×ａ/（ａ＋ｂ）ｃｍ
Ｙの１辺は、10×ｂ/（ａ＋ｂ）ｃｍ
これらを２乗した差が25以上になる。

両辺を÷25⇒÷４の手順で加工しています。
平方の差があらわれるので…

（ａ－ｂ）/（ａ＋ｂ）≧１/４となるパターンを精査すれば10通りになります。

大問６（空間図形）

（ア）　52.2％

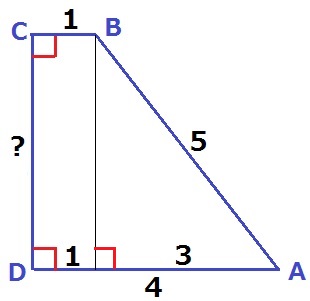
Ｂから垂線をひくと、３：４：５の直角三角形が見つかる。
ＣＤ＝４ｃｍ
台形ＡＢＣＤの面積は、（１＋４）×４÷２＝10ｃｍ²
四角柱の体積は、10×１＝10ｃｍ³　【２】

（イ）　42.6％

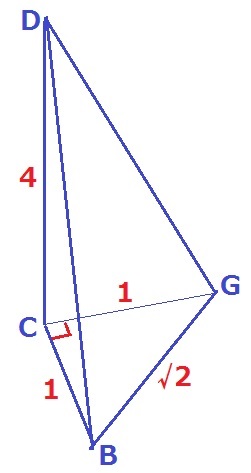
三角錐Ｄ―ＢＣＧの面ＢＤＧの面積を求める。
△ＢＣＧは直角二等辺で、辺の比は１：１：√２→ＢＧ＝√２ｃｍ

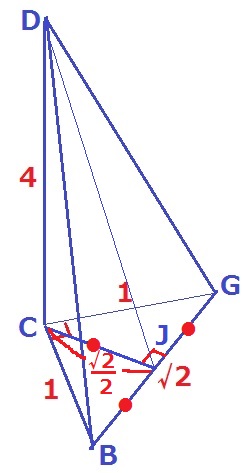
ＣからＢＧに向けて垂線、足をＪとするとＪはＢＧの中点。
ＣＪ＝√２÷２＝√２/２ｃｍ
△ＤＪＣで三平方→ＤＪ＝√（33/２）ｃｍ

△ＢＤＧは二等辺三角形で高さはＤＪにあたるから、
√２×√（33/２）÷２＝√33/２ｃｍ²　【４】

（ウ）　2.7％!!

最短距離なので展開図を作成。
ＩＤ＝４×③/⑩＝６/５ｃｍ
右側の斜めをどう処理すべきか。。

類題が2019年大問６でも出題されている（正答率1.7％!）。
最終的にＩＡを斜辺とする直角三角形の長さがわかればいい。
（ア）で３：４：５の直角三角形があったのでこれを活用する。
Ｆから垂線、足をＫとする。
△ＦＥＫと角を共有する直角三角形を右側に作成。
●＋×＝90°で角度を調査。
内角が×―●―90°の直角三角形は辺の比が３：４：５である。

△ＡＬＥでＡＥ＝１ｃｍだから、ＡＬ＝３/５ｃｍ、ＥＬ＝４/５ｃｍ

直角三角形ＩＡＭを作成。
ＩＭ＝６/５－３/５＝３/５ｃｍ
ＭＡ＝ＤＬ＝１＋４＋４/５＝29/５ｃｍ

最後に△ＩＭＡで三平方だが、最後も処理が重い。。
ＩＡ＝√｛（29/５）²＋（３/５）²｝
＝√｛（841＋９）/25｝
＝√（850/25）＝√34ｃｍ

大問１と大問２で配点が35点。
後半がアレなので失点は防ぎたい。
大問１
（ウ）通分するときは分子のカッコを忘れずに。
大問２
（エ）イスの問題って１脚あたり何人か座って座れない人が〇人でたとか、
△脚余ったという設定が多いが、単に並べるだけという。。
（オ）対称式は高１で習うが、埼玉の学校選択問題でも出てきた。
大問３
例年、変なのが紛れているので、ちょっと考えて無理そうなら後回し。
（ア）ⅱもう１組の対辺を平行にさせる→錯角か同位角を等しくさせる。
（イ）ちんけで不毛で瑣末な生産性のない作業を強いられることが、
いかに哀れで空虚で寂寥感のある物悲しい時間か、受験生をいたずらに混乱させるだけである????
せめて、選択肢の各ヒストグラムには下に中央値を与えておくべきだった。
神奈川の教育関係者はどう思ってるのか？？
（ウ）出しやすそうでなかなか手が届きにくい。
最初は試行錯誤してみるしかない。
（エ）取っ掛かりが見つけにくい。
与えられた３つの長さのうち、２辺が判明した△ＡＤＥと相似にあたる図形をどこかで作る。
大問４
（ウ）後半の大問では取りやすい。
解説ではＧの座標を特定し、△ＢＧＦから時計回りに面積比を算出した。
大問５
（イ）ひねくれてる人が問題作ったのかなって思った。
大問６
（イ）体積÷高さ＝底面積という手法もあるが、高さはＣとＢＧの中点ではない。
三平方を使ってチクチク求めていく。
（ウ）いくつかの小問をスルーしても大変。
幸い、過去問に類題があったが、作図も要するので短時間では厳しい。
（ア）の３：４：５の直角三角形を活用する発想を得たい。

＠2022年度・神奈川解説＠
数学(追検査)　社会…平均62.4点　理科…平均58.9点　英語…平均52.1点
公立高校入試解説ページに戻る

◆menu◆ 公立高校入試…関東圏メイン。千葉だけ５教科あります。％は正答率。
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→