平均53.0点(前年比;+0.1点)
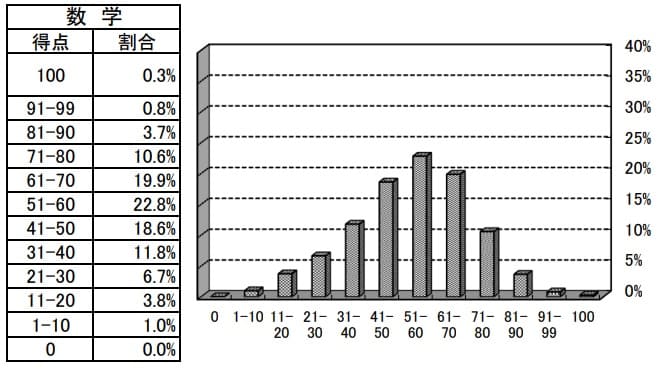
問題PDF
大問1(計算)
(ア) 94.7%
-1-(-7)
=-1+7
=6 【3】
(イ) 95.2%
-3/7+1/2
=1/14 【3】
(ウ) 85.8%
12ab2×6a÷(-3b)
=-24a2b 【1】
(エ) 91.4%
(3x+2y)/7-(2x-y)/5
={5(3x+2y)-7(2x-y)}/35
=(15x+10y-14x+7y)/35
=(x+17y)/35 【4】
(オ) 91.5%
(√6+5)2-5(√6+5) ←共通因数(√6+5)
=(√6+5)(√6+5-5)
=√6(√6+5)
=6+5√6 【2】
大問2(小問集合)
(ア) 92.1%
(x-5)(x+3)-2x+10 ←後半を2でくくる
=(x-5)(x+3)-2(x-5) ←共通因数(x-5)
=(x-5)(x+3-2)
=(x-5)(x+1) 【2】
(イ) 83.5%
7x2+2x-1=0
解の公式を適用。xの偶数だからb=2b’を用いて、
x=(-1±2√2)/7 【1】
(ウ) 81.9%
y=ax2において、xの値がp→qに増加したときの変化の割合はa(p+q)
-2{(-3)+(-1)}=8 【4】
(エ) 63.8%
もとの数の百の位をx、一の位をyとする。
入れ替えると396大きくなるので、x<y
(入れ替えた後)-(入れ替える前)=396
(100y+40+x)-(100x+40+y)
=99y-99x
=99(y-x)=396
y-x=4 …①
y+x=10 …②
①と②の連立を解いて、もとの数の一の位y=7 【2】
(オ) 78.0%
3780を素因数分解すると、3780=22×33×5×7
平方数にするには、すべての素因数を偶数個にする。
割算で3と5と7の素因数を1個ずつ取り除くと、残りは22×32=62になる。
n=3×5×7=105 【3】
大問3(小問集合2)
(ア)ⅰ ab…67.7%、c…89.0%
△AIF∽△EHGの証明。
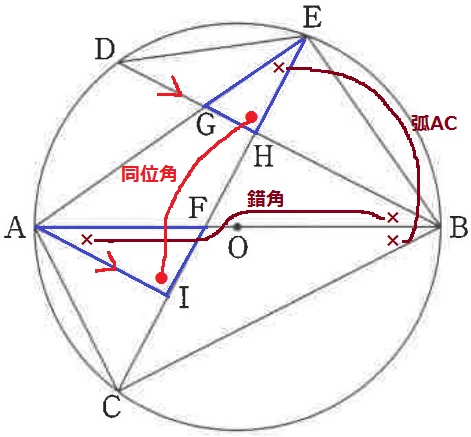
DB//AIの同位角で、∠AIF=∠EHG(●)
仮定より、∠ABC=∠ABD(×)
弧ACの円周角と錯角から、∠FAI=∠GEH(×)
2角が等しいので∽。
ⅱ 21.5%!
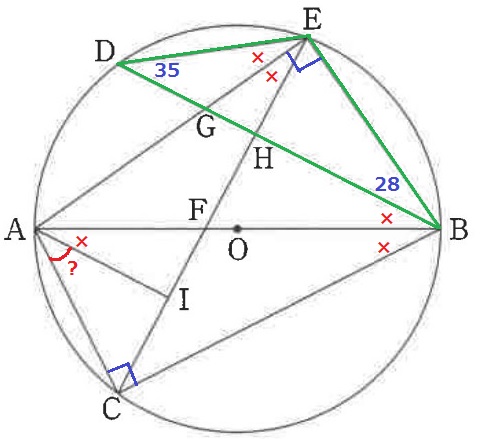
△ACIは前問の相似が使えない…。
そこで、等角の多かった×に注目してみる。
半円の弧に対する円周角は直角→∠AEB=∠ACB=90°
△ACBの内角から×がわかれば∠CAIが求まる。
弧ADの円周角より、∠AED=∠ABD=×
△EDBの内角から、∠GED(×)=180-(90+35+28)=27°
△ABCの内角から、∠CAI=180-(90+27×2)=36°
(イ)ⅰ 71.6%
資料1の値を昇順に並び替える。
【13、14、17、17、17、19、21、23、24、25】
最小値…13人
最大値…25人
第2四分位数(中央値)は5番目と6番目の平均…18人
第1四分位数は下位5つの真ん中(下から3番目)…17人
第3四分位数は上位5つの上から3番目…23人
これに適する箱ひげ図は【2】
ⅱ 44.2%
ここもYの10個を昇順に並べておく。
【15、19、20、20、20、24、24、25、26、27】
A:最頻値(モード)は最もあらわれている値。3クラスいる20人。〇
B:足しても良いが、個数が10クラスで同じだから平均を比較して、
【15、19、20、20、20(Z平均23)24、24、25、26、27】
平均下⇒-8-4-3-3-3=-21
平均上⇒+1+1+2+3+4=+11
Yの方が平均低い→Zの方が多い×
(*賛成者を計算するとY220人、Z230人になる)
C:Yの中央値(メジアン)は5番目と6番目の平均をとって22人。Yの方が大きい。〇
D:Yの第3四分位数は25人、第1四分位数は20人。
四分位範囲=第3四分位数-第1四分位数=25-20=5、Yの方が小さい。〇
【6】
(ウ) 27.8%!
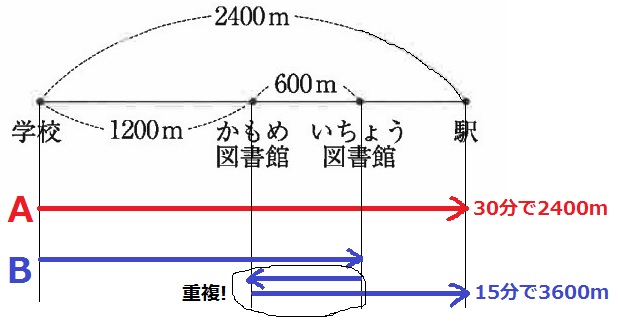
まずは両者のルートをおさえる。
図書館での滞在時間を除外すると、Aは30分で2400mを移動する。
Aの速さは、2400÷30=分速80m
Bの移動時間は、35-(15+5)=15分
2つの図書館を1往復余分に走っているので、移動距離は2400+600×2=3600m
Bの速さは、3600÷15=分速240m
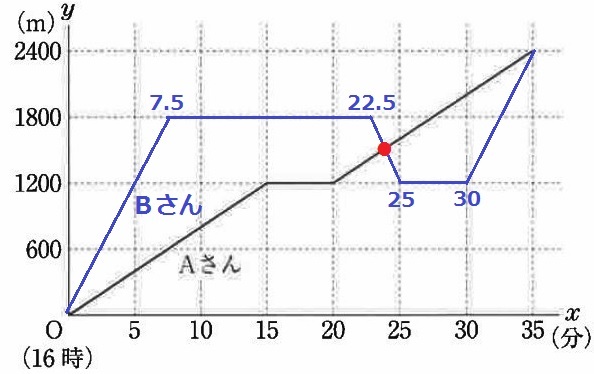
Bのダイヤグラムを描く。
いちょう図書館には、1800÷240=7.5分後に着く。
15分滞在して、かもめ図書館に移動。
距離が1/3だから、移動時間は7.5÷3=2.5分→25分後にかもめ図書館に到着。
5分滞在して、残りの5分で駅に着く。

22.5分後から30秒しかないので【3】だと思うが、一応確認しておく。
グラフの20~25分をピックアップ。
AとBの速さの比は、80:240=1:3
時間の比は逆比でA:B=③:①
赤線の距離をAは③、Bは①の時間で移動した。
④=5分だから、③=5×③/④=3分45秒
2人が出会った時刻は16時23分45秒。【3】
(エ) 8.0%!!
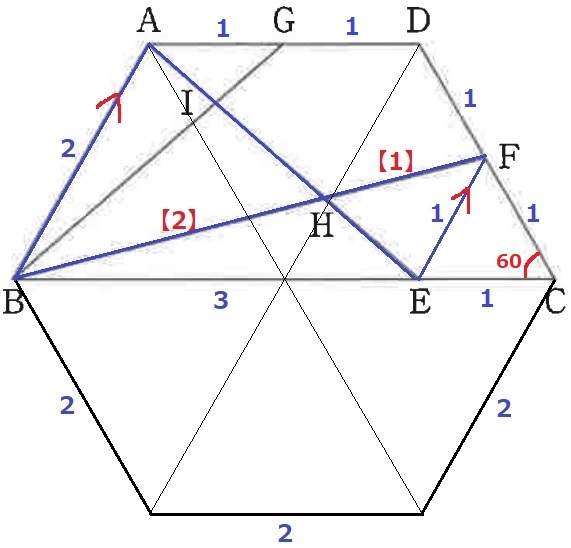
等脚台形ABCDをBCを対称の軸として下にもってくると、6辺が等しい正六角形があらわれる。
正六角形を6分割した正三角形の1辺は2。FC=EC=1、∠FCE=60°
→FEに補助線をひくと、△FECは正三角形。FE=1
AB//FE→△ABH∽△EFHから、BH:HF=2:1

△FECの面積を①とする。
BE:EC=3:1より、△FBE=③
BH:HF=2:1より、△HBE=②、△HEF=①
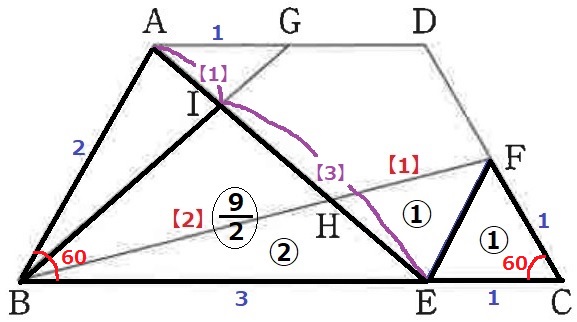
△ABEと△FECに着目する。同じ辺の比で∠ABE=∠FCEから隣辺比が使える。
隣辺比から、△ABE=2×3=⑥
△AIG∽△EIBから、AI:IE=1:3
△IBE=⑥×3/4=〇9/2
△BHI=〇9/2-②=〇5/2
S(△BHI):T(四角形CFHE)
=〇5/2:②
=5:4
大問4(関数)
(ア) 86.9%
y=-x+9にx=3を代入。
A(3、6)
これをy=ax2に代入して、
6=9a
a=2/3 【5】
(イ) 55.1%

Bはy軸についてAと対称→B(-3、6)
y=-1/6x2にx=-6を代入して、D(-6、-6)
Eはy軸についてDと対称→E(6、-6)
BDの傾きを求める。
Dから右に3、上に12移動するとBだから、傾きは12/3=4
Dから右に①、上に④移動してF
④=6なので、①=6×①/④=3/2
Fのx座標は、-6+3/2=-9/2
F(-9/2、0)
最後にEFの式を求める。連立使います。
-6=6m+n …①
-) 0=-9/2m+n …②
-6=21/2m
m=-4/7
①に代入、-6=6×(-4/7)+n
n=-18/7
ⅰ…【4】、ⅱ…【1】
(ウ) 5.9%!!

GはBCとDGの交点である。
y=-x+9にx=0を代入→C(9、0)
BCの式を出すと、y=-1/2x+9/2
DGの式が知りたい。
△BDGと△EDGが等積で、DE=12とキリが良い。

EDの延長線上にHD=12となるH(-18、-6)をおく。
HD=DEより、△HDG=△DEG
さらに△HDG=△BDGから等積変形よりHB//DGが成り立つ。
HからBは右に15、上に12で傾きは4/5。
y=4/5x+bに(x、y)=(-6、-6)を代入。
-6=4/5×(-6)+b
b=-6/5
DGの式は、y=4/5x-6/5
-1/2x+9/2=4/5x-6/5
13x=57
x=57/13
Gのx座標は57/13
大問5(確率)
(ア) 39.4%
ブロックが3ヵ所とも同じ個数→P・Q・Rに2個ずつ。

●1回目は4を出す。1~4をQに移動。2回目は2を出す。1~2をRに移動。
●1回目は2を出す。1~2をQに移動。2回目は4を出す。Pにある3~4をRに移動。
この2通りしかない。
全体は6×6=36通りだから、確率は2/36=1/18
@余談@
整数で整理するとわかりやすいかも。
【1、2│3、4│5、6】
1~6を並べて2個ずつに分ける。
仕切りはこの2ヶ所だから、(2、4)(4、2)しかない。
(イ) 34.5%
ブロックが0個になる場合はどういうときかを考える。
●同じ出目を2回出す
例えば(1、1)だと、1がP→Q→Rと流れてQが0個になる。
(6、6)では全部がP→Q→Rと流れてPとQが0個になる。
6通り
●1回だけ6を出す
1回目に6を出すとPがなくなる。2回目に1~5を出せば、Pだけが0個になる⇒5通り
逆の手順で1回目に1~5を出してQに移動し、2回目に6を出してPをゼロにする⇒5通り
6+5+5=16通り
確率は16/36=4/9
大問6(空間図形)
(ア) 62.5%
円錐の側面積=母線×半径×π
円錐の表面積は、4×4×π+10×4×π=56πcm2 【5】
(イ) 19.3%!
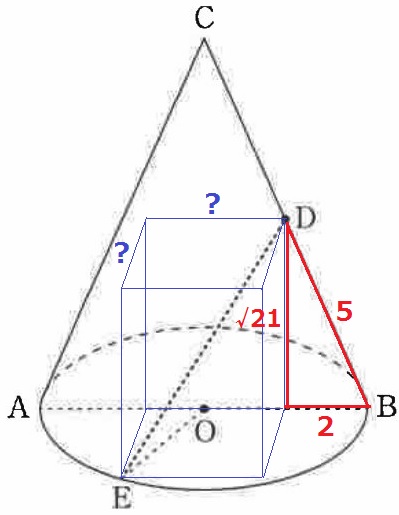
DEを対角線とする直方体を想像する。
1辺がa、b、cの直方体の対角線→√(a2+b2+c2)
Dの垂線の足はOBの中点を通る。
直方体の高さは赤線の三角形で三平方→√21cm
直方体の横と縦の長さを調べる。
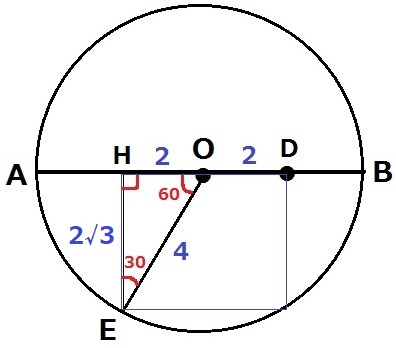
真上から見た図をつくる。
EからABに垂線をおろし、交点をHとする。
△HEOの内角は30°―60°―90°だから、辺の比は1:2:√3。
半径OE=4cm→HO=2cm、HE=2√3cm
直方体の高さは√21cm、横HD=4cm、縦HE=2√3cmなので、
DE=√{(√21)2+42+(2√3)2}
=√49=7cm 【2】
(ウ) 4.0%!!
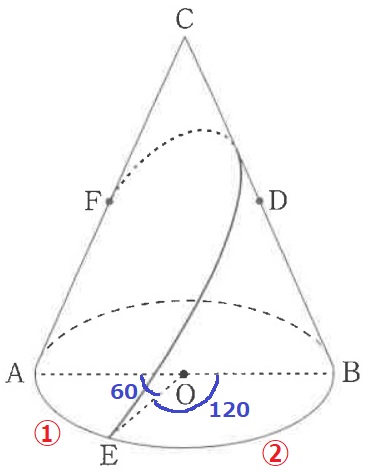
Eの位置を確認する。Eは弧AB上の点。
AE:EB=∠AOE:∠EOB=①:②
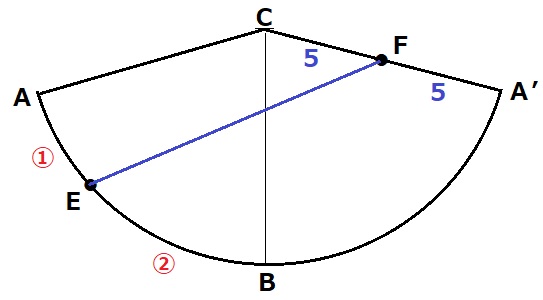
最短距離の問題は展開図を作成する。
Bは弧AA’の中点にある。
しかし、これだけではEFがわからない(;´・ω・)
他に使えそうな情報は中心角である。
円錐の側面積にあたる扇形の中心角は、〔360×半径/母線〕で求まる。
∠ACA’=360×4/10=144°
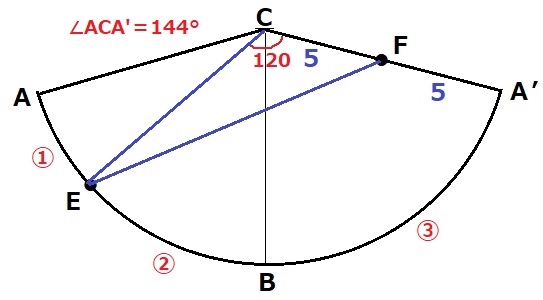
A’B=AB=③
中心角は弧の長さに比例するから、∠ECA’=144×⑤/⑥=120°!
有名角があらわれた。
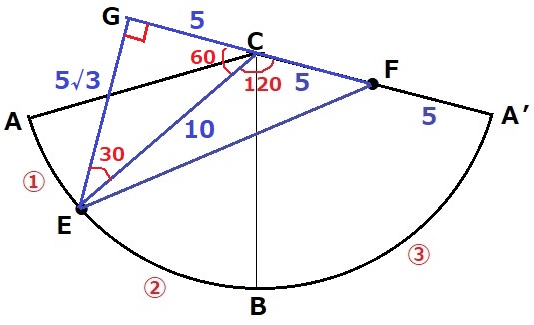
あとはおなじみのやり方。
A’Cを延長、Eから垂線をおろして足をGとする。
△ECGの内角から辺の比は1:2:√3。
GC=5cm、EG=5√3cm
最後に△EFGで三平方。
EF=√{(5√3)2+102}
=5√7cm
●講評●
大問1
15点とろう。
大問2
(ア)後半を2でくくると、共通因数(x-5)があらわれる。
(エ)十の位は同じ4で相殺。
差が400弱なので、百の位と一の位の差は4ではないかと想像できる。
(オ)割り算で素因数を消し、すべてを偶数個にする。
ここまで全問正解すれば35点。
大問3
(ア)ⅱ高得点を目指すには、なるべく時間をかけたくない。
前問の等角を頼りに調べていく。直径ABにも留意する。
(イ)ⅱ他に時間のかかる問いがあるので、あらかじめ昇順に載せた方が良かったかと。
(ウ)面食らった生徒は多かったと思われる。
全体の流れからBの速さを求め、Bの行動をダイヤグラムに記す。
すると、いちょう図書館を出発した時刻が16時22分30秒。
選択肢の様子から推測が許される設問であった。
(エ)特徴のある図形ゆえ解き方はいろいろあると思う。
解説では正六角形の分割で正三角形→2:1の相似比&隣辺比を使った。
出だしに迷ったら、右上に外側延長で比の合成を使うのが良い。
AI:IH:HE=3:5:4、BH:HF=2:1が得られる。
大問4
(イ)神奈川では分数が絡む直線の式を素早くかつ正確に出せることが前提か。
(ウ)GはBCとDGの交点。BとCの座標からBCは出せる。
DGと平行な直線を等積変形でつくり、傾きとD座標からDGが求まる。
大問5
設定はユニークだが易化した。
視点をおさえて整理すれば計算で答えを出せる。
大問6
(イ)他県でも出題される形式。直方体をつくって縦・横・高さを調べる。
(ウ)144°をどう扱うか。Eは弧ABを1:2に内分する位置にある。
弧の長さと中心角の関係を想起すれば道は開かれる。



コメント