問題はコチラ→ＰＤＦファイル
出題範囲の除外は三平方の定理と標本調査。
2021年度・京都前期の解説はコチラから。

大問１（小問集合）

（１）
（－４）²－９÷（－３）
＝16＋３＝19

（２）
６ｘ²ｙ×２/９ｙ÷８ｘｙ²
＝１/６ｘ

（３）
１/√８×４√６－√27

＝－√３

（４）
（７ｘ－３ｙ）－（２ｘ＋５ｙ）
＝５ｘ－８ｙ
＝５×１/５－８×（－３/４）
＝１＋６＝７

（５）
（ｘ＋１）²＝72
ｘ＋１＝±６√２
ｘ＝－１±６√２

（６）
ｘ＝２のとき、ｙ＝－２
ｘ＝６のとき、ｙ＝－18
変化の割合＝（ｙの増加量）÷（ｘの増加量）
＝{－18－（－２）}÷（６－２）＝－４

＠別解＠
ｙ＝ａｘ²において、ｘの値がｐ→ｑまで増加するときの変化の割合はａ（ｐ＋ｑ）。
－１/２×（２＋６）＝－４

（７）
点対称。回転の中心はＯ。

対応する点をつなげる。

（８）
４枚の表裏の出方は、２⁴＝16通り
◆４枚すべてが表
１通りしかない。
◆３枚が表
４枚のうち１枚だけが裏→４通り

合計５通り。
確率は、５/16。

大問２（データの活用）

（１）
階級値×度数の合計を15で割る。
（10×４＋14×８＋18×３）÷15
＝206÷15＝13.73…≒13.7℃

（２）

不等式にでてくる●―○で情報整理。
●はその数値を含み、○は含まない。

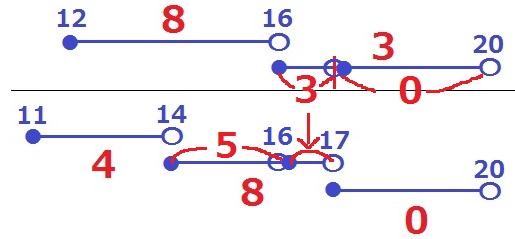
17℃以上20℃未満は０日。
16℃以上17℃未満は３日。
14℃以上16℃未満は、８－３＝５日

大問３（空間図形）

出題の仕方がすんごくシンプル( ;ﾟдﾟ)
（１）
錘の体積…底面積×高さ÷３
底面は１辺６ｃｍの正方形。
６×６×３√３÷３＝36√３ｃｍ³

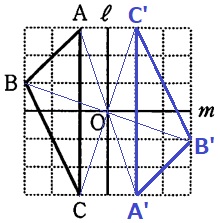
（２）

立面図の赤い正三角形を立体図で示すと右図のようになる。
底面積は１辺６ｃｍの正方形、側面積は底辺６ｃｍ、高さ６ｃｍの二等辺三角形。
表面積は、６×６＋６×６÷２×４＝108ｃｍ²

大問４（関数）

（１）
ｙ＝１/２ｘ＋２にｘ＝10を代入→Ｂ（10、７）
ｙ＝－ｘ＋５にｘ＝10を代入→Ｃ（10、－５）
ＢＣ間の距離は、７－（－５）＝12

＠＠
Ａはｙ＝１/２ｘ＋２とｙ＝－ｘ＋５の交点。
１/２ｘ＋２＝－ｘ＋５
ｘ＝２
ｙ＝－２＋５＝３
Ａ（２、３）
Ａのｘ座標とＢのｘ座標の差で距離を求める。
10－２＝８

（２）
（１）が本問の布石になっている。

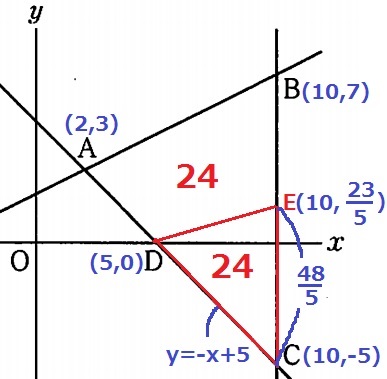
（Ｅの位置がおかしくて申し訳ない）
△ＡＢＣの面積は、12×８÷２＝48
ＤＥで△ＡＢＣを区切ると、△ＤＣＥの面積が24になればいい。
ｙ＝－ｘ＋５にｙ＝０を代入。Ｄ（５、０）
△ＤＣＥで底辺をＣＥとすると、高さはＤとＥＣの距離である５。
ＥＣ＝24×２÷５＝48/５
Ｅのｙ座標…－５＋48/５＝23/５

Ｄ（５、０）→Ｅ（10、23/５）
右に５、上に23/５移動するので、変化の割合は23/５÷５＝23/25
ｙ＝23/25ｘ＋ｂにＤ座標を代入。
０＝23/25×５＋ｂ
ｂ＝－23/５
ｙ＝23/25ｘ－23/５

大問５（平面図形）

（１）
Ａ，Ｂ，Ｃは円を３等分する点なので、
∠ＡＯＢ＝360÷３＝120°

（２）
円の３分の１である扇形ＯＡＢの面積が54πｃｍ²
円Ｏの面積は、54π×３＝162πｃｍ²
円の半径をｒとすると、πｒ²＝162πなので、
ｒ²＝162
ｒ＝√162＝９√２ｃｍ

（３）

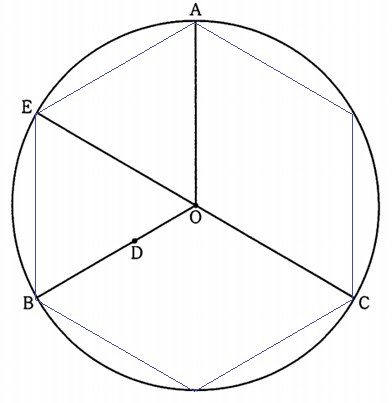
本問の図形を見たとき、サボは正六角形を思い浮かべました。
Ａ、Ｂ、Ｃが円周の３分の１、Ｅは弧ＡＢの中点。
△ＡＥＯと△ＥＢＯの内角はすべて60°で正三角形。
∠ＡＥＯ＝∠ＥＯＢで錯角が等しく、ＡＥ//ＢＯ。

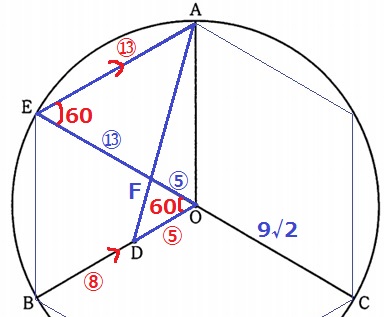
ＤＯ＝⑤、ＡＥ＝⑬
２角が等しく、△ＡＥＦ∽△ＤＯＦ。
ＥＦ：ＦＯ＝⑬：⑤
半径９√２ｃｍが⑱に相当する。
ＦＣ＝９√２×⑤/⑱＋９√２
＝23√２/２ｃｍ

大問６（規則）

（１）

魔方陣の要領で考えていく。
５番目のＡは、５×４＝20枚

（２）

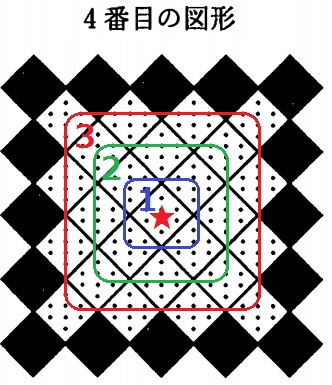
タイルＡだったところがタイルＢに変わっていく。
９番目のタイルＢの枚数は、１～８番目でタイルＡであった枚数の合計＋１。
最後の＋１は最初からタイルＢであった図形中央のタイルである。

Ａであった枚数の合計は、先ほどの魔方陣のやり方を応用して１～８番目を一括処理。
（１＋２＋３＋４＋５＋６＋７＋８）×４＋１
＝36×４＋１＝145枚

（３）
今までのおさらい。
ｎ番目のタイルＡ…４ｎ
ｎ番目のタイルＢ…（１～ｎ－１番目までの和）×４＋１。
１～ｎ－１までの和は、｛１＋（ｎ－１）｝×（ｎ－１）÷２＝１/２ｎ（ｎ－１）

４ｎ＋1009＝１/２ｎ（ｎ－１）×４＋１
２ｎ²－６ｎ－1008＝０
ｎ²－３ｎ－504
＝（ｎ－24）（ｎ＋21）＝０
ｎ＞０だから、ｎ＝24
答えは24番目の図形。