2021年度　三重県公立高校入試・前期過去問【数学】解説

問題はコチラ→ＰＤＦファイル
出題範囲の縮小は円周角と中心角、三平方の定理、標本調査。

大問１（小問集合）

（１）
４＋６×（－３）
＝４－18＝－14

（２）
１/３（２ｘ－５）－１/４（ｘ－７）
＝２/３ｘ－５/３－１/４ｘ＋７/４
＝（５ｘ＋１）/12

（３）
18ａ²ｂ÷６ａ×（－３ｂ）
＝－９ａｂ²←ここで代入
＝－９×（－５）×（２/３）²
＝20

（４）
４ｘ＋３ｙ＝１
３ｘ－２ｙ＝－12
加減法でがんばって解く。
ｘ＝－２、ｙ＝３

（５）
２√60－５/√15－√（５/３）
＝４√15－√15/３－√15/３
＝10√15/３

（６）
（ｘ＋３）（ｘ－３）＝２ｘ（ｘ－５）
ｘ²－９＝２ｘ²－10ｘ
ｘ²－10ｘ＋９
＝（ｘ－１）（ｘ－９）＝０
ｘ＝１、９

（７）
『ｙがｘの関数である』→ｘの値を決めると、それに応じてｙの値がただ１つに決まる関係。
ア：ｙ＝ｘ＋150　〇
イ：長方形の面積ｙは縦×横だが、周の長さｘから縦と横の長さはわからない×
（ｘ÷２で縦＋横の和はわかる）
ウ：体重と身長に関連性はない×
エ：ｘｙ＝45→ｙ＝45/ｘ 〇
ア・エ

（８）
側面積の扇形の中心角は〔×半径/母線〕で処理。
３×３×π＋５×５×π×３/５＝24πｃｍ²

（９）

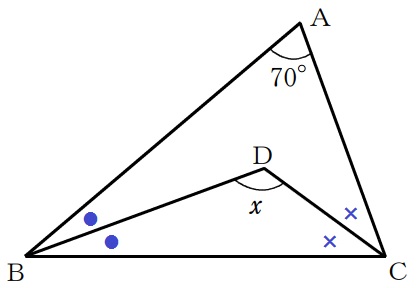
△ＡＢＣの内角で、●●＋××＝180－70＝110°
●＋×＝110÷２＝55°
△ＤＢＣの内角で、ｘ＝180－55＝125°

（10）

①接線と半径は接点で直交→Ｐを通るＡＢの垂線
②ＡＢとＢＣにも接する→円の中心はＡＢとＢＣから等距離→∠ＡＢＣの二等分線
③これらの交点が円の中心Ｏで、ＯＰを半径にぐるっと円を描く。

大問２（小問集合２）

（１）①
範囲（レンジ）＝最大値－最小値
19－１＝18冊

②
ア：平均値×個数＝総和。５×35＝175冊×
イ：35人の中央値（メジアン）は、（35＋１）÷２＝18番目の値。
　多い順に数えて18番目までは４冊以上借りている。〇
ウ：最頻値（モード）は３冊×
エ：最小値が１冊なので、全員１冊以上は借りている。〇
イ・エ

（２）①
（ａ、ｂ）＝（６、３）（５、４）（４、１）の３通り。
３/36＝１/12

②
ａｂの積が平方数になれば根号が外れる。
ａｂ＝１→（１、１）
ａｂ＝４→（１、４）（４、１）（２、２）
ａｂ＝９、16、25、36→（３、３）（４、４）（５、５）（６、６）
合計８通り。
８/36＝２/９

③
各頂点で止まる（Ｐ、Ｑ）の組合わせを調べる。
Ａで止まる→（４、４）
Ｂで止まる→（１、３）（５、３）
Ｃで止まる→（２、２）（２、６）（６、２）（６、６）
Ｄで止まる→（３、１）（３、５）
以上、９通り。
９/36＝１/４

大問３（空間図形＆規則）

（１）①

△ＢＦＧ∽△ＢＣＤから、△ＢＦＧ：四角形ＦＣＤＧの面積比がでる。
ＢＦ：ＦＣは△ＡＢＣ∽△ＥＦＣを利用する。
ＡＢ：ＥＦ＝ＢＣ：ＦＣ＝６：1.5＝④：①
ＢＦ：ＦＣ＝③：①
面積比は辺の比の２乗。
△ＢＦＧの面積…③×③＝【９】
△ＢＣＤの面積…④×④＝【16】
四角形ＦＣＤＧ…【16】－【９】＝【７】
△ＢＦＧ：四角形ＦＣＤＧ＝９：７

②
ＦＧ＝４ｃｍ
△ＢＦＣ∽△ＢＣＤで辺の比は３：４だから、
ＣＤ＝４×４/３＝16/３ｃｍ

（２）①

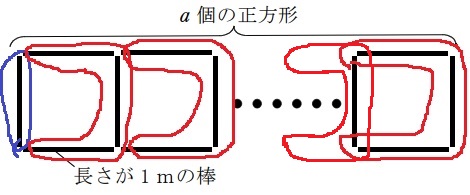
最初は１本だけ置いといて、ａ個分だけ３本の棒でコを増やす。
ア：１＋３×５＝16本
イ：３ａ＋１本

②
立体になった:;(∩´＿`∩);:

↑こんな感じで区切る。最初が４本で、８本ずつ追加。
ｂ＝（108－４）÷８＝13

大問４（数量変化）

（１）

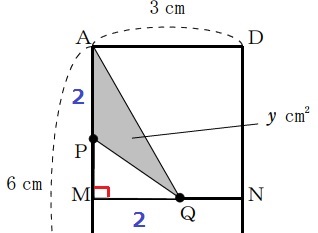
２秒後の様子。
△ＡＰＱの面積は、２×２÷２＝２ｃｍ²

（２）

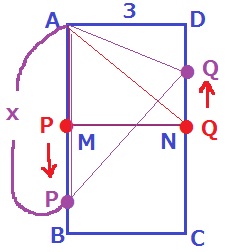
３～６秒後は、ＰはＭからＢ、ＱはＮからＤへ進む。
底辺ＡＰは伸びていくが、高さＡＤは３ｃｍで固定。
ｙ＝ｘ×３÷２＝３/２ｘ

（３）
面積が最大化となるのは、６秒後にＰがＢ、ＱがＤにいるとき。
（底辺ＡＰ＝ＡＢ＝６ｃｍで最長、高さＡＤは３ｃｍが最長）
６×３÷２＝９ｃｍ²

（４）
転換点に注意して調べる。
最初の変わり目は３秒後。
このとき、ＰはＭ、ＱはＮにいるので、△ＡＰＱの面積は３×３÷２＝4.5ｃｍ²
よって、４ｃｍ²は３秒前に起こる。

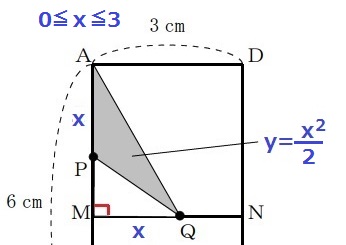
ｙ＝ｘ²/２
ｙ＝４を代入して、４＝ｘ²/２
ｘ²＝８
ｘ＞０ゆえｘ＝２√２

６秒後に面積が最大化。
そこから減少して９秒後にＰがＣ、ＱがＡに着いて０ｃｍ²になる。
先ほど４ｃｍ²となったのがスタートして３秒前だったから、
もう１個はゴール付近にあるはず。

ＡＱ＝４×２÷６＝４/３ｃｍ
秒速１ｃｍで、ゴールまで９ｃｍ動くから、
ｘ＝９－４/３＝23/３
ｘ＝２√２、23/３

（５）
まだ調べるのか！(´ﾟдﾟ｀)

△ＡＰＱが赤い三角形、△ＢＮＰが黒い三角形。
０≦ｘ＜３では赤＜黒の状態。赤増加、黒減少で、だんだん等しくなってくる。
ｘ＝３のときに面積が等しい！

等しくなってから３＜ｘ≦６では赤増加、黒減少。
６≦ｘ≦９で赤減少、黒増加で再び面積が近づいていく。
一番右の図に注目。
△ＡＰＱと△ＢＮＰの面積が等しいとき、高さの比が２：１だから底面の比は１：２。
ＡＱ＝①、ＢＰ＝②
ＰとＱは同じ速さだから、ＱＤ＝ＢＰ＝②
ＡＱ＝３×①/③＝１ｃｍ
秒速１ｃｍで全体で９ｃｍ動くので、９－１＝８秒後
ｘ＝３、８

大問５（平面図形）

（１）
△ＡＢＣ≡△ＧＡＤの証明。

仮定より、ＡＢ＝ＧＡ
平行四辺形の対辺で、ＢＣ＝ＡＤ
二等辺三角形ＡＢＧの底角⇒平行＋錯角で∠ＡＢＣ＝∠ＧＡＤ
以上、２辺のあいだの角が等しく合同。

（２）

ＡＨ＝③、ＨＤ＝②とおく。
平行四辺形の対辺でＢＣ＝⑤
△ＦＡＥ∽△ＣＢＥ。辺の比はＡＥ：ＢＥ＝１：１
ＦＡ＝ＣＢ＝⑤

△ＦＨＩ∽ＣＢＩに乗り換え。辺の比はＦＨ：ＣＢ＝⑧：⑤
ＢＩ：ＩＨ＝５：８

（３）

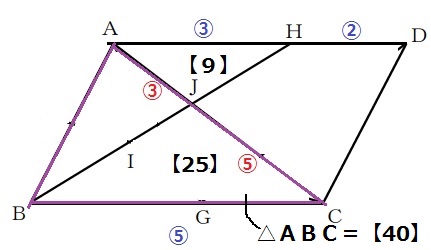
無駄な線を省くと、これだけで解けてしまう(；^ω^)
△ＡＪＨ∽△ＣＪＢで、辺の比は３：５。
△ＡＪＨの面積…③×③＝【９】
△ＣＪＢの面積…⑤×⑤＝【25】
ＡＣ：ＪＣ＝⑧：⑤だから、△ＡＢＣの面積…【25】×⑧/⑤＝【40】
△ＡＢＣは平行四辺形ＡＢＣＤの面積の半分なので、
△ＡＪＨ：平行四辺形ＡＢＣＤ＝９：80