2020年度　佐賀県公立高校入試過去問【数学】解説

平均25.2点（前年比；－1.6点）
問題はコチラ→ＰＤＦファイル

大問１（小問集合）－68％（6.8点）

（１）ア
６－17＝－11

イ
６÷（－２/３）
＝６×（－３/２）＝－９

ウ
２ｘ＋３ｙ－（ｘ＋５ｙ）/２
＝（４ｘ＋６ｙ－ｘ－５ｙ）/２
＝（３ｘ＋ｙ）/２

エ
（√３＋１）（√３－３）
＝（√３）²－２√３－３
＝－２√３

（２）
ｘ²＋９ｘ－36
＝（ｘ＋12）（ｘ－３）

（３）
単位換算に気を付けよう！ｂだけ単位がｃｍ。
ｍに統一。ｂｃｍ➡ｂ/100ｍ
ａ－ｂ/100＜２

（４）
球の体積…４/３πｒ³
球の半径は４÷２＝２ｃｍ
４/３π×２³＝32/３πｃｍ³

（５）
ｘ²＋３ｘ－１＝０
因数分解ができないので解の公式。
ｘ＝（－３±√13）/２

（６）

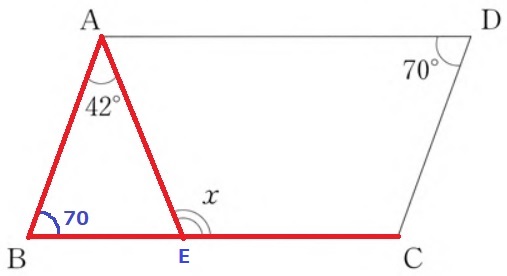
平行四辺形の対角は等しい→∠ＡＢＣ＝70°
△ＡＢＥで外角定理→ｘ＝42＋70＝112°

（７）
①10人の中央値（メジアン）は５番目と６番目の平均値。
Ａグループ…70点、Ｂグループ…50点で〇
②最頻値（モード）は最も表れている値。Ａグループ…70点、Ｂグループ…50点で×
③Ａグループ…２/10＝0.2、Ｂグループ…３/10＝0.3で×
④Ａグループ…７人、Ｂグループ…４人で〇
①、④

大問２（方程式・数量変化）－44％（4.4点）

（１）ア
１つは、割引されない運賃の合計。
15ｘ＋２ｙ＝9100…①
もう１つは、割引された運賃の合計。
４割引き→６割（0.6倍）
15ｘ×0.6＋２ｙ＝6100…②

イ
上の連立を解く。
15ｘ＋２ｙ＝9100
－)９ｘ＋２ｙ＝6100
６ｘ　　　＝3000
ｘ＝500
割引前の児童１人が500円。
これを４割引きして、500×0.6＝300円

（２）ア
◆２秒後
２×４÷２＝４ｃｍ²
◆４秒後
ＱはＢＣ上にくる。底辺４ｃｍ、高さはＡＢで６ｃｍ。
４×６÷２＝12ｃｍ²

イ

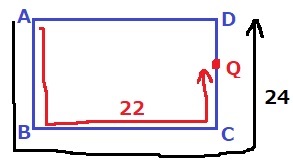
Ｑが進む長さは、２×11秒＝22ｃｍ
Ａ→Ｂ→Ｃ→Ｄまでの長さは、６＋12＋６＝24ｃｍ
ＤＱの長さは、24－22＝２ｃｍ

ウ（ａ）
前問と同じ考え。
スタート～ゴール（Ａ→Ｂ→Ｃ→Ｄ）までは24ｃｍで、
Ｑが進む距離は２ｘｃｍ。
ＤＱの長さは、24－２ｘｃｍ

（ｂ）
答案では過程も記述する。

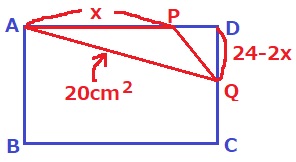
ｘ×（24－２ｘ）×１/２＝20　←カッコを展開、両辺を２倍
24ｘ－２ｘ²＝40
２ｘ²－24ｘ＋40＝０　←÷２
ｘ²－12ｘ＋20
＝（ｘ－２）（ｘ－10）＝０
Ｑは辺ＣＤ上だから９≦ｘ≦12（９～12秒後の範囲）
したがって、ｘ＝10
10秒後

大問３（確率・整数）－46％（4.6点）

（１）ア（ａ）
Ａは３通り、Ｂは３通りの出し方がある。
３×３＝９通り

（ｂ）
引き分けは（Ａ、Ｂ）＝（１、１）（２、２）（３、３）の３通り。
３/９＝１/３

（ｃ）
ＡとＢも手持ちのカードは同じ。
Ａの勝ちor負けの確率は等しい。
引き分けが１/３だから、Ａが勝つ確率は（１－１/３）÷２＝１/３

イ
３人の出し方は、３³＝27通り
Ａだけが勝つパターンを探す。
◆Ａが１
Ａは勝てない。
◆Ａが２
（Ｂ、Ｃ）＝（１、１）
◆Ａが３
（Ｂ、Ｃ）＝（１、１）（１、２）（２、１）（２、２）
計５通り
５/27

（２）ア
『百の位がａ、十の位がｂ、一の位がｃの数』を文字式で表す。
100×ａ＋10×ｂ＋ｃ
＝100ａ＋10ｂ＋ｃ

イ
300＋10ｂ＋６が８の倍数となるｂを求める。
８でくくれるところは８でくくる。
300＋10ｂ＋６
＝10ｂ＋306
＝８ｂ＋２ｂ＋304＋２
＝８（ｂ＋38）＋２ｂ＋２
②…ｂ、③…２ｂ＋２
*定数項部分は306÷８＝38…２

ウ
最後の２ｂ＋２が８の倍数であれば、300＋10ｂ＋６が全体で８の倍数になる。
ｂは十の位の数字なので、０≦ｂ≦９
ｂ＝３のとき、２ｂ＋２＝８
ｂ＝７のとき、２ｂ＋２＝16
ｂ＝３、７
④…３、⑤…７
*336÷８＝42、376÷８＝47

大問４（関数）－53％（5.3点）

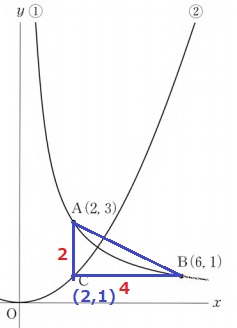
（１）
反比例はｘとｙの積が比例定数ａで一定。
ａ＝２×３＝６

（２）
ｙ＝１/４ｘ²にｘ＝２を代入。
ｙ＝１/４×２²＝１

（３）

座標を確認。２×４÷２＝４

（４）
Ａ（２、３）→Ｂ（６、１）
右に４、下に２だから傾きは－２/４＝－１/２
Ａから切片に向かう。左に２、上に１→（０、４）
ｙ＝－１/２ｘ＋４

（５）

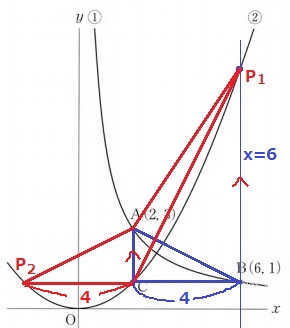
１つは等積変形でｘ＝６のとき。
ｙ＝１/４ｘ²に放り込む。
ｙ＝１/４×６²＝９
Ｐ₁（６、９）

もう１つはＡＣを底辺として負の方向にある。
ＢとＣのｘ座標の差が４。
ＣとＰ₂のｘ座標の差も４→Ｐ₂のｘ座標は２－４＝－２
ｙ＝１/４×（－２）²＝１
Ｐ²（－２、１）
（－２、１）（６、９）

（６）

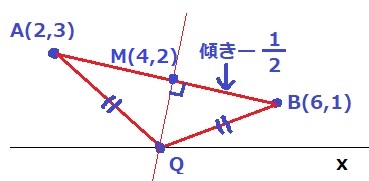
ＡＢの中点Ｍ（４、２）
ＱＭとＡＢは垂直に交わる。
【直交する２直線の傾きの積は－１】
ＡＢの傾きは（４）より－１/２。
ＱＭの傾きは、－１÷（－１/２）＝２
Ｍ（４、２）から左に１、下に２でＱ（３、０）

大問５（図形）－41％（4.1点）

（１）ア

辺の比が１：２の相似→３ｃｍ

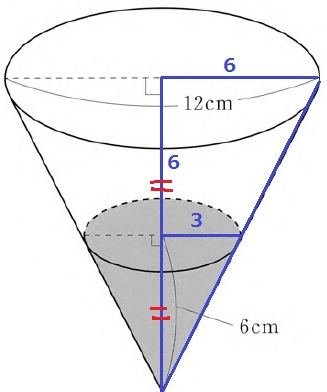
イ
体積比は辺の比の３乗。
２×２×２＝８倍

（２）ア
△ＡＢＦ≡△ＤＡＧの証明。

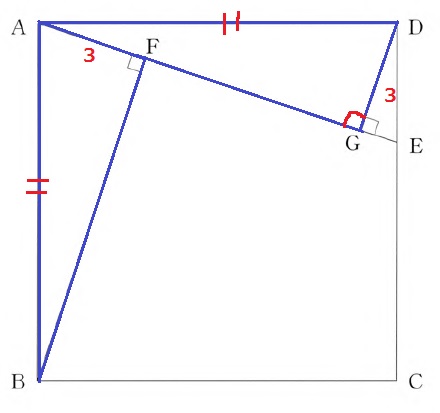
直角＋仮定の等辺＋正方形の１辺→斜辺と他の１辺が等しい直角三角形で合同。
*●＋×＝90°の角度を調査して、一辺両端角でも良い。

イ
△ＡＢＦで三平方→３√10ｃｍ

ウ

アの合同からＡＧ＝ＢＦ＝９ｃｍ
ＦＧ＝９－３＝６ｃｍ

△ＡＤＧと△ＤＥＧで、●＋×＝90°で調べると２角相等で∽。
ＡＧ：ＧＤ＝ＤＧ：ＧＥ＝３：１
ＧＥ＝１ｃｍ

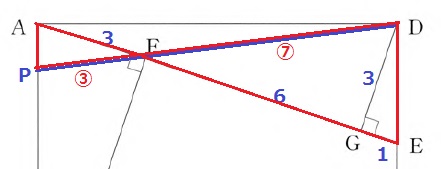
△ＡＦＰ∽△ＥＦＤより、辺の比からＰＦ：ＦＤ＝３：７
△ＡＦＰ：△ＡＤＦの面積比も３：７
△ＡＤＦは底辺ＡＦ＝３ｃｍ、高さＤＧ＝３ｃｍ
【△ＡＤＦ→△ＡＦＰ】
３×３×１/２×３/７＝27/14ｃｍ²

大問１
（３）ｂの単位に騙されないように！
（４）球の体積は思ったより正答率が良くない。公式は覚えておこう。
大問２
（２）イ全体の距離－Ｑの移動距離で求めたい長さがでる。
大問３
（２）イ出し方が面白かった。
８でくくれない部分が８の倍数になれば、全体で８の倍数となる。
大問４
前半は基本問題なので迅速に処理したい。
大問５
（１）空間は即答レベル。
（２）ウ最大の難所。ＰＦ：ＦＤを求めるには、どの三角形に注目すべきか。
△ＡＦＤはすぐ求められる点にも気がつきたい。
公立高校入試解説ページに戻る