問題ＰＤＦ
下の図のような、長方形ＰＱＲＳがあり、
２つの正六角形ＡＢＣＤＥＦＧＨ、ＧＨＩＪＫＬはともに面積が６ｃｍ2です。
点Ａ、Ｆ、Ｇ、Ｌは辺ＰＳ上の点で、点Ｃ，Ｄ、Ｉ、Ｊは辺ＱＲ上の点で、
点Ｂは辺ＰＱ上の点です。
正六角形ＧＨＩＪＫＬは、点Ｈと点Ｅが重なるとき、点Ｋは辺ＳＲ上にあります。
（１）
長方形ＰＱＲＳの面積は何ｃｍ2ですか。
（２）
２つの正六角形の重なる部分の面積が３ｃｍ2のとき、
ＰＦ：ＰＧを最も簡単な整数の比で表しなさい。
（３）
２つの正六角形の重なる部分の面積が１/２ｃｍ2のとき、
図形ＬＫＪＲＳの面積は何ｃｍ2ですか。
＠解説＠
（１）
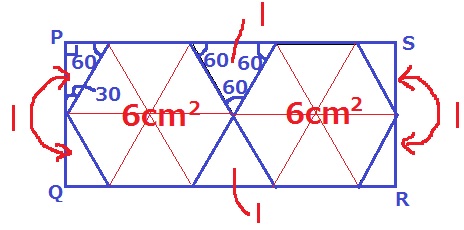
２つの正六角形が横に整列する。
正六角形は６つの正三角形に分割できる。
真ん中の上下２つの三角形は内角が60°で、１ｃｍ2の正三角形。
四隅は30°－60°－90°の直角三角形で、上下２つ合わせて正三角形となる。
16ｃｍ2
（２）
重なる部分（３ｃｍ2）を作図。
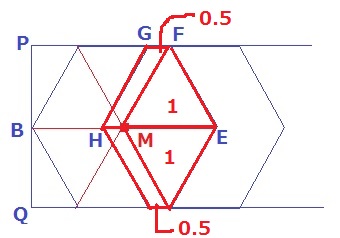
正六角形を６分割して重なり部分を捉える。
Ｆを通るＧＨに平行な線を描き、ＨＥとの交点をＭとする。
△ＦＭＥは１ｃｍ2の正三角形で、上下で２ｃｍ2。
残り１ｃｍ2は”くの字”の形となる。
くの字を分割した平行四辺形ＧＨＭＦの面積は0.5ｃｍ2。
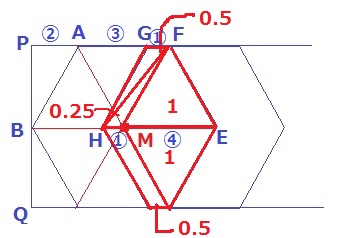
△ＦＨＭは0.25ｃｍ2。
ＨＭ：ＭＥ＝△ＦＨＭ：△ＦＭＥ＝0.25：１＝①：④
正三角形の１辺は④。平行四辺形の対辺でＧＦ＝ＨＭ＝①
ＡＧ＝④－①＝③
ＰＡ＝④÷２＝②
ＰＦ：ＰＧ＝６：５
（３）
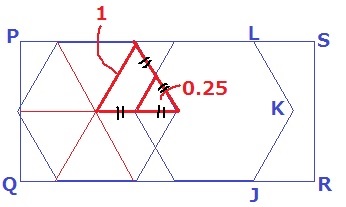
重なる0.5ｃｍ2は菱形になる。半分にして0.25ｃｍ2の正三角形。
ここでも正六角形を６分割した１ｃｍ2の正三角形で考える。
小さな正三角形と大きな正三角形の面積比は0.25：１＝１：４だから、辺の比は１：２
２つの正六角形は辺の中点で交わる。
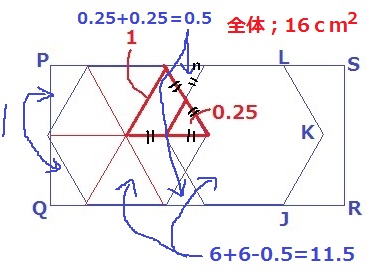
（１）より、長方形ＰＱＲＳは16ｃｍ2
２つの正六角形の合計は重複部分を引いて、６＋６－0.5＝11.5ｃｍ2
上下の隙間にある正三角形は0.25＋0.25＝0.5ｃｍ2
左の直角三角形は合わせて１ｃｍ2
図形ＬＫＪＲＳの面積は、16－（11.5＋0.5＋１）＝３ｃｍ2
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント