2020年度　千葉県公立高校入試過去問・後期【数学】解説

平均59.0点（前年比；－2.0点）

問題はコチラ→ＰＤＦファイル

大問１（計算）－89.2％

（１）　98.9％
６×（－３）
＝－18

（２）　92.1％
９－（－４）²×５/８
＝９－16×５/８
＝－１

（３）　90.1％
ａ²ｂ×21ｂ÷７ａ
＝３ａｂ²

（４）　88.4％
0.2ｘ＋1.5ｙ＝４　…①
ｘ－３ｙ＝－１　…②
①×10→２ｘ＋15ｙ＝40…③
③－②×２
２ｘ＋15ｙ＝40
－)２ｘ－６ｙ＝－２
21ｙ＝42
ｙ＝２
②に代入。ｘ－６＝－１
ｘ＝５
ｘ＝５、ｙ＝２

（５）　78.2％
12/√３－３√６×√８
＝４√３－３√48
＝４√３－12√３
＝－８√３

（６）　87.2％
ｘ²＋５ｘ＋５＝０
因数分解できないので解の公式。
ｘ＝（－５±√５）/２

大問２（小問集合）－53.8％

（１）　82.3％
不等式の意味を答える。
イコールを含まないので【2000円より高い】→イ

（２）　56.4％
最頻値（モード）は、最も度数が現われている値。
解答する際は階級値で答えること。
20と25の平均値→22.5ｍ

（３）　65.1％

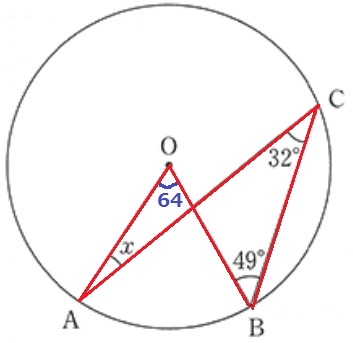
円周角定理より、∠ＡＯＢ＝32×２＝64°
赤線でチョウチョウ型。
チョウチョウの羽の２角の和は同じ。
64＋ｘ＝32＋49
ｘ＝17°

（４）　34.7％
６枚から２枚を選ぶ→₆Ｃ₂＝15通り
平均値が自然数になる組み合わせを拾い上げる。
（10、６）（10、－２）（６、－２）（３、－１）
この４通りしかない。
４/15

（５）６点－30.4％！　３点－5.0％　無答－26.8％
前期より方針は立てやすかった。
ＰはＯＢの中点なので、まずＢの位置を特定したい。
底面の円においてＢはＡの反対側。
すなわち、弧ＡＡ’の真ん中にＢがある。

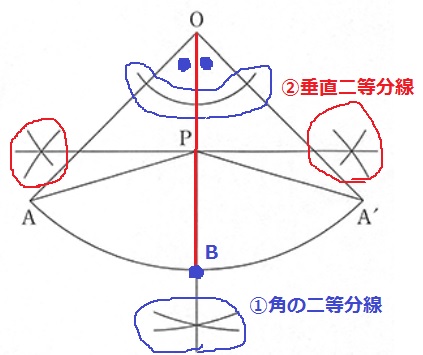
①∠ＡＯＡ’の二等分線。
②ＯＢの垂直等分線。
③ＡＰ、Ａ’Ｐを結べばＯＫ！

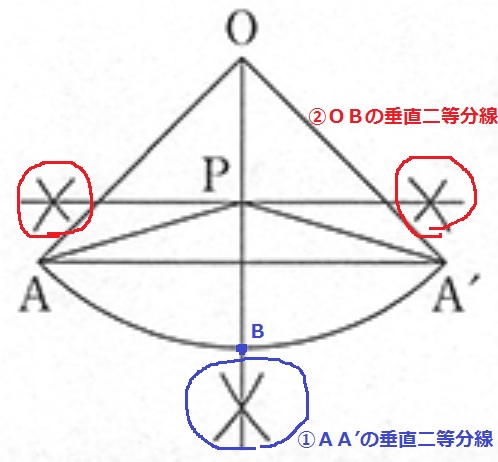
弦ＡＡ’を垂直に二等分してＢをだしてもＯＫ！
サボはこちらでやりました。

大問３（関数）－48.0％

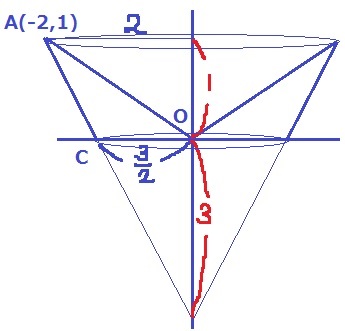
（１）　77.7％
ｙ＝－ｘ²より、Ｂ（３、－９）
『Ａのｙ座標はＢのｙ座標より10大きい』ので、
Ａのｙ座標は－９＋10＝１
Ａ（－２、１）をｙ＝ａｘ²に代入。
１＝４ａ
ａ＝１/４

（２）①　53.3％
Ａ（－２、１）→Ｂ（３、－９）
右に５、下に10なので、傾きは－10/５＝－２
Ａから右に２いくと下に４さがるから、
切片は１－４＝－３
ＡＢ；ｙ＝－２ｘ－３

ＣはＡＢとｘ軸との交点。
ｙ＝０を代入。
０＝－２ｘ－３
ｘ＝－３/２

②　12.9％！

ＡＢ；ｙ＝－２ｘ－３の切片から、下の高さは３ｃｍ。
逆さまのデカイ円錐から下にある逆さまの円錐を引き、
さらに、上にある平らな逆さまの三角錐をひけば出る。

体積比は辺の比の３乗を使ってももちろんできるが、
先に上のつぶれた円錐を取り除き、次に下の円錐を控除します。
２×２×π×４÷３×３/４－３/２×３/２×π×３÷３
＝４π－９/４π＝７/４πｃｍ³

＠別解＠
【回転体の体積＝面積×重心の移動距離】（←パップス＝ギュルダンの定理）

△ＡＣＯの面積…３/２×１÷２＝３/４ｃｍ²
△ＡＣＯの重心Ｇから回転の軸との半径ＧＨが知りたい。
ＡＤは中線で、ＤはＣＯの中点。
ＤＯ＝３/２÷２＝３/４ｃｍ
ＥＤ＝２－３/４＝５/４ｃｍ
△ＡＦＧ∽△ＡＥＤでＡＧ：ＡＤ＝２：３（重心は中線を２：１に内分）から、
ＦＧ＝５/４×２/３＝５/６ｃｍ
ＧＨ＝２－５/６＝７/６ｃｍ
よって、３/４×７/６×２×π＝７/４πｃｍ³

大問４（平面図形）－53.9％

（１）
まずは、△ＢＣＤ≡△ＡＣＥの証明から。

仮定から２組の辺が一緒なので、残りはあいだの角しかない。
∠ＢＣＡ＝∠ＤＣＥの各々から、あいだに挟まれる∠ＤＣＡをひけば、
∠ＢＣＤ＝∠ＡＣＥが導ける。合同条件は２辺とあいだの角。
ａ…ウ　91.1％
ｂ…オ　93.9％

ｃ…６点－23.3％！　３点－5.3％　無答－52.9％！
ＡＣが∠ＢＡＥの二等分線である証明。
先ほどの合同から、対応する角で∠ＥＡＣ＝∠ＤＢＣ
△ＡＢＣは二等辺だから、∠ＤＢＣ＝∠ＢＡＣ
以上より、∠ＢＡＣ＝∠ＥＡＣ→ＡＣは∠ＢＡＥの二等分線となる。
40分試験とはいえ平易。

（２）　7.3％!!
難所だが例年より正解率があがりそうな予感。
わざわざ角度の情報が与えられているということは、角度を調査せよということ。

△ＡＣＥと△ＢＣＤは合同なので、△ＢＣＤで考える。
ＡＣは∠ＢＡＥの二等分線だったので、∠ＢＡＣ＝50°
合同（もしくは二等辺）から∠ＡＢＣ＝50°、△ＡＢＣの残りで∠ＡＣＢ＝80°
∠ＤＣＢ＝80－20＝60°！

ＤからＢＣに垂線をひき、交点をＨとすると、
△ＤＣＨの内角は30°－60°－90°より、１：２：√３の直角三角形。
ＤＨ＝４×√３/２＝２√３ｃｍ
ＢＣ＝ＡＣ＝ａだから、△ＢＣＤ（△ＡＣＥ）の面積はａ×２√３÷２＝√３ａｃｍ²

大問５（数量変化）－32.3％

（１）　82.4％
ＰはＡＢ間を往復する。
図２より、20秒後にＢに着いて折り返す。
20秒後

（２）　28.1％！
四角形ＰＢＣＱの面積が最大となるには、ＰＢとＣＱの長さの合計が最長になればいい。
言い換えると、ＰＢ＝ＡＢかつＣＱ＝ＣＤのとき。
もっと言い換えると、ＰがＡにいてＱがＤにいるとき。
グラフ上でＡＰ＝０、ＣＱ＝Maxとなるのは40秒後。

（３）　40.3％
問題文から、ＢＥ＝ＤＥ＝24÷２＝12ｃｍ

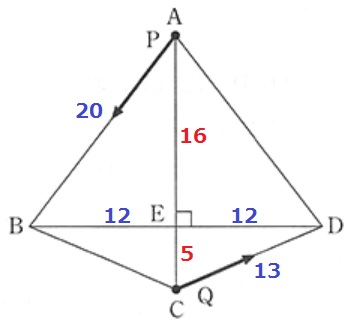
グラフよりＡＰ＝20ｃｍで折り返すということはＡＢ＝20ｃｍ
△ＡＢＥで三平方→３：４：５からＡＥ＝16ｃｍ
同様に、グラフよりＣＱ＝13ｃｍで折り返すのでＣＤ＝13ｃｍ
△ＣＤＥで三平方→５：12：13からＥＣ＝５ｃｍ
したがって、ＡＣ＝16＋５＝21ｃｍ

（４）①　10.3％！　無答－59.5％
０≦ｘ≦20は、ＰがＡを出発してＢに到着するまで。

△ＡＰＣにおいて、ＡＣを底辺とすると高さはＰＲにあたる。
ＰＲはｘに比例して長くなる。
Ｐが20秒後にＢへ着いたとき、ＰＲの長さは12ｃｍだから、
１秒あたりの変化の割合は12ｃｍ÷20秒＝３/５ｃｍ
ｘ秒後のＰＲの長さは３/５ｘｃｍとなる。
よって、Ｓ（△ＡＰＣの面積）＝21×３/５ｘ÷２＝63/10ｘ

②　0.2％!!!　無答－69.2％
△ＡＰＣと△ＡＱＣは、ともに底辺がＡＣで共通する。
ということは、高さが等しくなれば面積が等しい。

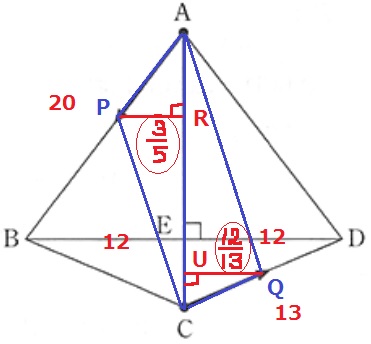
△ＡＱＣにおいて、先ほどのＰＲのように考えると、
ＱＵの変化の割合は１秒あたり12÷13＝12/13
１秒間でＰＲは３/５ｃｍ、ＱＵは12/13ｃｍずつ変化する。

14≦ｘ≦20は、ＱがＤに着いて折り返してから、ＰがＢに着くまで。
高さＰＲとＱＵの長さを縦軸において関係性をグラフであらわす。

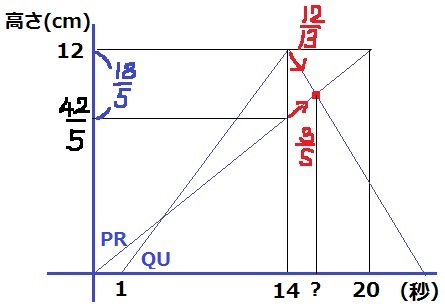
14秒後のＰＲは、３/５×14＝42/５ｃｍ
このとき、ＱＵとの高さの差は、12－42/５＝18/５ｃｍ
ここから１秒あたりＰＲは３/５ｃｍ長くなり、ＱＵは12/13ｃｍ短くなる。
１秒間で両者の差は、３/５＋12/13＝99/65ｃｍずつ近づいていく。
18/５ｃｍ÷99/65ｃｍ＝26/11秒
よって、２つの三角形の面積が等しくなるときは、14＋26/11＝180/11
ｘ＝180/11
*数量変化の問題は中学受験の解き方が染み込んでいるので、
高校受験界での王道な解法ではないかもしれません。

＠別解＠
こちらも先のダイヤグラムを使った、中学受験の戦法です。

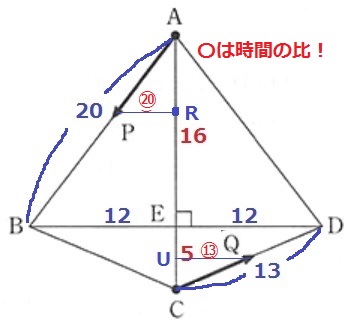
ＰＲが12ｃｍとなるのは20秒、ＱＵが12ｃｍとなるのは13秒かかる。
同じ長さになるまでの時間の比はＰＲ：ＱＵ＝⑳：⑬

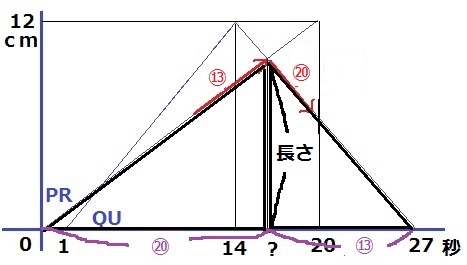
ＱＵは13秒で片道を渡るので、グラフの27秒後（＝１＋13＋13）に０ｃｍ。
左右の２つの三角形は高さが同じ。
三角形の高さは長さ。つまり、同じ長さだから先ほどの時間の比がそのまま当てはまる！
時間の比はＰＲ：ＱＵ＝⑳：⑬だから、？の値は、27×20/33＝180/11
これが最も処理手順の少ない解法かな？

＠2020年度千葉（前期）解説＠
数学…平均51.4点　社会…平均60.7点　理科…平均48.8点　英語…平均54.6点　国語…平均46.0点
＠2020年度千葉（後期）解説＠
社会…平均62.1点　理科…平均59.7点　英語…平均51.5点　国語…平均54.7点
その他の公立高校入試は下記の目次からどうぞです。
公立高校入試解説ページに戻る