2020年度　鳥取県公立高校入試問題過去問【数学】解説

平均25.7点（50点満点、前年比；－1.6点）

問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）①　95.1％
２－（－５）
＝２＋５＝７

②　94.0％
２/３÷（－２/15）
＝－５

③　90.8％
６√３－√27－√12
＝６√３－３√３－２√３
＝√３

④　87.0％
３（２ｘ－ｙ）－２（ｘ＋ｙ）
＝６ｘ－３ｙ－２ｘ－２ｙ
＝４ｘ－５ｙ

⑤　88.0％
３ａ²ｂ×４ａｂ²÷２ａｂ
＝６ａ²ｂ²

（２）　73.9％
（２ａ－３）²
＝４ａ²－12ａ＋９

（３）　73.4％
－ａ²－２ａ－１
＝－（ａ²＋２ａ＋１）
＝－（ａ＋１）²　←ここで代入
＝－（－２＋１）²
＝－（－１）²＝－１

（４）　83.7％
ｘ²－３ｘ－10
＝（ｘ＋２）（ｘ－５）

（５）式－68.5％、ア－77.2％
反比例はｘとｙの積が一定。
式；ｙ＝12/ｘ
ア；12÷２＝６

（６）　75.5％
ｘ²－３ｘ－１＝０
因数分解ができないので解の公式を適用。
ｘ＝（３±√13）/２

（７）　34.8％
側面積は半径６ｃｍの扇形。中心角は〔×半径/母線〕で対処しよう。
６×６×π×３/６＝18πｃｍ²

（８）　66.3％
48匹のうち、印付きは６匹。
印付きは全部で50匹だから、総数は48×50/６＝400匹

（９）　57.6％
３点を通る円の中心Ｏの作図。
ＡＢの垂直二等分線、ＢＣの垂直二等分線、ＣＡの垂直二等分線。
これら３本のうち２本を作図し、交点がＯとなる。

（10）　43.5％
△ＡＥＦ≡△ＤＥＣの証明。

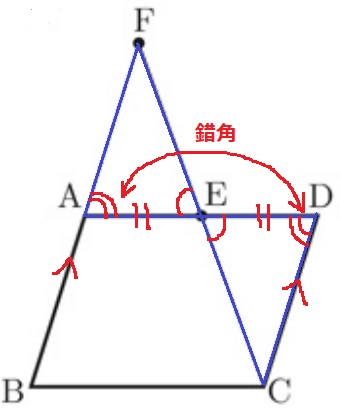
合同の証明では最低でも１組の等辺が必要なので、
ＡＥ＝ＤＥからどこの等角を指摘すべきかを捉える。
対頂角と平行線＋錯角で、１辺と両端角相等→合同。

（11）　56.0％
平均値はともに5.9点。
最頻値（モード）は最もあらわれている値。
10回の中央値（メジアン）は５番目と６番目の平均値。
そらの最頻値は７点、中央値は６点。
あずまの最頻値は９点、中央値は5.5点。
あずまを代表に選ぶので、最頻値を比較してあずまが大きい点を理由に挙げる。

大問２（確率）

（１）　58.7％
最も出にくい和は２。
（１、１）の１通りしかない。確率は１/36。
ア…２
イ…１/36

（２）　42.4％
６が最も出やすそうだが違うという。
〔１・２・２・３・３・３〕
〔１・２・２・３・３・３〕
和を６にするには３を２回出すので、３×３＝９通り
確率は９/36＝１/４

数字の並びをながめると、２＋３＝５の組み合わせが多そう。
和が５となる（２、３）は２×３＝６通り。
（３、２）も６通りだから、合計で12通りもある。
確率は12/36＝１/３
１/３＞１/４だから、出た目の数の和が５になる確率のほうが大きい。

（３）　21.7％！
ｙ＝ａｘ²に（ｍ、ｎ）を代入すると、
ｎ＝ａｍ²
ａ＝ｎ/ｍ²
ｎ/ｍ²の値が整数になる場合を考える。
〔１・２・２・３・３・３〕
分母ｍに２や３を入れてしまうとｎ/m²は整数にならない。
ｍ＝１で確定。
分母が１だから、分子ｎは何でも良い→６通り
６/36＝１/６

大問３（方程式）

（１）　58.7％
15分＝１/４時間
時速６ｋｍ×１/４時間＝３/２ｋｍ

（２）①82.1％、②81.0％
何をｘ、ｙに置いたかを問う。

よくあるパターン。
距離の合計が１周10ｋｍ。
道のり÷速さ＝時間で、時間の合計が６/５時間。

今度はｘ＋ｙ＝６/５となっているので、ｘとｙは時間。
１つ目は速さ×時間＝道のりで距離の等式を立てている。
①イ、②エ

（２）　38.6％
前問のどちらかの連立を解く。
１つ目の連立を解くとｘ＝３、ｙ＝７
走った距離は７ｋｍ。走った時間は７ｋｍ÷時速10ｋｍ＝７/10時間

２つ目の連立を解くとｘ＝１/２、ｙ＝７/10
走った時間は７/10時間。走った距離は時速10ｋｍ×７/10時間＝７ｋｍ
７ｋｍ、７/10時間

（３）①　13.0％！

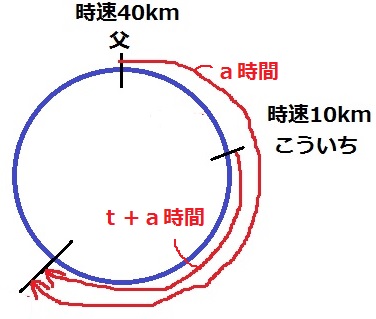
道のりの関係を表すので、〔速さ×時間〕を両辺に設置して道のりで等式を立てる。
こういちは父より先にｔ時間走っている点に注意！
父…時速40ｋｍ×ａ時間＝40ａｋｍ
こういち…時速10ｋｍ×（ｔ＋ａ）時間＝10（ｔ＋ａ）ｋｍ
10（ｔ＋ａ）＝40ａ

②　2.2％!!

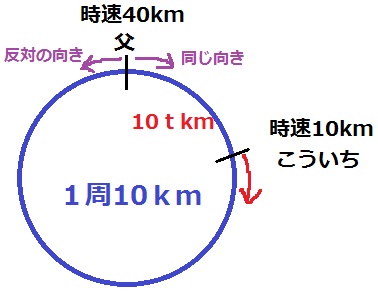
父が出発するｔ時間後は、２人の距離は10ｔｋｍ離れている。
ｔの値が小さければ２人の距離は接近しており、
父が反対の向きより同じ向きで出発して、こういちを追いかけた方が早く会える。
そのときのｔの最大値を求める。

父が反対の向きで出発すると、両者は時速50ｋｍで近づくので、
（10－10ｔ）ｋｍ÷時速50ｋｍ＝（10－10ｔ）/50＝（１－ｔ）/５時間で出会う。
父が同じ向きで出発すると、両者は時速30ｋｍで近づくので、
10ｔｋｍ÷時速30ｋｍ＝10ｔ/30＝１/３ｔ時間で追いつく。

（１－ｔ）/５＝１/３ｔ
３－３ｔ＝５ｔ
ｔ＝３/８
３/８時間後まで。

大問４（数量変化）

（１）　66.3％、51.1％
■プラン１
2500＋25×（220－100）
＝2500＋25×120＝2500＋25×４×30
＝2500＋3000＝5500円

■プラン２
1000＋20×（200－50）＋35×（220－200）
＝1000＋3000＋700＝4700円
プラン１…5500円　プラン２…4700円

（２）　32.1％！

50ｋＷｈまでは基本料金の1000円。
50～200ｋＷｈまでは傾きが20円。50ｋＷｈで1000円増加する。
200ｋｗｈ以降は傾きが35円。100ｋＷｈで3500円増加する。

（３）　26.1％！
先ほどのグラフにプラン１を書き込む。

プラン１は100ｋＷｈまで2500円、そこから傾き25円で上昇。
（200、5000）（300、7500）の格子点を通る。
300ｋＷｈでプラン１とプラン２の料金が7500円で等しくなるので、
300ｋＷｈ未満まではプラン２の方が安い。
300ｋＷｈ未満のとき

（４）　3.8％!!
（１）より、プラン２の料金は4700円。
プラン３の料金を考える。
基本料金は500円。
平日昼の電気使用量がａｋＷｈだから、平日昼分は35ａ円。
平日昼以外と土日祝日は１ｋＷｈあたり15円で同じ→まとめて処理！
２つの電気使用量は（220－ａ）ｋＷｈなので、料金は15（220－ａ）円。
これらの合計がプラン２の4700円より安い。
500＋35ａ＋15（220－ａ）＜4700
*ちなみに、この一次不等式を解くとａ＜45
平日昼の電気使用量を45ｋＷｈより小さく抑えればプラン３の方が安くなる。

大問５（図形）

（１）　63.6％

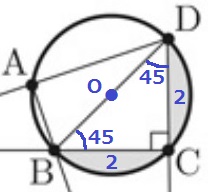
∠ＢＣＤ＝90°に着目する。
直径に対する円周角は90°
ＢＤが円の直径。
△ＢＣＤは直角二等辺三角形で辺の比は１：１：√２
ＢＤ＝２×√２＝２√２ｃｍ

（２）　35.3％

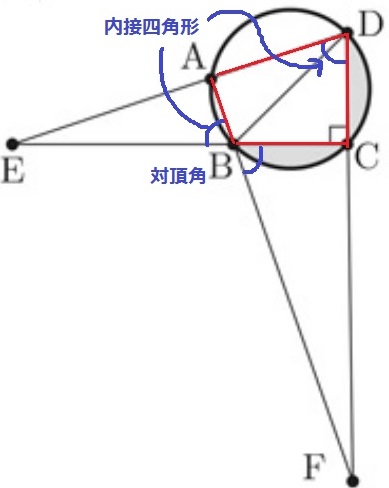
１つは対頂角で∠ＣＢＦ。
もう１つは内接四角形の内角は、その対角の外角に等しい→∠ＥＤＣ
ウ・オ

（３）　1.6％!!

結論からいうと、△ＡＢＥ∽△ＣＤＥ
前問の∠ＡＢＥ＝∠ＣＤＥ（●）。共通角∠ＡＥＢ＝∠ＣＥＤ（×）
２角相等で∽

△ＣＤＥでＤＣ：ＥＣ＝２：６＝①：③
辺の比で三平方→ＤＥ＝〇√10
△ＡＢＥでＡＢ：ＢＥ＝①：〇√10なので、
ＡＢ＝４×①/〇√10＝２√10/５ｃｍ

（４）　12.0％！

半径√２ｃｍの球のなかに、底辺の半径が√２ｃｍ、高さの合計が２√２ｃｍの円錐が入る。
斜線部分は〔球－円錐〕
４/３π×（√２）³－√２×√２×π×２√２÷３
＝８√２/３π－４√２/３π
＝４√２/３πｃｍ³

（５）　2.2％!!

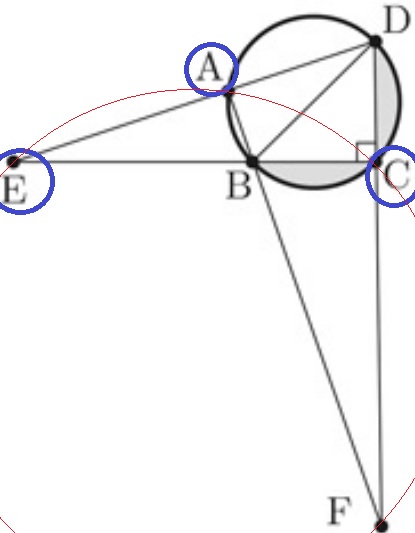
直径探し。どう見てもＥＣは直径ではない。
こういう場合は他の点も通るだろうと予測しよう。Ｆが怪しい。

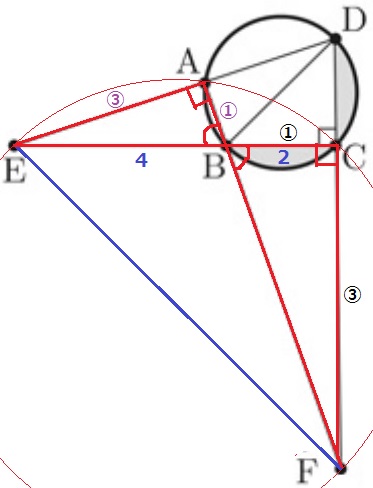
前問を手がかりに、∠ＥＡＦ＝∠ＥＣＦ＝90°
『２点Ａ、Ｃが直線ＥＦについて同じ側にあって、∠ＥＡＦ＝∠ＥＣＦが成り立つから、
４点Ａ、Ｅ、Ｆ，Ｃは同一円周上にある』（円周角定理の逆）
等角が90°なので、円Ｐの直径はＥＦとなる。

ＥＦは△ＣＥＦの三平方で求まるので、ＣＦが知りたい。
２角相等→△ＡＢＥ∽△ＣＢＦ
（３）の辺の比から、△ＡＢＥでＡＢ：ＡＥ＝①：③
ＣＢ：ＣＦ＝①：③ゆえ、ＣＦ＝２×３＝６ｃｍ
△ＣＥＦで三平方→１：１：√２の直角三角形からＣＦ＝６√２ｃｍ