2020年度　秋田県公立高校入試問題過去問【数学】解説

平均51.5点（前年比；－2.2点）

問題はコチラ→ＰＤＦファイル

大問１（小問集合）

〔15問の中から指示された８問を解く〕
（１）　70.9％
１＋（－0.2）×２
＝１－0.4＝0.6

（２）　87.6％
有理化。
６/√２　←分母分子に√２をかける
＝６√２/２
＝３√２

（３）　86.4％
３（ａ－２ｂ）－５（３ａ－ｂ）
＝３ａ－６ｂ－15ａ＋５ｂ
＝－12ａ－ｂ
＝－12×（１/２）－３
＝－９

（４）　62.6％
不等式。
３ａ+２ｂ≧30

（５）　79.1％
（２ｘ＋４）/３＝４　←両辺を３倍して左辺の分母を払う
２ｘ＋４＝12
２ｘ＝８
ｘ＝４

（６）　88.7％
２ｘ－３ｙ＝－５　…①
ｘ＝－５ｙ＋４　…②
②を①に代入。
２（－５ｙ＋４）－３ｙ＝－５
－13ｙ＝－13
ｙ＝１
②に代入。
ｘ＝－５×１＋４＝－１
ｘ＝－１、ｙ＝１

（７）　54.5％
『解の１つが－１』→ｘに－１を代入。
（－１）²－２×（－１）ａ＋３＝０
２ａ＝－４
ａ＝－２

次に、ａ＝－２を放り込む。
ｘ²＋４ｘ＋３
＝（ｘ＋１）（ｘ＋３）＝０
したがって、もう１つの解はｘ＝－３

（８）　9.3％!!
往復の速さ＝〔往復の距離〕÷〔往復の時間〕
往復の距離＝２ａ
往復の時間＝行きの時間＋帰りの時間
＝ａ/60＋ａ/90＝１/36ａ
往復の速さは、２ａ÷１/36ａ＝72

（９）　42.0％
Ｐ⇒Ｑ（ＰならばＱが成立する）の命題の逆はＱ⇒Ｐ（ＱならばＰが成立する）。
（ちなみに、裏はＰでない⇒Ｑでない、対偶はＱでない⇒Ｐでない）
Ｐ⇒Ｑが真であるとき、対偶は常に真であるが、逆と裏は必ずしも真ではない（偽）。
ただし、命題の中身によっては逆や裏も真となる場合がある。

アの逆：すべての内角が等しい三角形⇒正三角形
１つの内角は180÷３＝60°、これが３つなので正三角形といえる〇
イの逆：対角線がそれぞれの中点で交わる四角形⇒長方形
正方形を特別な長方形と捉えても、菱形や平行四辺形がある×
ウの逆：ｘ＞４⇒ｘ≧５
４＜ｘ＜５は当てはまらず×
エの逆：ｘ²＝１⇒ｘ＝１
ｘ＝－１がある×

（10）　8.3％!!
地道にあてはめていく戦法が使えない(;´Д｀)
整数になる→根号が外れる→根号の中が平方数
つまり、120＋ａ²の値が平方数になればいい。
この平方数をｂ²とする。
120＋ａ²＝ｂ²（ｂ²の方がａ²より値が大きいのでａ＜ｂ）
ｂ²－ａ²
＝（ｂ＋ａ）（ｂ－ａ）＝120
積が120となる（ｂ＋ａ）と（ｂ－ａ）の組み合わせをピックアップ。
120×１、60×２、40×３、30×４、24×５、20×６、15×８、12×10
120×１の場合、ｂ＋ａ＝120、ｂ－ａ＝１
和が偶数ということは偶数＋偶数か奇数＋奇数となるところ、いずれも差は偶数になる。
しかし、差の１が奇数なので、ａは自然数とならず不適。
同様に、120×１のように偶数と奇数のパターンは外れることになる。
残りは60×２、30×４、20×６、12×10の４通り。
偶数と偶数であれば和も差も偶数となるので、ａは自然数となる。
よって、ａは４個。
*試しに計算すると、
【60×２】
ｂ＋ａ＝60、ｂ－ａ＝２
ｂ＝31、ａ＝29
【30×４】
ｂ＝17、ａ＝13
【20×６】
ｂ＝13、ａ＝７
【12×10】
ｂ＝11、ａ＝１
ａ＝１、７、13、29の４個。

（11）　88.3％

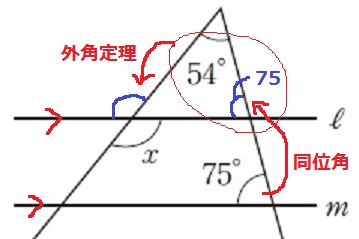
同位角で75°を上へ。
外角定理より、75＋54＝129°
対頂角でｘ＝129°

（12）　80.1％

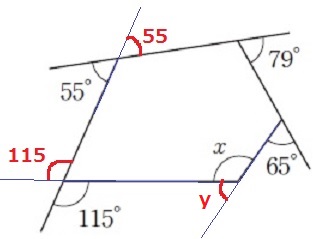
対頂角で移動すると、すべて外角の位置にくる。
多角形の外角の和は360°
ｙ＝360－（55＋115＋65＋79）
＝360－314＝46°
ｘ＝180－46＝134°

（13）　26.1％！
ＡＢとネジレの位置にある辺の本数を求める。
けっこうシビア(;´･ω･)

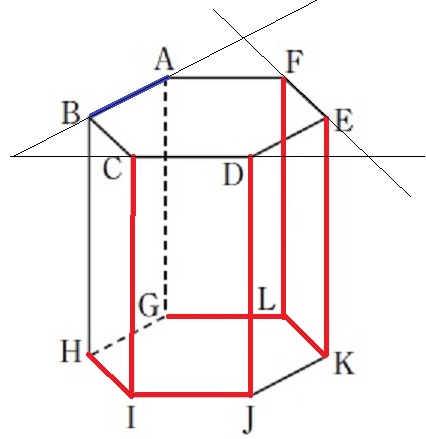
ネジレの位置→延長しても交わらない、かつ平行ではない。
ＣＤとＥＦは延長するとＡＢと交わる！
ネジレは赤線の８本。

（14）　48.9％
高さは三平方の定理で算出。
√（５²－２²）＝√21ｃｍ
２×２×π×√21÷３＝４√21/３ｃｍ³

（15）　29.0％！

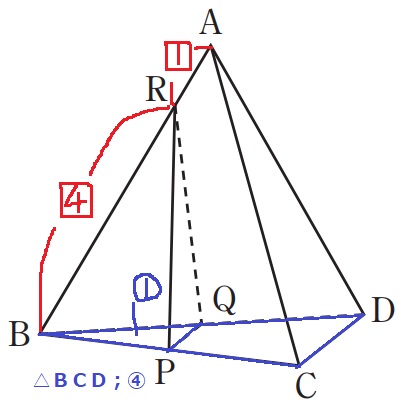
底辺の比→△ＢＰＱ：△ＢＣＤ＝①：④
高さの比→ＲＢ：ＡＢ＝□４：□５
体積比→Ｒ－ＢＰＱ：Ａ－ＢＣＤ
＝①×□４：④×□５＝１：５
５倍

大問２（小問集合２）

（１）　40.7％
ｙ＝３/ｘ→反比例
ｘが増えたらｙは減る。
これはａが正でも負でも同じことがいえる。
イ・エ

（２）①　70.2％
過程も記述する。
ｂはＱのｙ座標。先にグラフの式を求める。
ｙ＝ａｘ²にＰ（６、９）を代入。
９＝36ａ
ａ＝１/４

ｙ＝１/４ｘ²にｘ＝－２を代入。
ｙ＝１/４×（－２）²＝１
ｂ＝１

②　ｃ…39.2％、ｄ…31.4％！
ａ＜０なので、上に凸のグラフ。
グラフが原点を通過するかわからないので、
まずｙ＝－８のとき、ｘの値を考える。
－８＝－１/２ｘ²
ｘ＝±４
ｘ≦２であるから、ｘ＝－４
ｘ＝－４のとき、最小値ｙ＝－８
ｃ＝－４

ｘの変域が－４≦ｘ≦２ということは原点を通過する。
ｘ＝０のとき、最大値ｙ＝０
ｄ＝０

（３）　55.1％
Ｏを回転の中心としてＰを時計回りに45°回転させる。
①Ｏを通る直線ℓに垂直な線分を作図。
②90°の二等分線の作図。
③ＯＰの長さをとり、二等分線上に移してＱ。

（４）　9.0％!!

ＤＥ＝②、ＥＣ＝①とする。ＡＢ＝③
△ＡＢＦ∽△ＥＤＦから、ＢＦ：ＤＦ＝３：２
平行四辺形ＡＢＣＤ→△ＢＣＤ→△ＦＣＤ→△ＦＥＤ
１×１/２×２/５×２/３＝２/15倍

大問３（数量変化）

（１）①　95.0％
数量は4000ｍＬで強運転は４時間で空になるから、
4000÷４＝1000ｍＬ

②　74.2％

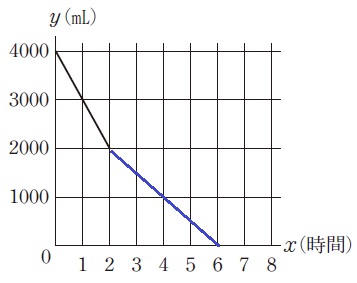
弱に切り替えて４時間で空になったから、６時間後に０となる。
計算は不要。

（２）①　41.1％
やり方が少し独特なので、グラフの説明からいきます。

左は4000ｍＬから始めた中運転。すると、５時間で終わってしまう。
真ん中は７時間で終了する予定の弱運転。はじめは4000ｍＬではない。
右は２つのグラフを重ねたもの。青→赤といけば中運転から弱運転に切り替えて７時間で終わる。
弱運転に切り替えた時間は、直線ＰＱと直線ＲＳの交点のｘ座標（ｂ）

②　ｃ…48.5％、ｄ…44.9％、ｅｆ…38.8％
ＰＱの式…変化の割合は－4000÷５＝－800
切片が4000なので、ｙ＝－800ｘ＋4000（ｃ）

ＲＳの式…（５、1000）→（７、０）から変化の割合は－1000÷（７－５）＝－500
０＝－500×７＋ｂ
ｂ＝3500
ｙ＝－500ｘ＋3500（ｄ）

２つの直線の交点座標を求める、
－800ｘ＋4000＝－500ｘ＋3500
300ｘ＝500
ｘ＝５/３時間＝１時間40分
１（ｅ）40（ｆ）

＠別解＠

本問は穴埋めなので、いやがおうでも方程式を経由しなければならないが、
答えを出すだけならば相似図形の方が圧倒的に早い。
左のグラフで、△ＳＲＱ∽△ＴＲＵから、ＴＵ＝1000×７/２＝3500
右のグラフで、△ＰＶＴ∽△ＱＶＳから、
ＰＶ：ＱＶ＝ＰＴ：ＱＳ＝500：1000＝１：２
Ｖのｘ座標は０～５時間を１：２に内分する。
５時間×１/３＝５/３時間＝１時間40分

大問４（データの活用・確率）

（１）　68.8％
最頻値（モード）…最もあらわれている値。
解答は階級値で答えること！
Ａのモードは14.2秒（ア）
Ｂのモードは14.4秒（イ）
速いのはＡ（ウ）

（２）①　53.9％
４の倍数なので、どちらかに４がでれば残りは何でもいい。
（１・４）（２・４）（３・４）（５・４）（６・４）の逆を含めて10通り
＋（４・４）＝11通り。
残りは４以外の偶数である２と６を使う。
（２・６）の２通り＋（２・２）（６・６）の２通り＝４通り
計15通りで、15/36＝５/12

②　26.0％！
素数なので１個ずつ試していくしかない…。
ａは十の位、ｂは一の位。
（ａ、ｂ）＝（１、１）（１、３）（２、３）（３、１）
（４、１）（４、３）（５、３）（６、１）の計８通り。
８/36＝２/９

大問５（平面図形）

〔次のⅠ・Ⅱから指示された問題を解く〕
Ⅰ（１）　58.0％

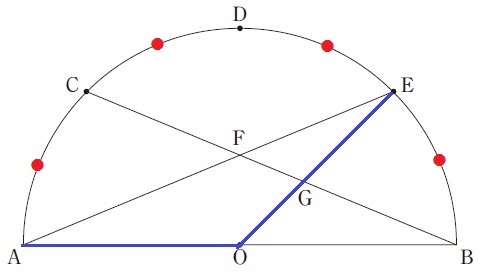
∠ＡＯＧを∠ＡＯＥで捉える。
中心角は弧の長さに比例するので、
∠ＡＯＧ＝180×３/４＝135°

（２）　15.7％！
△ＦＡＢが二等辺三角形であることの証明。

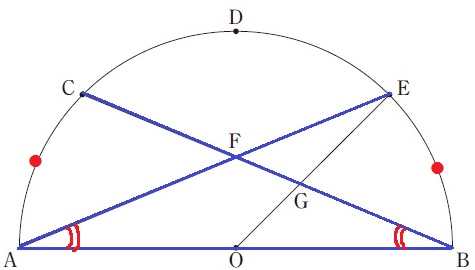
弧ＡＣ＝弧ＢＥ
等しい弧に対する円周角は等しいので∠ＡＢＣ＝∠ＢＡＦ
△ＦＡＢは２角が等しいから二等辺三角形。

（３）　4.1％!!

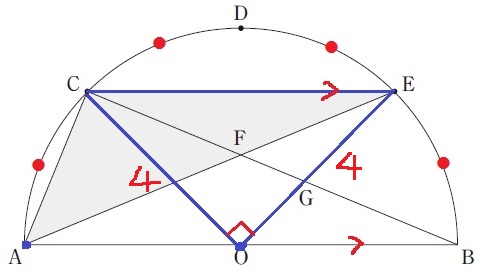
ＤはＯの真上にあり、ＣはＤＡ、ＥはＤＢの中点にある。
ＣとＥは直径ＡＢから同じ高さにある→ＣＥ//ＡＢ
等積変形で△ＡＣＥを△ＯＣＥに変える。
∠ＣＯＥ＝180×２/４＝90°
半径と合わせると、△ＯＣＥは直角二等辺三角形。
４×４÷２＝８ｃｍ²

Ⅱ（１）　31.5％！
△ＨＯＢが二等辺三角形であることの証明。

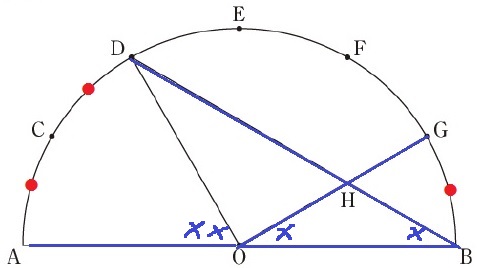
弧ＧＢの円周角である∠ＧＯＢ＝×とする。
中心角の大きさは弧の長さに比例するので、
弧ＡＤの中心角である∠ＤＯＡ＝××
その円周角∠ＤＢＡ＝×
△ＨＯＢは２角が等しくなり、二等辺三角形。

（２）　21.5％！

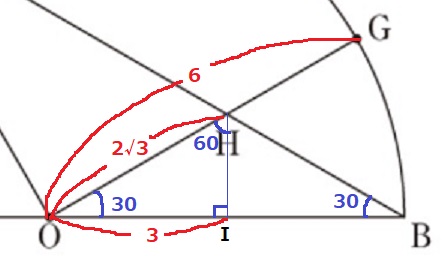
∠ＧＯＢ＝180÷６＝30°
二等辺三角形ＨＯＢの頂角Ｈから底辺に向けて垂線、その足をＩとすると、
△ＯＨＩの内角は30°－60°－90°の直角三角形。
ＯＨ＝３×２/√３＝２√３
ＧＨ＝６－２√３ｃｍ

（３）　10.8％！
形が複雑なので、形を変えられないか考える。
ポイントは白い部分を等積変形する。

ＥはＯの真上にあり。ＤとＦは直径ＡＢからの高さが等しい。
ＤＦ//ＡＢより、△ＡＤＦを△ＯＤＦに変形。
すると、白い部分が扇形ＯＤＦに変わる。

下の白は、扇形ＯＧＢとそれ以外に分け、
ＣＧ//ＡＢから△ＡＧＯを△ＡＣＯに変形する。

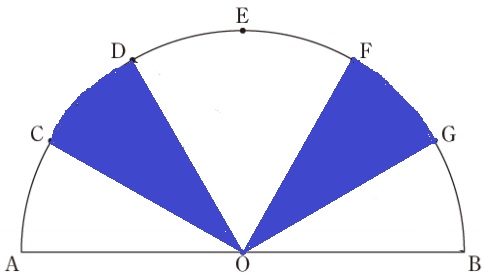
まとめると、白い部分がこのような形になる。
求積すべき範囲は青いところ。
６×６×π×１/２×２/６＝６πｃｍ²

＠余談＠

2017年度の東大寺学園中学に類題があったようです( ´д)ﾋｿ(´д｀)ﾋｿ(д｀ )
難しい問題ですが、小学生でも発想力を駆使してチャレンジできますね！