2023年度　青森県公立高校入試問題過去問【数学】解説

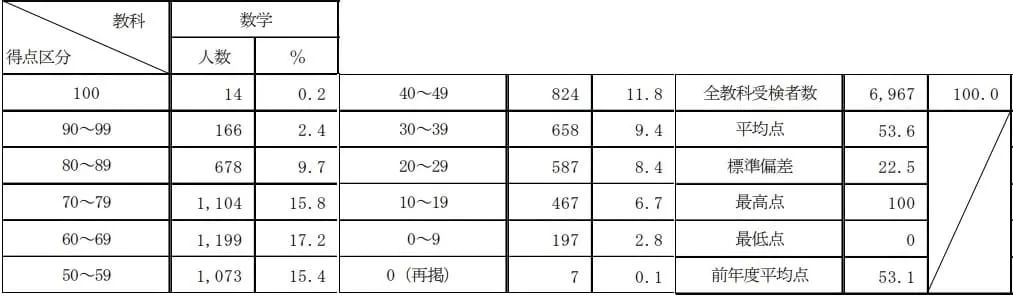
平均53.6点（前年比；＋0.5点）

問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）ア　98.2％
４－10
＝－６

イ　89.9％
（－２）²×３＋（－15）÷（－５）
＝４×３＋３
＝15

ウ　66.0％
６ｘ²－ｘ－５
－)２ｘ²＋ｘ－６
４ｘ²－２ｘ＋１

エ　79.4％
（６ｘ²ｙ＋４ｘｙ²）÷２ｘｙ
＝６ｘ²ｙ÷２ｘｙ＋４ｘｙ²÷２ｘｙ
＝３ｘ＋２ｙ

オ　48.4％
√（３/２）－√54/２
＝√６/２－３√６/２
＝－√６

（２）　59.8％
縦がｘ、横がｙ。
２（ｘ＋ｙ）は縦と横の長さを２倍した数→長方形の周の長さ

（３）
●相対度数●　72.9％
６÷20＝６/20＝30/100＝0.30
●累積相対度数●　60.9％
（４＋６＋１）÷20＝0.55

（４）　55.1％
３ｘ²－６ｘ－45
＝３（ｘ²－２ｘ－15）
＝３（ｘ＋３）（ｘ－５）

（５）ａ…53.7％、ｂ…47.4％
『ｘが２増加するとｙが４増加』→変化の割合（傾きａ）＝４/２＝２
ｙ＝２ｘ＋ｂに（１、－３）を代入。
－３＝２＋ｂ
ｂ＝－５
ａ…２、ｂ…－５

（６）　76.1％

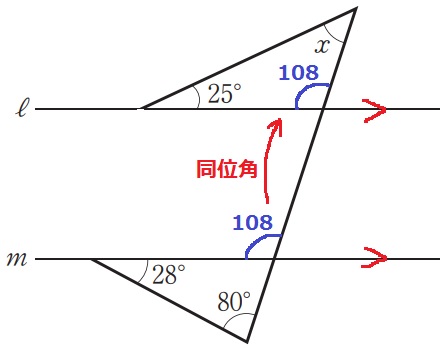
外角定理を用いて、28＋80＝108°
同位角で108°をあげる。
ｘ＝180－（25＋108）＝47°

（７）　45.0％

ＢＤで分割すると有名三角形が現れる。
△ＡＢＤは直角二等辺。辺の比は１：１：√２だから、ＢＤ＝４√２×√２＝８ｃｍ
△ＢＣＤは辺の比が１：２：√３の直角三角形。ＢＣ＝８×√３/２＝４√３ｃｍ

（８）　35.5％
ア：第２四分位数は中央値（メジアン）のこと。〇
イ：四分位範囲＝第３四分位数－第１四分位数
中央に集まる約50％のデータで、極端にかけ離れた外れ値の影響を受けにくい。〇
ウ：箱の長さは四分位範囲を表す。×
範囲（レンジ）＝最大値－最小値
エ：四分位範囲は中央値から±25％、全体の約50％のデータ。〇
ウ

大問２（作図・確率）

（１）　51.6％

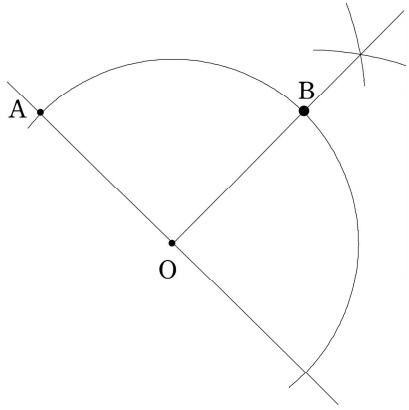
『時計回りに90°』だから、Ａの右側にＢがある。
ＡＯを延長、Ｏを通る垂線をひく。
半径ＯＡの長さをとって垂線に移す。交点がＢ。

（２）ア　あ…71.8％、い…56.5％、う・え…79.4％、Ｘ…83.8％
３桁の整数は、５×４×３＝60通り（あ）
最も大きい百の位で場合分けをする。（Ｘ＝百）
もしくは、うしろのレンのセリフでＸの位は３、（う）、（え）の３パターンしかない点から、
Ｘは百の位と確定することができる。

百の位が３のとき、350位以上の整数だから十の位は５で確定。
一の位は残りの１、２、４→３通り（い）
百の位は３の他に４（う）か５（え）
あ…60、い…３、う…４、え…５、Ｘ…百

イ　54.1％
●百の位が３●
前問より３通り。

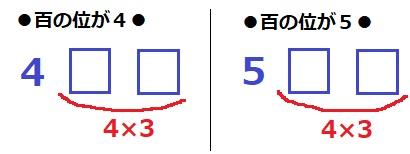
残りの枚数から、おのおの４×３＝12通り
350以上の整数は、３＋12＋12＝27通り
確率は27/60＝９/20

大問３（平面図形）

（１）ア　66.0％

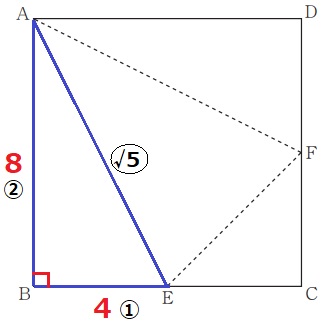
△ＡＢＥで三平方。
ＡＢ：ＢＥ＝②：①なので、辺の比で三平方を使うとＡＥ＝〇√５
ＡＥ＝４√５ｃｍ

イ（ア）　19.7％！

直角を意識して組み立てると、Ｂ、Ｃ、Ｄが一致し、
底面は直角二等辺三角形、高さ８ｃｍの三角錐になる。
体積は、４×４÷２×８÷３＝64/３ｃｍ³

（イ）　6.4％!!
展開図より△ＡＥＦの面積は、８×８－（４×８÷２×２＋４×４÷２）＝24ｃｍ³
これを底面とした高さは、64/３×３÷24＝８/３ｃｍ

（２）ア　あ…67.9％、い…64.5％、う…70.5％
△ＤＦＢ≡△ＤＨＥの証明。

誘導に従う。
△ＤＢＥは直角二等辺三角形。ＤＢ＝ＤＥ
四角形ＤＦＧＨは正方形だから、ＤＦ＝ＤＨ
リード文より、斜辺と他の１辺が等しい直角三角形で△ＤＡＦ≡△ＤＣＨ（★）
対応する角は等しく、∠ＡＤＦ＝∠ＣＤＨ（×）

∠ＢＤＦ＝45－∠ＡＤＦ（×）、∠ＥＤＨ＝45－∠ＣＤＨ（×）なので、
∠ＢＤＦ＝∠ＥＤＨ（●）
２辺とあいだの角が等しいから△ＤＦＢ≡△ＤＨＥ
あ…ＤＦ＝ＤＨ　い…∠ＢＤＦ＝∠ＥＤＨ　う…２辺とあいだの角

イ　12.4％！

正方形の１辺から、ＡＢ＝ＡＤ＝５ｃｍ
前述の証明にあった△ＤＡＦ≡△ＤＣＨより、対応する辺でＡＦ＝ＣＨ＝２ｃｍ
●＋×＝90°で等角を調べると、２角相等で△ＤＡＦ∽△ＦＢＩ
ＢＩ＝２×３/５＝６/５ｃｍ
△ＦＢＩの面積は、６/５×３÷２＝９/５ｃｍ²

大問４（関数）

（１）ア　81.6％
ｙ＝１/２ｘ²にｘ＝２を代入する。
ｙ＝１/２×２²＝２

イ　60.9％
『Ａ、Ｂの距離が６ｃｍ』→Ａのｙ座標は６
ｙ＝ａｘ²は（２、６）を通過する。
６＝４ａ
ａ＝３/２

（２）ア　32.6％！

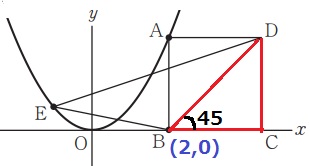
ＢＤは正方形ＡＢＣＤの対角線→△ＢＣＤは直角二等辺
ＢＤの傾きは１。
切片はＢから左に２、下に２だから－２。
ｙ＝ｘ－２

イ　2.1％!!

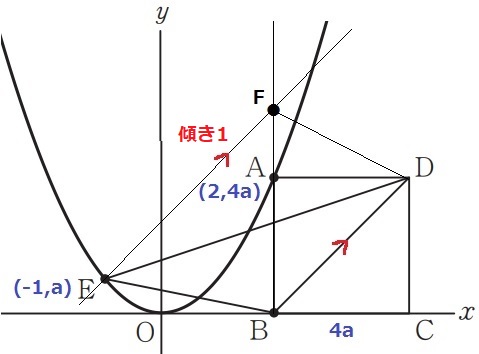
ｙ＝ａｘ²にそれぞれのｘ座標を代入。
Ａ（２、４ａ）Ｅ（－１、ａ）
正方形ＡＢＣＤの１辺で、ＢＣ＝４ａｃｍ

Ｅを通るＢＤに平行な線をひき、ＢＡの延長との交点をＦとする。
等積変形で、△ＢＤＥ＝△ＢＤＦ＝80ｃｍ²

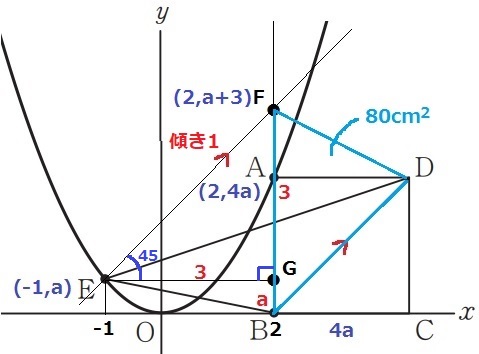
ＥからＦＢに向けて垂線をおろし、足をＧとする。
ＥＦの傾きはＢＤと同じ１。
→∠ＦＥＧ＝45°、∠ＥＧＦ＝90°から、△ＥＧＦは直角二等辺。
ＥＧ＝ＦＧ＝３ｃｍ
ＦＢ＝ＧＢ＋ＦＧ＝ａ＋３ｃｍ

△ＢＤＦの面積で等式を立てる。
（ａ＋３）×４ａ÷２＝80
２ａ²＋６ａ－80＝０　←÷２
ａ²＋３ａ－40
＝（ａ＋８）（ａ－５）＝０
ａ＞０だから、ａ＝５

大問５（方程式）

（１）あ　66.0％
一次方程式。
りんごａ個。なしは残りの50－ａ個。　

い　55.6％
連立方程式。
全体の個数で等式。
ａ＋ｂ＝50
値段で等式。
120ａ＋150ｂ＋40＝6700

（２）ア　21.9％！
りんご120円が（ｘ＋18）個、なし150円が（ｙ＋18）個。
これに箱代40円を足す。
う：120（ｘ＋18）＋150（ｙ＋18）＋40

イ　え…26.0％！、お…8.7％!!
４ｘ＋５ｙ＝60
ｙについて解くと、
５ｙ＝－４ｘ＋60
ｙ＝－４/５ｘ＋12
分母が５なので、ｙが整数になるのはｘ＝５のときｙ＝８

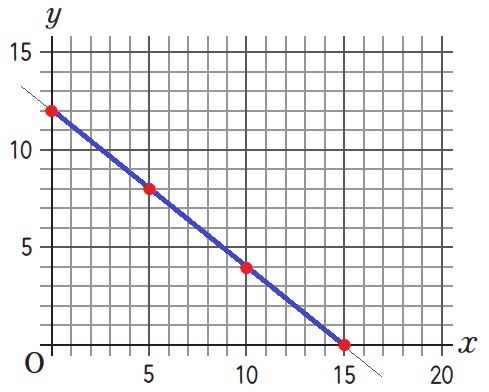
傾きは－４/５だから、右に５いくと下に４移動する。
（５、８）から格子点を調べると、他は（０、12）（10、４）（15、０）
え：（０、12）（５、８）（10、４）（15、０）

ここで一次不等式を使います。。
りんごを（ｘ＋18）個、なしを（ｙ＋18）個とおいたので、
条件Ｂより、（ｘ＋18）＋（ｙ＋18）＞50
ｘ＋ｙ＞14
４組のうち、ｘ＋ｙが15以上は（15、０）のみ。
りんご…15＋18＝33個
なし…０＋18＝18個
お：（15、０）、りんご…33個、なし…18個

＠別解＠
４ｘ＋５ｙ＝60
60は４の倍数だから、（ｘ、ｙ）＝（15、０）が決まる。
係数の４と５は互いに素→最小公倍数20（４×５＝５×４）で交換できる。
つまり、ｘを５減らしてｙを４増やせば帳尻が合う。
（15、０）（10、４）（５、８）（０、12）