平均11.6点（前年比；＋0.8点）
問題はコチラ→ＰＤＦファイル
Ｂグループの解説はコチラ。
出題範囲の削減はないが、基礎的・基本的な事項をより重視して出題。
大問１（小問集合）
（１）
５－（－６）÷２
＝５＋３＝８
（２）
（３ｘ－２）/４－（ｘ－３）/６
＝｛３（３ｘ－２）－２（ｘ－３）｝/12
＝（９ｘ－６－２ｘ＋６）/12
＝７/12ｘ
（３）
３/√２－２/√８
＝３√２/２－√２/２
＝√２
（４）
（２ｘ＋１）2－（２ｘ－１）（２ｘ＋３）
＝４ｘ2＋４ｘ＋１－４ｘ2－６ｘ＋２ｘ＋３
＝４
（５）
真ん中の数をｎとすると、連続する３つの自然数は、ｎ－１、ｎ、ｎ＋１。
（ｎ－１）2＋ｎ2＋（ｎ＋１）2
＝３ｎ2＋２＝365
ｎ2＝121
ｎ＝11
もっとも小さい数であるｎ－１は10。
（６）
比例は一次関数。
ア：ｙ＝ｘ3 ×
イ：ｙ＝50/ｘ ×
ウ：ｙ＝２πｘ 〇
エ：ｙ＝0.05ｘ 〇
ウ・エ
（７）
『少なくとも１人は当たり』→全体から２人ともハズレを引く。
Ａは５本から３本あるハズレをひき、Ｂは残った４本から２本あるハズレを引く。
２人ともハズレ…３/５×２/４＝３/10
少なくとも１人は当たり…１－３/10＝７/10
（８）
反比例はｘｙの積が比例定数ａで一定。
ａ＝４/５×15＝12
積が12となる２つの正の整数の組み合わせを数える。
（１、12）（２、６）（３、４）（４、３）（６、２）（12、１）
６個
（９）
３ｘ－５＝－２ｘ＋５
ｘ＝２
ｙ＝３ｘ－５に代入。
ｙ＝３×２－５＝１
（２、１）
（10）
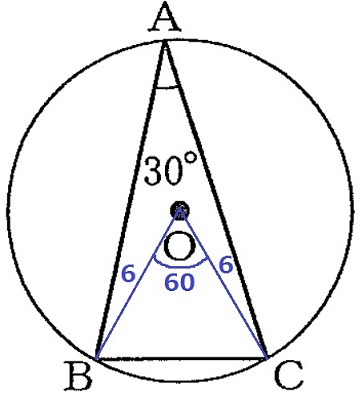
中心角は円周角の２倍。
∠ＢＯＣ＝30×２＝60°
半径より、ＯＢ＝ＯＣ。
△ＯＢＣは頂角が60°の二等辺三角形⇒つまり、正三角形。
ＢＣ＝６ｃｍ
大問２（小問集合２）
（１）
ｙ＝１/４ｘ2にｙ＝９を代入してＡ（６、９）
ｘ＝－４を代入してＢ（－４、４）
Ｃ（０、９）
△ＯＢＣの面積…９×４÷２＝18
△ＯＡＣの面積…９×６÷２＝27
四角形ＣＢＯＡの面積は18＋27＝45だから、その半分は22.5。
↑このようなＣＤで区切れば、左右が22.5で二等分になる。
ＯＤ：ＤＡ＝4.5：22.5＝①：⑤
Ｄの座標はＡから求める。
（６÷６、９÷６）＝Ｄ（１、３/２）
ＣＤの変化の割合は、（３/２－９）÷（１－０）＝－15/２
切片はＣのｙ座標である９だから、ＣＤ；ｙ＝－15/２ｘ＋９。
（２）
ｘとｙ以外のシュートの本数の合計を調べる。
０×０＋１×１＋２×２＋４×３＋５×２＋７×２＋８×３＋９×１＋10×１＝84本
120－84＝36本
３ｘ＋６ｙ＝36
ｘ＋２ｙ＝12
ｘ＝－２ｙ＋12
ｘとｙの組み合わせを調べる。
ｙで場合分けするといい。自然数なので０は含まない！
（ｘ、ｙ）＝（10、１）（８、２）（６、３）（４、４）（２、５）
以上、５組。
シュートを入れた本数の最頻値（モード）は６本だから、
（ｘ、ｙ）＝（２、５）
*（４、４）だと最頻値が同数になってしまうので×！
Ａ…－２ｙ＋12、ａ…５、ｂ…２、ｃ…５
（３）①
最初の２周（600ｍ）を４分で走る。
Ｓ地点で３分休憩(๑´ㅂ`๑)🍵
残りの３周（900ｍ）を９分で走る。
②
先ほどのグラフに書き込むのかと思いきや、
実際は１本道ではなく、池の周りを周回するのでグラフの形を変える。
Ａの休憩が終わった７分～16分後を考える。
縦軸は１周300ｍ。上の300ｍが下の０ｍ、すなわちＳ地点と同じ。
一番上に到達したら一番下に戻るを繰り返す。
Ｂは５周を６分で走る→１周あたり1.2分で走る。
これを９分後から図で示すと、Ａを３回追い抜く。
大問３（図形）
（１）
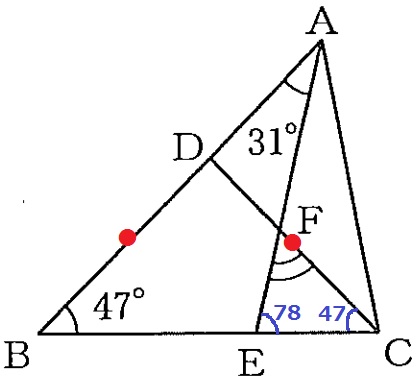
△ＤＢＣは二等辺→∠ＤＣＢ＝47°
△ＡＢＥで外角定理→∠ＡＥＣ＝31＋47＝78°
△ＣＥＦの内角で、∠ＥＦＣ＝180－（78＋47）＝55°
（２）①
△ＥＢＣで三平方→ＥＢ＝２√10ｃｍ
②
出し方は複数ある。
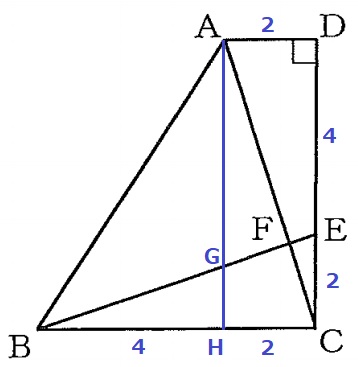
ＡからＢＣに向けて垂線をひき、
ＢＥ、ＢＣとの交点をそれぞれＧ・Ｈとする。
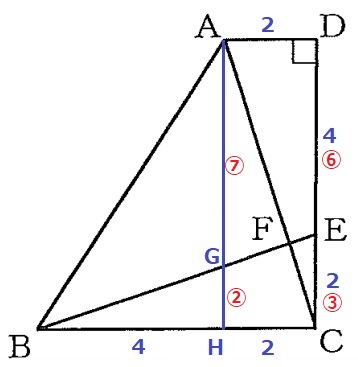
△ＧＢＨ∽△ＥＢＣより、ＧＨ：ＥＣ＝ＢＨ：ＢＣ＝②：③
ＤＥはＥＣの２倍だから、ＤＥ＝③×２＝⑥
ＡＨ＝ＤＣ＝⑨
ＡＧ＝⑨－②＝⑦
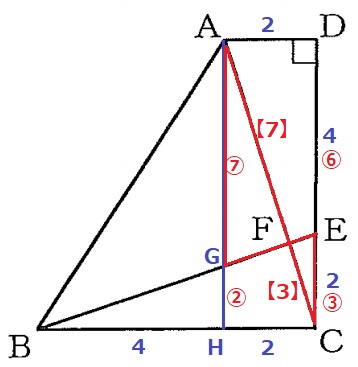
△ＡＧＦ∽△ＣＥＦより、ＡＦ：ＦＣ＝ＡＧ：ＣＥ＝【７】：【３】
△ＡＢＦ＝△ＡＢＣ×【７】/【10】＝６×６÷２×７/10＝63/５ｃｍ2
*初見では思いつきにくいですが、中学受験に出てくる解法です。
（３）①
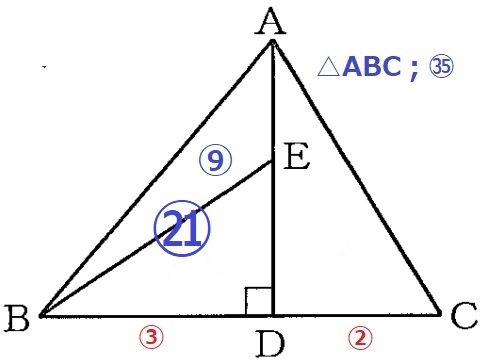
△ＡＢＤの面積…㉟×③/⑤＝㉑
ＡＥ：ＡＤ＝△ＡＢＥ：△ＡＢＤ＝⑨：㉑＝３：７
ＡＥはＡＤの３/７倍。
②
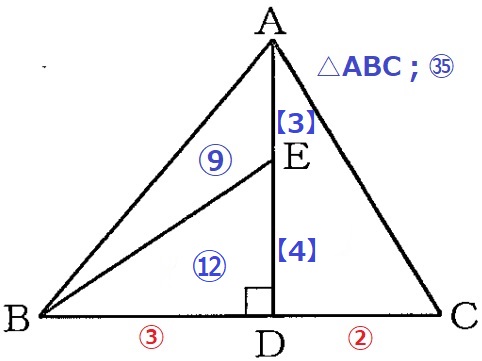
△ＡＢＥをＡＤを軸に回転させる。
底面は半径③の円、高さは【７】－【４】＝【３】の円錐。
△ＡＤＣをＡＤを軸に回転させる。
底面は半径②の円、高さは【７】の円錐。
③×③×π×【３】×１/３：②×②×π×【７】×１/３ ←πと１/３が共通するので削除。
＝27：28
したがって、27/28倍。
大問１
（３）分母の√８を２√２に変換して約分→有理化の流れでもＯＫ。
（５）真ん中をｎとおくと式がややスッキリする。最後にｎ－１を求める。
（６）比例は一次関数の仲間。
大問２
（１）面積比→辺の比。
（２）誘導がありがたい。他県では誘導なしバージョンもある。
（３）②周回のダイヤグラムを作成する。情報整理の仕方をおさえておきたい。
大問３
（２）②図形の演習問題に載っている形である。
他には、△ＡＣＤと△ＥＢＣが合同で、台形から２つの直角三角形を引き、重複する△ＥＣＦを足してもできる。△ＥＣＦは直角三角形と相似で斜辺の比から面積比が10：１とでる。
（３）比の扱いに慣れておきたい。
公立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
