2017年度　茨城県公立高校入試問題過去問【数学】解説

平均54.1点（前年比；＋5.2）
全体的に基本～標準です。
問題の種類が多いので前半部分はケアレスミスなしでいきたい。
問題ＰＤＦ

大問１（計算）

（１）
６－８
＝－２

（２）
－２²×３ー３×（－６）
＝－４×３＋１８
＝６

（３）
７/５÷（ー７/４）＋９/５
＝－４/５＋９/５
＝１

（４）
－２（ｘ＋３ｙ）＋（ｘ－ｙ）
＝－２ｘ－６ｙ＋ｘーｙ
＝－ｘ－7ｙ

（５）
８/√２＋３√６÷√３
＝４√２＋３√２
＝７√２

大問２（小問集合）

（１）因数分解。
ｘ^２－６ｘ－２７
＝（ｘ－９）（ｘ＋３）

（２）連立方程式。
後半の式を２倍して加減法でも良いし、
ｘ＝２ｙ＋６で代入法でも良い。
ｘ＝２、ｙ＝－２

（３）解の公式。
ｘの係数が偶数なのでｂ’バージョンを使うとショートカット。
ｘ＝－４±√１０

（４）
抜かれた水の量は３ａ、残りは２００－３ａ
２００－３ａ＜ｂ

（５）
ｘ²－２ｘ＋１＝（ｘ－１）²と因数分解してから代入する。
（ｘ－1）^２＝（√５＋１－１）^２＝√５²＝５

大問３（小問集合２）

（１）
等しい辺に印をつけておこう。半径は同じ長さ。
ＯＣ＝ＯＡから△ＯＣＡは二等辺。∠ＣＡＯ＝２３°
外角定理から∠Ｏ’ＯＡ＝２３＋２３＝４６°
Ｏ’Ｏ＝Ｏ’Ａから△Ｏ’ＯＡは二等辺。∠ＯＡＯ’＝４６°
∠ＣＡＢは半円の弧に対する円周角なので９０°
∠ＢＡＯ’＝９０－（２３＋４６）＝２１°

（２）
Ｂ＝Ａ＋５０、Ｃ＝Ａ＋１００、Ｄ＝１２０に置き換える。一次式
Ａ＋（Ａ＋５０）＋（Ａ＋１００）＋１２０＝５４０
３Ａ＋２７０＝５４０
３Ａ＝２７０
Ａ＝９０
Ｃ＝Ａ＋１００＝９０＋１００＝１９０ｇ

（３）
全体・・５×５＝２５通り
積が奇数ということは奇数×奇数しかない。
奇数同士は、２通り×２通り＝４通り
確率は、４/２５

大問４（関数）

（１）
Ａ（２、８）Ｄ（－２、２）を通る直線の式を求める。
Ｄ→Ａは、右に４上に６→傾きは６/４＝３/２
ｙ＝ａｘ＋ｂにあてはめて切片ｂを求める。
ｙ＝３/２x＋５

（２）
ＤＥ：ＥＣがわかればいい。
△ＡＣＥの面積を②、四角形ＡＢＣＤの面積を⑤とおけば、
四角形ＡＢＤＥの面積は③となる。

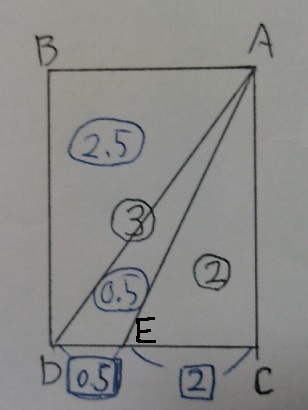
対角線ＡＤをひき、△ＡＢＤは長方形の半分なので〇２．５。
△ＡＤＥは、③－〇２．５＝〇０．５
ＤＥ：ＥＣ＝０．５：２＝１：４
ＤＣ＝４だから、ＤＥ＝４×１/５＝４/５
Ｅのｘ座標は－２＋４/５＝－６/５
ＤＣはｘ軸を並行でｙ＝２だから、Ｅ（－６/５、２）

大問５（平面図形）

（１）図形の証明
共通角と、平行線から同位角→２角が等しい
ベーシックで記述も短いから正解率は高い。

（２）
前問の△ＡＥＦ∽△ＡＢＤとＥＦ//ＢＤから
ＡＥ：ＥＢ＝ＡＦ：ＦＤ＝１：1（ＦはＡＤの中点）
ＣＨ：ＨＦ＝△ＣＨＢ：△ＦＨＤ＝ＢＣ：ＤＦ＝２：1
ＤＥとＣＢを延長した交点をＩとする。
ＣＧ：ＧＦ＝△ＣＧＩ：△ＦＧＤ＝ＣＩ：ＥＤ＝４：１
ＣＨ：ＨＧ：ＧＦで連比をする。
ＣＨ：ＨＧ＝５：１

＠別解＠
△ＣＨＢ：△ＦＨＤ＝２：１まで出す。
ＢＨ＝②、ＨＤ＝①
対角線ＢＤ＝③
△ＡＢＤで中点連結定理からＥＦ＝〇１．５
ＨＧ：ＧＦ＝△ＨＧＤ：△ＦＧＥ＝ＨＤ：ＦＥ＝①：〇１．５＝□２：□３
ＣＨ：ＨＦ＝△ＣＨＢ：△ＦＨＤ＝２：１だから、
ＣＨ＝ＦＨ×２＝□５×２＝□10
ＣＨ：ＨＧ＝□10：□２＝５：１
延長線と連比なしでも解答可。

大問６（数量変化）

（１）
１５分で８ｋｍ進むから、６０分で３２ｋｍ進む。
時速３２ｋｍ

（２）
ダイヤグラムに太郎を書き込む。
問題文の例示でいえば、駅７時０ｋｍから６０分空港８ｋｍまでの斜線をひく。
すると、駅から出発するバス（右上の線）に２回追い越され、空港を出発するバス（左下の線）と４回すれ違う。
空港から駅に向かうバスと３回すれ違うには、空港ギリギリで３回目のすれ違いがある【３０分８ｋｍ以上】と４回目のすれ違い寸前の【５０分８ｋｍ未満】の間となる。
３０分で８ｋｍ→６０分で１６ｋｍ
５０分で８ｋｍ→６０分で４８/５ｋｍ
４８/５の方が１６より小さい！速度が遅いから傾きも緩くなる。
時速４８/５ｋｍ以上～時速１６ｋｍ未満

大問７（データの活用）

（１）
ｘの値（ｂの平均値）をがんばって求める。
（７６＋９５＋３６＋４８＋５６＋４９）÷６＝６０→弁当Ｂの平均値が大きい。
木曜はＡＢ共に４８だが相対度数は異なる。木曜/総和
弁当Ａ：４８/（５６×６）＝１/７
弁当Ｂ：４８/（６０×６）＝２/１５
通分した方が速い。弁当Ａの方が大きい。
ａ：ウ　ｂ：ア

（２）
平均値が０．５上がったということは、総和は０．５×６＝３個増えた。
どこかの曜日が＋３となる。中央値６３を考える。
弁当Ｃの販売個数を小さい順に並び替えて整理
【３１、４２、５６、６８、７０、９３】
訂正前の中央値は、５６と６８の平均値である６２。
中央値が６３に変わったということは、５６か６８あたりが怪しい。
試しに５６→５９にすると中央値は６３．５となり不適。
６８→７１にすると順番が入れ替わり、中央値は５６と７０の平均で６３〇
水曜日に６８が７１となる。
水曜日７１個

大問８（図形）

（１）
折りたたんだときに接する辺は同じ長さ。
ひし形の１辺は等しくＡＦ＝ＡＥでもあるから、
ＡＢ＝ＢＦ＝ＡＣ＝ＣＥ
あとは面積比。△ＡＢＣ＝①とおくと、△ＡＥＦ＝④
ひし形ＡＥＤＦ＝⑧
１/８倍

（２）
ポイントは△ＡＧＤ
ひし形の１辺を求める。
ＦＨ＝３、ＨＤ＝４から△ＦＨＤは３：４：５の直角三角形
→ＦＤ（ひし形１辺）＝５ｃｍ
組み立てたときのＡＧ＝５ｃｍとなる。
△ＡＥＦ：△ＡＣＢ＝１：２なので、ＡＨ＝４からＡＧ＝２ｃｍ
ＧＤ＝ＡＤ－ＡＧ＝８－２＝６ｃｍ
組み立てたときの△ＡＧＤに着目する。
ＧＨ＝ｘとおく。ＨＤ＝６－ｘ
△ＡＧＨと△ＡＤＨで、ＡＨを共通辺とした三平方。
２²－ｘ²＝５²－（６－ｘ）²
４－ｘ²＝２５－３６＋１２ｘ－ｘ²
１２ｘ＝１５
ｘ＝５/４
△ＡＧＨで三平方
ＡＨ＝√{２²－（５/４）²}
＝√（４－２５/１６）
＝√（３９/１６）
＝√３９/４ｃｍ