2017年度　埼玉県公立高校入試【数学】解説

平均４４．４点

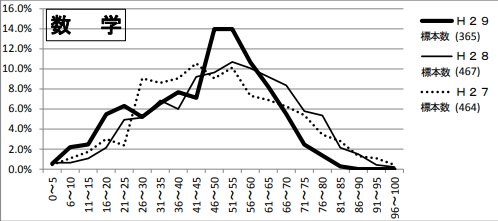
学校選択ではない方です。
できるところは手早く処理して、難しい問題に時間を残しておきましょう。
問題はコチラから→ＰＤＦファイル

大問１（小問集合）

（１）　98.9％
１０ｘ－７ｘ＝３ｘ

（２）　97.3％
（－２）×４＋１
＝－８＋１＝－７

（３）　62.9％
９ａ²÷３ａｂ×（－ｂ）
＝－３ａ

（４）　72.4％
√８＋２/√２
＝２√２＋２√２/２
＝２√２＋√２＝３√２

（５）　77.7％
Ｘ²－１３ｘ＋３６
＝（ｘ－４）（ｘ－９）

（６）　86.7％
連立方程式、
２つ目の式を３倍してｙを消すのがやりやすいかな？
ｘ＝－１、ｙ＝２

（７）　66.3％
（ｘ＋４）²－５＝０
（ｘ＋４）²＝５
ｘ＋４＝±√５
ｘ＝－４±√５
一度かっこ内を展開して、解の公式を利用してもいい。
ｂ’公式だと若干ショートカットできる。

（８）　48.8％
ℓ＝２（ａ＋ｂ）
ℓ＝２ａ＋２ｂ
２ｂ＝ℓ－２ａ
ｂ＝（ℓ－２ａ）/２（＝ℓ/２－ａ）

（９）　76.5％
時間＝道のり÷速さ。シンプル過ぎて逆にビビる。
ｙ＝1500/ｘ

（10）　31.2％！
グラフ上でａ≦ｘ≦ａ＋２をイメージしながら代入してみる。
y＝０ということは原点に触れていなければならない。
ｙ＝４はｘ＝－２か２に触れていなければならない。
ア・ウ

（11）　61.5％
３種類→ＡＢＣが３つ異なる→３×２＝６通り
２種類→ＡＣが同じ、Ｂだけ異なる→ＡＣ３通り×Ｂ２通り＝６通り
６＋６＝１２通り

（12）　1.9％!!
平行四辺形の横の辺の長さがわかっていない。
縦の長さから相似をつかって横方向の辺の比を見つける。
△ＥＢＦ：△ＣＦＤ＝ＥＢ：ＣＤ＝６：１０＝３：５
よって、ＥＦ：ＦＣ＝３：５
ＥＧ：ＧＢ＝３：５
ＥＧ＝６×３/８＝９/４ｃｍ

大問２（小問集合２）

（１）　23.8％！
千葉の作図より楽チン。
円周角の定理を用いる。直径に対する円周角は常に直角である。
ＡＢを直径とする円を描き、円周とℓの交点がＰとなる。

（２）　34.0％
わかりやすい最頻値からウを除外。
40人の中央値は20人目と21人目の平均。地道に足して調べていく。
イの中央値は８となり不適。平均値を求める。
ア：（６×１＋７×５＋８×14＋９×９＋10×11）÷20＝8.6点×
エ：（４×１＋６×２＋７×４＋８×13＋９×12＋10×８）÷20＝8.4点〇

（３）　1.3％!!
シンプルな図形だが一筋縄ではいかない。
扇形があるので半径を知りたいところだが、ちょっと迂回する必要がある。
ＡＯとＢＯに補助線。△ＡＯＤ≡△ＡＯＥ、△ＢＯＥ≡△ＢＯＣとなる。
理由は台形の１内角と円の接線から直角で、ＡＯとＢＯは共通辺で各々の直角三角形の斜辺となる。
円の半径は等しいから、直角三角形の合同条件である斜辺と他の１辺が等しくなるから。
ＡＢ＝３＋９＝１２ｃｍ
ＤＡを延長、ＢＣに垂直な線分で、これらの交点をＦとする。

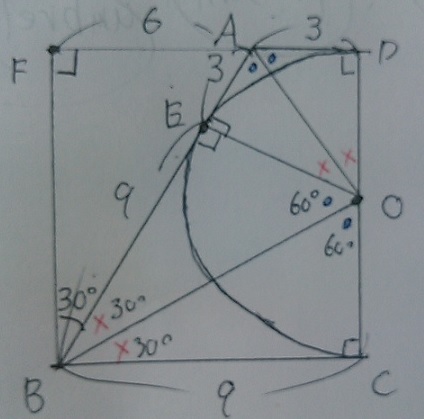
△ＡＦＢで三平方。これで台形の高さＤＣの長さが６√３ｃｍとわかる。
扇形の中心角である∠ＥＯＣを求めたい。
△ＡＦＥは１：２：√３の直角三角形なので∠ＡＢＦ＝３０°
∠ＥＢＣ＝６０。前述の合同から等しい角に印をつけていくと∠ＥＯＣ＝１２０°となる。
あとは、四角形ＥＢＣＯ（直角三角形×２）から中心角１２０°の扇形をひけばいい。
９×３√３÷２×２－３√３×３√３×π×120/360＝２７√３－９πｃｍ²

*中心角∠ＥＯＣの求め方だが、四角形ＥＢＣＯはＢＯを直径とする円に内接するので、
内接する四角形の対角の和は１８０°だから、１８０－６０＝１２０°でもいける。

（４）　12.5％！
ｘみたいな展開図をいじっていく。
組み立てたときの正四角柱の高さを①、底面の1辺の長さを②とする。

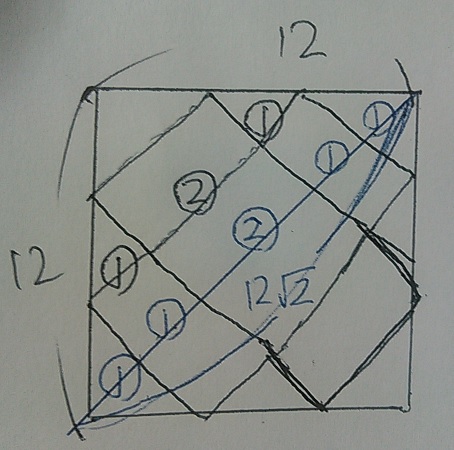
端っこの①は、1辺が①の正方形や直角二等辺三角形で考えてみて下さい。
大きな正方形の対角線は1：1：√2から12√２ｃｍ
これが⑥だから、①＝１２√２×１/６＝２√２ｃｍ

大問３（証明）

（１）　51.3％
問題集によく載ってるタイプ。確実に正解したいところ。

（２）①　54.3％
連続する素数の差が２である双子素数。
表の素数に○つけて調べる。

②　0.5％!!!
普通、整数の証明では、なんとかをなんとかｎにおいて・・・、＝３（ｎ・・・）みたいに文字式を使うのが定石だが、本問は全く文字式を使わなくても良い。
やり方はＡさんの説明を参照する。素数は偶数ではない＝奇数であることから、双子素数（差が２の素数のペア）に挟まれた数は偶数であると説明した。双子素数＋間の数は連続する３つの整数なので、連続する３つの整数には必ず３の倍数であることを指摘すれば、素数が３の倍数でない以上、あいだの数が３の倍数となる。
①で調べた間の数は１８、３０、４２と全て６の倍数になっている。
これは２の倍数×３の倍数＝６の倍数だから。
学校選択問題では、２の倍数と３の倍数を自力で解説してから６の倍数の証明まで要求している。

大問４（関数）

（１）４ｃｍ²　50.9％
*等積変形。４×２÷２＝４ｃｍ²

（２）ａ＝１/４　22.5％！
*傾きを求める設問だが、ＡとＢのｙ座標が不明であることから戸惑った受験生はいたかもしれない。
座標もａで表す。Ａ（－２、４ａ）Ｂ（４、１６ａ）
右に６で上に１２ａだから、直線ＡＢの傾きは２ａ
これを一般式に代入。
Ｃ（０、２）から切片２はわかっているので、ａだけを求めればよい。
４ａ＝－２×２ａ＋２
４ａ＝－４ａ＋２
８ａ＝２　　ａ＝１/４

（３）　0.9％!!!
配点７のうち途中式の書き込みでどこまで部分点がもらえるかは学校の裁量次第。
△ＢＤＥ∽△ＢＣＯから面積比を使う。
△ＢＤＥは△ＯＡＢの面積を４分の１する。
△ＢＣＯは（１）で出している。
面積比は辺の比の２乗。公式解答では新たな線分ｈをつくり、
△ＢＤＥ：△ＢＣＯ＝ｈ²：４²からｈを求め、Ｐのｘ座標を求めている。

学校選択問題では、辺ＢＥを回転の軸として△ＢＤＥを１回転させた立体の求積が出題された。
公立高校入試解説ページに戻る