2023年度　秋田県公立高校入試問題過去問【数学】解説

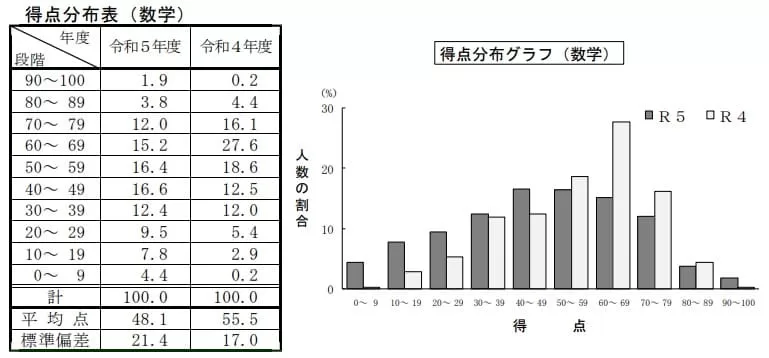
平均48.1点（前年比；－7.4点）

問題はコチラ→ＰＤＦファイル

大問１（小問集合）

*15問の中から指示された８問を解答する。
（１）　79.9％
８＋12÷（－４）
＝８－３
＝５

（２）　63.7％
12ａｂ÷６ａ²×２ｂ
＝４ｂ²/ａ

（３）　83.6％
４＝√16＞√10
４＞√10

（４）　70.4％
２（ｘ－５ｙ）＋５（２ｘ＋３ｙ）
＝２ｘ－10ｙ＋10ｘ＋15ｙ
＝12ｘ＋５ｙ　←ここで代入
＝12×１/２＋５×（－３）
＝６－15
＝－９

（５）　58.2％
√２/２－１/３√２
＝√２/２－√２/６
＝√２/３

（６）　61.9％
（５ｘ－２）/４＝７　←両辺×４
５ｘ－２＝28
ｘ＝６

（７）　85.8％
２ｘ＋ｙ＝５　…①
ｘ－４ｙ＝７　…②
①－②×２で、９ｙ＝－９
ｙ＝－１
①に代入、２ｘ－１＝５
ｘ＝３
ｘ＝３、ｙ＝－１

（８）　79.1％
ｘ²＋５ｘ＋２＝０
解の公式を適用して、ｘ＝（－５±√17）/２

（９）　17.6％！

１辺５ｃｍの正三角形をバラすと、外周は５×３×３＝45ｃｍ
１辺ａｃｍの正三角形は底辺が外周の重複部分で、他２辺は内部にある。
→45ｃｍから、３ａ×２＝６ａｃｍを引けばいい。
45－６ａｃｍ

（10）　11.3％！
231を素因数分解。231＝３×７×11
231の約数は１、３、７、11、３×７＝21、３×11＝33、７×11＝77、231の８個。
これらをｎ＋２とすると、ｎ＝－１、１、５、９、19、31、75、229
ｎは100より小さい素数だから、ｎ＝５、19、31

（11）　79.7％

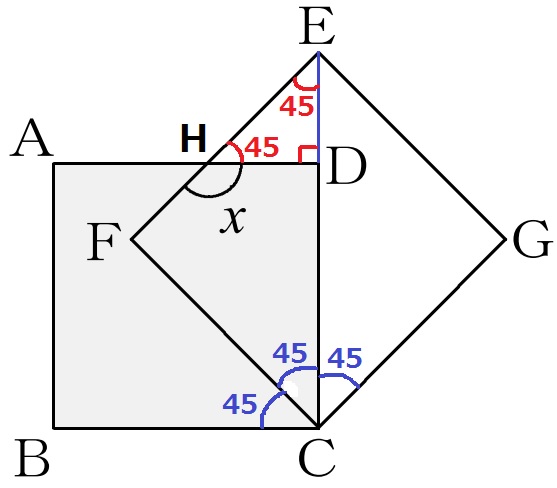
ＢＣを時計回りに45°回転させるとＦＣ。
∠ＦＣＤ＝45°だから、ＤＣは対角線ＥＣ上にある。
ＡＤとＥＦの交点をＨとすると、∠ＨＥＤ＝45°
△ＨＤＥは直角二等辺で∠ＥＨＤ＝45°
ｘ＝180－45＝135°

＠別解＠

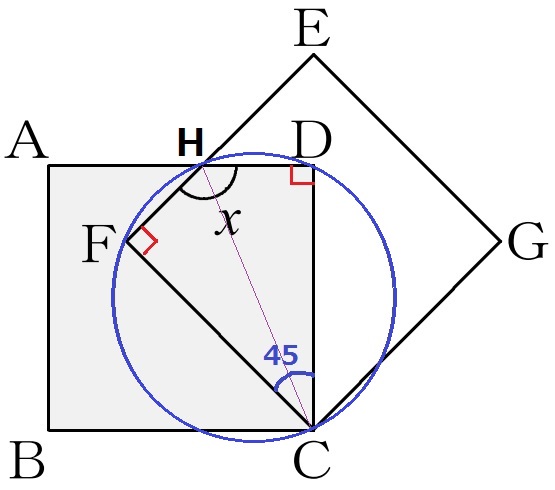
∠ＨＦＣ＝∠ＨＤＣ＝90°から、４点Ｈ・Ｆ・Ｃ・Ｄは直径ＨＣとする同一円周上にある。
内接する四角形の対角の和は180°だから、ｘ＝180－45＝135°

（12）　29.3％！

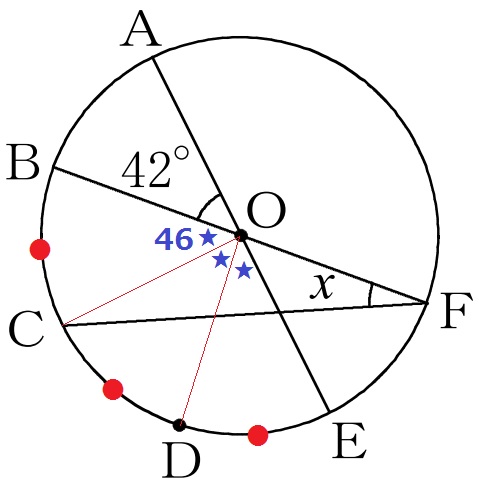
弧ＢＣ＝弧ＣＤ＝弧ＤＥから、３つの中心角（★）は等しい。
∠ＢＯＣ＝（180－42）÷３＝46°
この円周角が∠ＢＦＣだから、ｘ＝46÷２＝23°

（13）　49.1％

２角相等で△ＡＢＣ∽△ＤＡＣ。
ＡＤ＝12×６/８＝９ｃｍ

（14）　1.4％!!

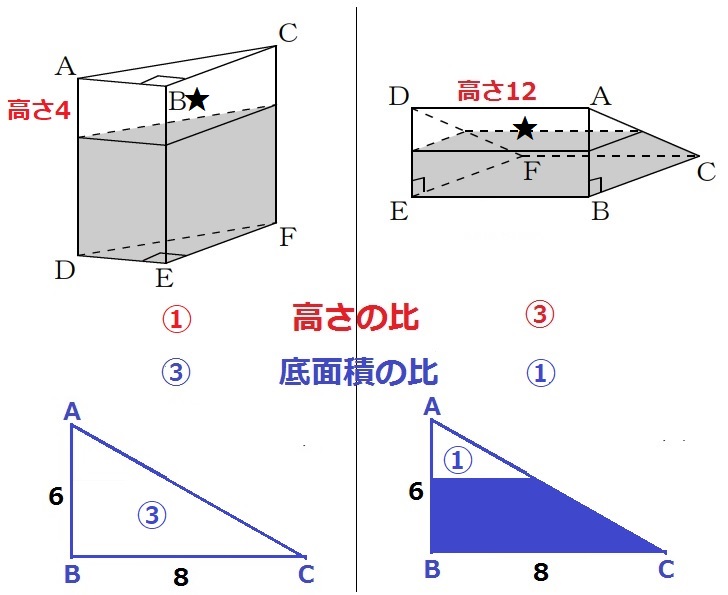
水の体積は変わらない⇒空気の部分の体積も変わらない。
空気の部分の高さの比は、４：12＝①：③
底面積の比は逆比で③：①。

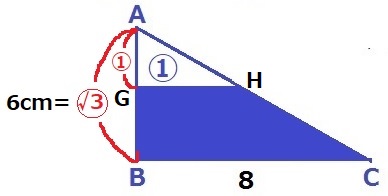
水面の両端をＧ、Ｈとする。
△ＡＧＨ：△ＡＢＣ＝①：③
相似比は、ＡＧ：ＡＢ＝①：〇√３
ＡＧ＝６×①/〇√３＝２√３ｃｍ
水面の高さＧＢ＝６－２√３ｃｍ

（15）　18.9％！

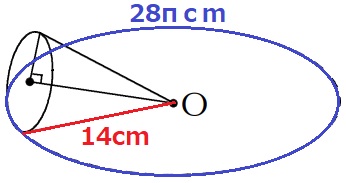
底面の円の円周は、４×２×π＝８πｃｍ
これが3.5周したから、円Ｏの円周は８π×3.5＝28πｃｍ
円Ｏの半径は、28π÷π÷２＝14ｃｍ→円錐の母線が14ｃｍ
円錐の側面積＝母線×半径×π
円錐の表面積は、４×４×π＋14×４×π＝72πｃｍ²

大問２（小問集合２）

（１）①　61.5％

休憩場所はちょうど駅と図書館の中間（1800ｍ地点）である。
前半と後半の速さの比は、60：120＝１：２
距離が等しければ、時間の比は逆比で２：１。
前半の移動が30分間だから、後半の移動は15分間。
50－15＝35分のときに休憩地点を発った（＝休憩時間は５分間）。

②　36.0％
健司は毎分60分、美咲は毎分240分で移動する。
両者は１分あたり300ｍ近づくので、3600÷300＝12分後に出会う。
（健司が休憩する前の時刻だから問題ない）
午前10時12分

（２）①　73.5％
取り出し方は全部で、３×３＝９通り
積が奇数は、奇数×奇数しかない。
積が奇数の組み合わせは（１、５）（３、５）の２通り。
確率は２/９。

②　38.5％

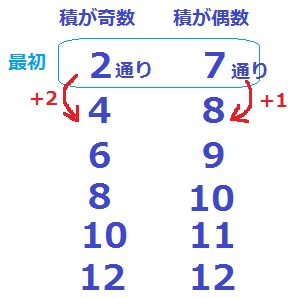
追加前の積が奇数は２通り、偶数は７通りだった。
袋Ｂに７を１枚入れると、奇数は（１、７）（３、７）、偶数は（２、７）が追加。
７を１枚入れるたびに積が奇数は２通り、偶数は１通り追加される。
追加前の差が７－２＝５通りで、１枚ごとに差が１通りずつ縮まるので、
５枚入れると奇数と偶数の場合の和が等しくなり、確率も等しくなる。
５枚

（３）　72.4％

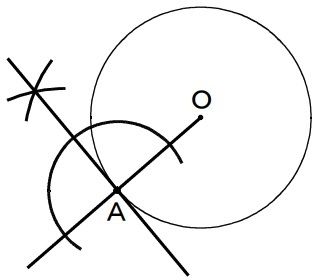
Ａを接点とする接線の作図。
半直線ＯＡでＡを通る垂線を描けばいい。

大問３（データの活用）

（１）　76.2％
最頻値（モード）は最もあらわれている値。
31人の中央値は16番目の値だが、最頻値が最も小さいイ（20-30分）を選べばいい。

（２）　38.9％
範囲（レンジ）＝最大値－最小値＝110－５＝105分
30人の第１四分位数は下位15人の真ん中、下から８番目の30分。
範囲…105分、第１四分位数…30分

（３）①　36.0％
ア：グループ２の第１四分位数は55分を超える。55分以下は多くても４人しかない。〇
イ：55分以下が最も少ないのはグループ２⇒55分以上が最も多いのはグループ２。×
少なくとも12人は55分以上である。
ウ：80～100分のグループ１と３はヒゲの部分で詳細不明。×
エ：最大値は100分以上だから、どのグループにもいる。〇
ア、エ

②　53.5％
説明問題。
四分位範囲＝第３四分位数－第１四分位数
箱の長さで、極端な値を除外した真ん中50％のデータの散らばり具合を表す。
範囲と四分位範囲が最も大きいグループ１がデータの散らばり具合が最も大きい。
ア

大問４（平面図形）

（１）　24.2％！
△ＡＣＥ≡△ＢＣＦの証明。

仮定から、ＣＥ＝ＣＦ
正三角形の１辺より、ＡＣ＝ＢＣ
正三角形の内角とＡＣ//ＥＣの錯角で、∠ＡＣＥ＝∠ＢＣＦ
２辺とあいだの角が等しいから合同。

（２）ア　42.7％
いきなり論理形式の問題が現れる。
『ａ＝３、ｂ＝６ならば、ａ＋ｂ＝９』
ならばの前が仮定、後ろが結論で、これらをひっくり返すと逆になる。
逆【ａ＋ｂ＝９ならば、ａ＝３、ｂ＝６】

イ
もとの命題が真（正しい）でも、逆は必ずしも真ではない。
先の逆であれば、ａ＝４、ｂ＝５の場合は成り立たない。
反例が１つでもあれば、偽（誤り）になる。
（１、８）（２、７）でもＯＫ。０は自然数ではない。

＠逆・裏・対偶＠

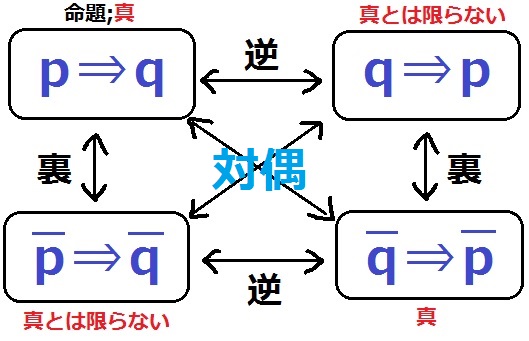
『ｐであるならば、ｑである』という命題に対して、
『ｑであるならば、ｐである』を逆といい、
『ｐでないならば、ｑではない』を裏という。（ｐやｑの上に￣がつく）
逆や裏は必ずしも真とは限らない。
『ｑでないならば、ｐではない』を対偶といい、
元の命題（ｐ⇒ｑ）が真ならば、対偶は必ず真である。

たとえば、【４の倍数であれば、２の倍数である】という真の命題に対して、
逆【２の倍数であれば、４の倍数である】
裏【４の倍数でなければ、２の倍数でない】は反例があるので偽である。
（６や10は４の倍数ではない２の倍数）
一方で、対偶【２の倍数でなければ、４の倍数でない】は真である。

（３）　13.3％！
３辺の関係性を示すと、
ＡＢ＝ＢＣ＋２、ＢＣ＝ＣＡ＋７
ＡＢ＞ＢＣ＞ＣＡなので、最も長いＡＢが斜辺である。

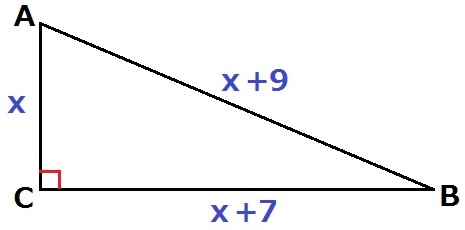
最も短いＡＣをｘｃｍとすると、ＢＣ＝ｘ＋７、ＡＢ＝ｘ＋９
ｘ²＋（ｘ＋７）²＝（ｘ＋９）²
ｘ²－４ｘ－32
＝（ｘ－８）（ｘ＋４）＝０
ｘ＞０より、ｘ＝８
斜辺ＡＢ＝ｘ＋９＝17ｃｍ

＠別解＠

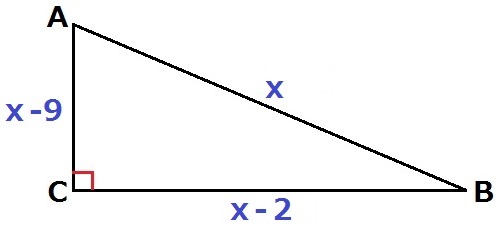
求めたいＡＢを直接ｘにおいても、もちろんできる。
ｘ²＝（ｘ－９）²＋（ｘ－２）²
ｘ²－22ｘ＋85
＝（ｘ－17）（ｘ－５）＝０
最も短いＡＣに着目して、ｘ－９＞０でなければならないからｘ＞９
よって、ｘ＝17→17ｃｍ

大問５―Ⅰ（関数）

（１）　40.1％
答案では求める過程も記述する。
Ａ（－１、１）→Ｂ（２、４）
右に３、上に３だから傾きは１。
切片はＡから右に１、上に１で１＋１＝２
ｙ＝ｘ＋２

（２）　26.4％！
ｙ＝２/３ｘ²にｘ＝３を代入。
ｙ＝２/３×９＝６
Ｂ（２、４）Ｃ（３、６）
ｘ座標の差が１、ｙ座標の差が２。
三平方の定理でＢＣ＝√５ｃｍ

（３）　3.9％!!
ｙ＝ａｘ²にあるＱのｘ座標が知りたい。

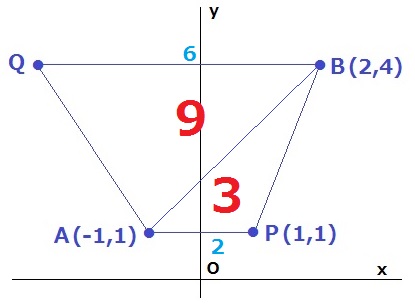
ｙ＝ｘ²にｙ＝１を代入、ｘ＞０からＰ（１、１）
ＡとＰ、ＱとＢはｙ座標が同じで、ＱＢ//ＡＰ
台形ＡＰＢＱをＡＢで分割する。
△ＡＰＢの面積は、２×３÷２＝３ｃｍ²
△ＡＢＱの面積は、12－３＝９ｃｍ²になる。
ＱＢ＝９×２÷３＝６ｃｍ

Ｑのｘ座標は、２－６＝－４
ｙ＝ａｘ²にＱ（－４、４）を代入する。
４＝16ａ
ａ＝１/４

大問５―Ⅱ（関数）

（１）　63.0％
答案では求める過程も記述する。
ｙ＝１/２ｘ²にｘ＝－２を代入すると、ｙ＝２
Ａ（－４、８）→Ｐ（－２、２）
右に２、下に６だから、傾きは－６/２＝－３
Ｂから右に２、下に－６移動して、切片は２－６＝－４
ｙ＝－３ｘ－４

（２）①　28.3％！

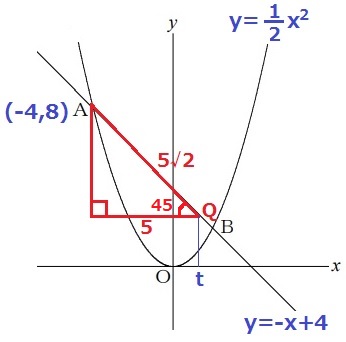
ｙ＝－ｘ＋４の傾きは－１→右下45°
ＡＱを斜辺とする直角二等辺三角形をつくる。
辺の比は１：１：√２、ＡＱ＝５√２ｃｍ→等辺は５ｃｍ
ｔ＝－４＋５＝１

②　0.0％!!!

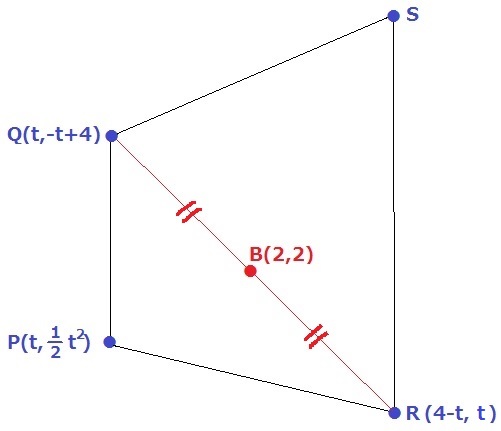
各座標をｔで表す。
ｙ＝１/２ｘ²とｙ＝－ｘ＋４にｘ＝ｔを代入。
Ｐ（ｔ、１/２ｔ²）Ｑ（ｔ、－ｔ＋４）

ＢはＱＲの中点。
ＱとＲのｘ座標を平均すると、Ｂのｘ座標の２になる。
ＱとＲのｘ座標の和は２×２＝４だから、Ｒのｘ座標は４－ｔ。
同様にＱとＲのｙ座標の和も４だから、Ｒのｙ座標は４－（－ｔ＋４）＝ｔ
Ｒ（４－ｔ、ｔ）

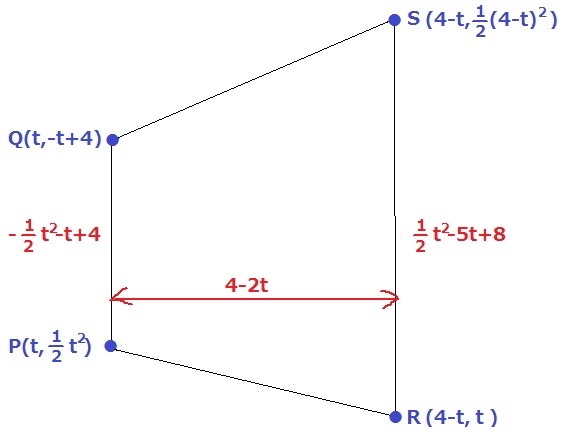
ｙ＝１/２ｘ²にｘ＝４－ｔを代入して、Ｓのｙ座標をｔで表す。
Ｓ（４－ｔ、１/２（４－ｔ）²）

非常に面倒であるが(´･_･`)、台形ＰＱＳＲの上底と下底、高さをｔで表す。
上底ＱＰ＝－ｔ＋４－１/２ｔ²＝－１/２ｔ²－ｔ＋４
下底ＳＲ＝１/２（４－ｔ）²－ｔ＝１/２ｔ²－５ｔ＋８
高さ＝４－ｔ－ｔ＝４－２ｔ

台形の面積で等式を立てる。
１/２（－１/２ｔ²－ｔ＋４＋１/２ｔ²－５ｔ＋８）（４－２ｔ）＝30
１/２（－６ｔ＋12）（４－２ｔ）＝30

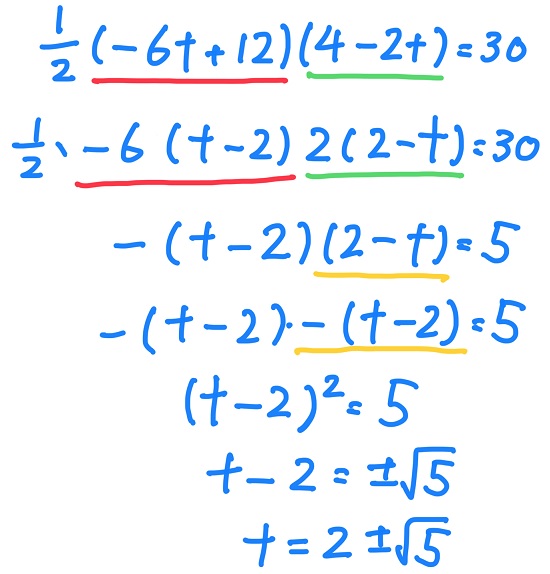
（－６ｔ＋12）＝－６（ｔ－２）、（４－２ｔ）＝２（２－ｔ）にして、
左辺の１/２と２を除外、両辺を÷６すると－（ｔ－２）（２－ｔ）＝５になる。
（２－ｔ）にマイナスをかけると－（ｔ－２）。
マイナス同士を相殺、（ｔ－２）²＝５の形にもっていけば解の公式を省くことができる。
－４＜ｔ＜２より、ｔ＝２－√５