2020年度　鹿児島県公立高校入試問題過去問【数学】解説

平均42.3点（前年比；＋4.1点、普通科に限ると平均49.8点）

問題はコチラ→ＰＤＦファイル

大問１（小問集合）－74.4％

（１）①　95.4％
８÷４＋6
＝２＋６＝８

②　91.3％
１/２＋９/10×５/３
＝１/２＋３/２=２

③　85.7％
２√３＋√27－３/√３
＝２√３＋３√３－√３
＝４√３

④　59.4％
ａとｂの積が負→ａとｂの一方が正、他方が負。
アが外れる。
ｃを含むと正→負×負＝正なので、ｃは負。
エ

⑤　44.9％
立面図が正面、平面図が真上からみた図。
真上の矢印がわかりにくい。
矢印の指している部分が三角柱の後ろ側にあるので、
そちらを下にして見ると逆三角形になるのでア。

（２）　67.9％
反比例；ｙ＝ａ/ｘ
ａ＝２×（－３）＝－６
ｙ＝－６/ｘ

（３）　60.7％
整数は根号のなかが平方数。
√４＜√７→√７は２より大きい。
√31＜√36→√31は６より小さい。
この範囲にある整数は、３・４・５。

（４）　82.9％
１～６の周期。
100÷６＝16…４
余り４→４

（５）　82.0％
独特臭はするが…問題はいたってシンプル。
1.5倍したとき、最も標高の高い宮之浦岳（1936ｍ）を超える→□×３/２＞1936
□＝1936×２/３＝1290.6…ｍ
これよりも高いものを選べばいい。

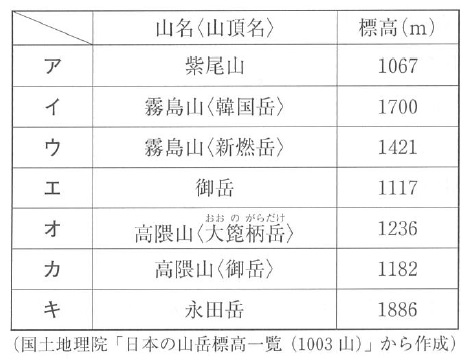
イ・ウ・キ
*韓国岳は〔カンコクダケ〕ではなく、〔カラクニダケ〕と読むそうです。
名称の由来は朝鮮半島を眺められるほどの山だからという話がありますが、
実際は登ってもまったく見れないという(;￣Д￣)
他に、大陸からやってきた渡来人に縁をもつ説もありました。

大問２（小問集合２）－51.4％

（１）　64.2％

∠ＡＢＣ＝（180－42）÷２＝69°
Ｂを通る平行線をひき、錯角47°を上にあげる。
∠ＡＢＤ＝69－47＝22°
これをさらに錯角であげ、ｘ＝22°

（２）　35.6％
条件の把握は正確に！
200ポイントとなる場合を考える。
①硬貨１枚だけが表、当たりをひくと１×200＝200ポイント
２枚の硬貨の結果は２²＝４通り
そのうち、１枚が表になるパターンは２通りなので、確率は２/４＝１/２
２本のくじから１本の当たりをひく確率は１/２
１/２×１/２＝１/４
②硬貨が２枚とも表、外れをひくと２×100＝200ポイント
１/４×１/２＝１/８
したがって、１/４＋１/８＝３/８

（３）　43.8％
比例式。
ｘ：（４ｘ－１）＝１：ｘ
外項と内項の積より、
ｘ²＝４ｘ－１
ｘ²－４ｘ＋１＝０
因数分解ができないので解の公式。
ｘの係数が偶数だから、ｂ＝２ｂ’が使える。
ｘ＝２±√３

（４）　39.9％

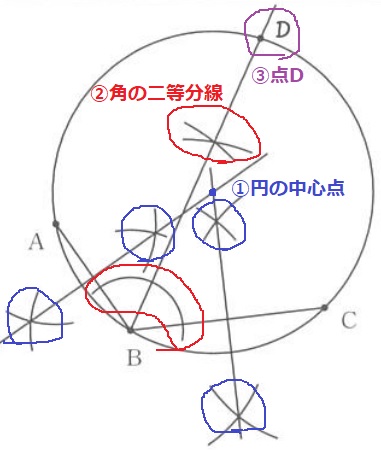
①ＡＢＣを通る円の作図。ＡＢ、ＢＣの垂直二等分線→交点が円の中心
②∠ＡＢＣの二等分線
③弧ＡＣとの交点がＤとなる。

（５）　71.1％
連立方程式。過程も記述する。
ｘ＋ｙ＝50　…①
ｘ/２＋ｙ/３＝23　…②
分母を払うため、②を６倍すると、
３ｘ＋２ｙ＝138　…③

③－①×２
３ｘ＋２ｙ＝138
－)２ｘ＋２ｙ＝100
ｘ　　　　＝38
①に代入。ｙ＝50－38＝12
したがって、Ａは38本、Ｂは12本。

大問３（データの活用）－42.8％

（１）　28.6％！
Ｂ組とＣ組の平均点＝Ｂ組とＣ組の総和÷50人
総和は、20×54＋30×65＝3030点
3030点÷50人＝60.6点

（２）①　77.6％
パっと見てヒストグラムの面積が広い、③が30人いるＣ。
①と②を比べると、②は左に偏っているので、平均の低いＢが②と推測する。
中央値で確かめる。20人のメジアンは10番目と11番目の平均。
②の10番目は40～50、11番目は50～60の階級に含まれるので、
Ｄの61.5ではなく、Ｂの49.0が中央値として適当といえる。
まとめると、Ｂが②、Ｃが③、Ｄが①。
ア…③　イ…①

②　39.3％
階級値に直して、ひたすら計算(´Д｀)
35×４＋45×６＋55×５＋65×６＋75×６＋85×３
＝140＋270＋275＋390＋450＝1780
1780÷30＝59.33…→59.3点

（３）　13.9％！
10番目をＸ、11番目をＹとする。
20人のメジアンはＸとＹの平均値で49点。
ＸとＹの差が４点ということは、平均から２点ずつ離れ、
10番目のＸは47点、11番目のＹは51点となる。

21人の中央値は11番目。
欠席者は76点なので、11番目はＹの51点。

大問４（平面図形）－20.1％

今年は観覧車のゴンドラでした。
（１）ア…75.2％、イ…9.0％!!
中心角360°を36等分する。
∠ＸＯＹ＝360÷36＝10°（ア）

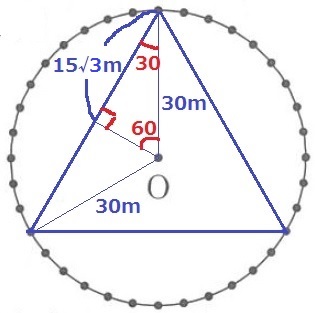
１周15分→５分間で120°（３分の１）回転する。
30°－60°－90°の直角三角形から、30×√３/２×２＝30√３ｍ（イ）

（２）　15.0％！
円周角定理の証明。

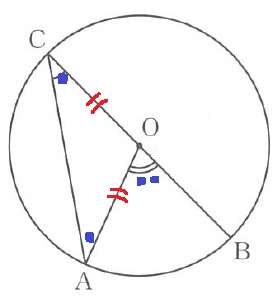
半径から△ＯＡＣは二等辺。
∠ＯＡＣ＝∠ＯＣＡ＝●とする。
△ＯＡＣの外角定理で、∠ＡＯＢ＝●●となり、
∠ＡＣＢ＝１/２∠ＡＯＢが成り立つ。

（３）①　7.2％!!

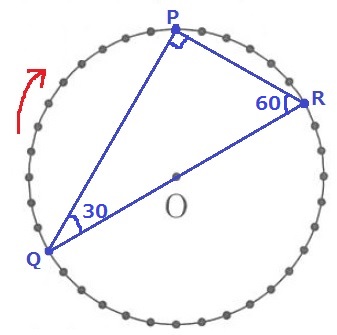
ゴンドラの位置は正確に！ここで失敗するとどうしようもない。
（１）イより、∠ＰＱＲ＝30°
直径に対する円周角は直角→∠ＱＰＲ＝90°
△ＰＱＲの内角は30°－60°ｰ90°

観覧車は時計回りにまわるとして、ＱＲ//Ｐ’Ｒ’となるには何度回転させればよいだろう？　

とりあえず、平行になるよう適当に描いてみる。
ポイントは直径ＱＲの中点が中心Ｏであり、Ｑ’Ｒ’の中点もＯであること！
同位角で∠Ｑ’ＯＲ＝60°
△ＯＰＲは半径より二等辺。∠ＯＲＰ＝∠ＯＰＲ＝60°
残りの角度である∠ＰＯＲ＝60°で△ＰＯＲは正三角形。
∠Ｑ’ＯＲ＝∠ＰＯＲ＝60°ということは、Ｑ’とＰは一致する！

Ｑ’の反対側がＲ’で、Ｐ’はＲ’から右に６個目の点。
回転先は赤いＰ’Ｑ’Ｒ’になる。

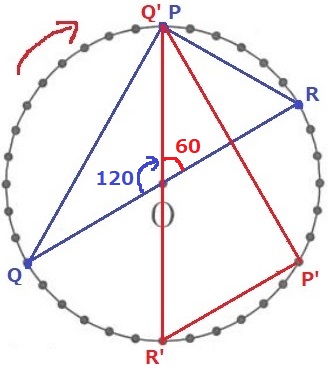
回転の角度は∠ＱＯＱ’に着目して120°
観覧車は15分で１周360°まわるので、120°は５分（ｔ＝５）

②　2.1％!!

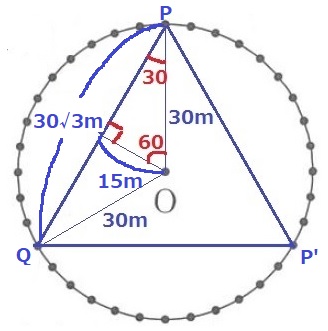
△ＰＱＰ’は正三角形になる。
すでに（１）イで見た形である。△ＰＱＯの面積を３倍すればいい。
30√３×15÷２×３＝675√３ｍ²

大問５（関数）－18.9％

（１）　69.8％
ｙ＝１/２ｘ²にｘ＝２を代入。
ｙ＝１/２×２²＝２
Ｑ（２、２）

（２）　18.8％！
Ｐ・Ｑ・Ｒ、すべてｘ座標はｔ。
ＱＲの距離は、
１/２ｔ²－（－ｔ²）＝３/２ｔ²

３/２ｔ²＝27/８　←27も８も立法数
ｔ＞０より、ｔ＝３/２

（３）①　7.7％!!

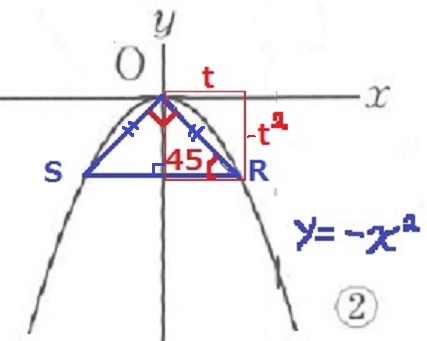
△ＯＳＲが直角二等辺三角形→∠ＯＲＳ＝45°
ＯＲは赤枠の正方形の対角線→ＯＲの傾きはー１→ｙ＝－ｘ
Ｒはｙ＝－ｘ²とｙ＝－ｘの交点。
－ｘ²＝－ｘ
ｘ²－ｘ＝ｘ（ｘ－１）＝０
ｘ＞０から、ｘ＝１
Ｒ（１、－１）

②　1.0%!!!
過程も記述する。
手法は回転体の問題でよくあるパターンなので処理能力がものをいう。
以下、公式解答を参考。

ｔ＝１より、Ｑ（１、１/２）Ｒ（１、－１）
ＱＲ＝３/２

Ｔ座標は、ｙ＝１/２ｘ²とｙ＝－ｘの交点。
１/２ｘ²＝－ｘ　←両辺を２倍して移項
ｘ²＋２ｘ＝ｘ（ｘ＋２）＝０
ｘ＝０、－２
Ｔのｘ座標は負なので、Ｔ（－２、２）

三平方でＴＲの長さを求める。
ｙ＝－ｘの傾きは－１→45度線→１：１：√２でＴＲ＝３√２

ＱからＴＲに向けて垂線、その足をＨとする。
△ＱＨＲは直角二等辺なので、同様に１：１：√２でＱＨ＝３/２√２
よって、（３/２√２）²×π×３√２×１/３＝９√２/８