平均61.7点（前年比；＋4.1点）
問題はコチラ→ＰＤＦファイル
大問１（小問集合）－73.8％
（１） 84.9％
－６2×１/９－４
＝－36×１/９－４
＝－８
（２） 68.1％
２ａ＋ｂ－（５ａ＋ｂ）/３
＝｛２ａ×３＋３ｂ－（５ａ＋ｂ）｝/３
＝（６ａ＋３ｂ－５ａ－ｂ）/３
＝（ａ＋２ｂ）/３
（３） 83.4％
（√７－１）（√７＋６）
＝７＋６√７－√７－６
＝１＋５√７
（４） 93.5％
２ｘ－８＝－ｘ＋４
３ｘ＝12
ｘ＝４
（５） 86.2％
５ｘ＋７ｙ＝９ …①
３ｘ＋４ｙ＝６ …②
①×３－②×５をすると、ｙ＝－３
②に代入、３ｘ＋４×（－３）＝６
ｘ＝６
ｘ＝６、ｙ＝－３
（６） 60.4％
（ｘ－８）２＝１
ｘ－８＝±１
ｘ＝８±１＝７、９
（７） 89.2％
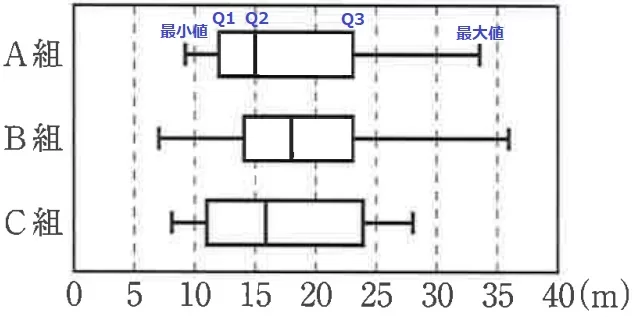
ア：Ｃの最大値は30ｍを超えない。×
イ：最大値が最も大きいＢ組にいる。×
ウ：15ｍはいずれも範囲内だから、15ｍの生徒がいる可能性はある。×
範囲（レンジ）＝最大値－最小値
エ：四分位範囲＝第３四分位数（Q3）－第１四分位数（Q1）
箱の長さが最も短いのはＢ組。〇
エ
（８） 52.1％
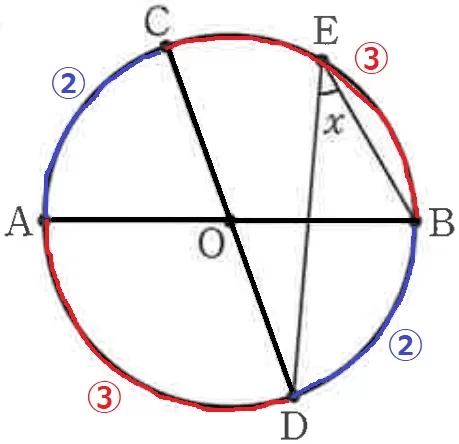
弧ＡＣ＝②とすると、弧ＡＢ＝⑤
弧ＣＢ＝⑤－②＝③
ＡＢとＣＤは中心Ｏを通る直径→対称性からＢＤ＝②、ＡＤ＝③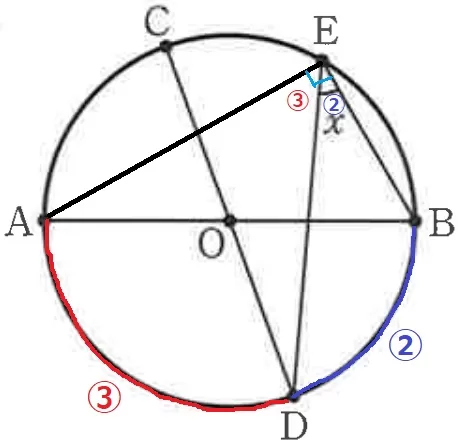
ＢＥに補助線。
半円の弧に対する円周角より、∠ＡＥＢ＝90°
円周角の大きさは弧の長さに比例するので、ｘ＝90×②/⑤＝36°
あ…３、い…６
（９） 46.2％
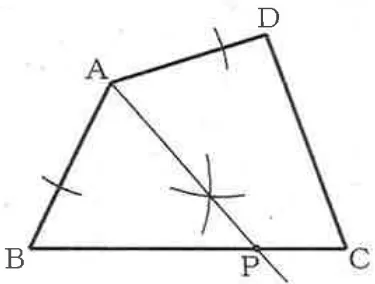
『ＰはＡＢとＡＤから等距離にある』→∠ＢＡＤの二等分線。
ＢＣとの交点がＰとなる。
*誤答はＡＢとＡＤの垂直二等分線をひき、その交点をＰとするものが多かった。
大問２（式の証明）－42.5％
（１） 61.1％
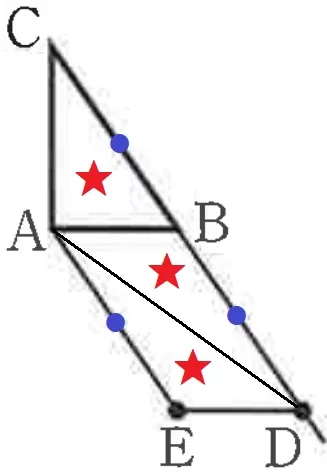
仮定よりＣＢ＝ＢＤ、平行四辺形の対辺は等しいからＢＤ＝ＡＥ
対角線ＡＤで平行四辺形を分けると、高さと底辺共通から★が等積。
四角形ＡＥＤＣの面積は△ＡＢＣの３倍。
う…３
（２） 23.9％！
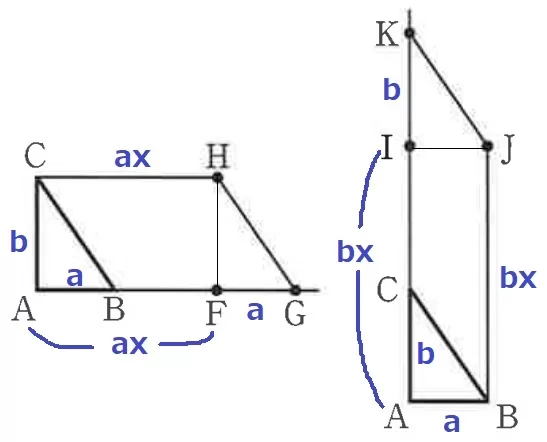
ＡＦ＝ａｘ、ＦＧ＝ＡＢ＝ａ
四角形ＡＦＨＣは長方形→ＣＨ＝ＡＦ＝ａｘ
四角形ＡＧＨＣの面積は、（ａｘ＋ａｘ＋ａ）×ｂ÷２
＝１/２ｂ（２ａｘ＋ａ）
＝１/２ａｂ（２ｘ＋１） …①
同様に四角形ＡＢＪＫの面積は、（ｂｘ＋ｂｘ＋ｂ）×ａ÷２
＝１/２ａ（２ｂｘ＋ｂ）
＝１/２ａｂ（２ｘ＋１） …②
①、②より、四角形ＡＧＨＣと四角形ＡＢＪＫは等積である。
＠余談＠
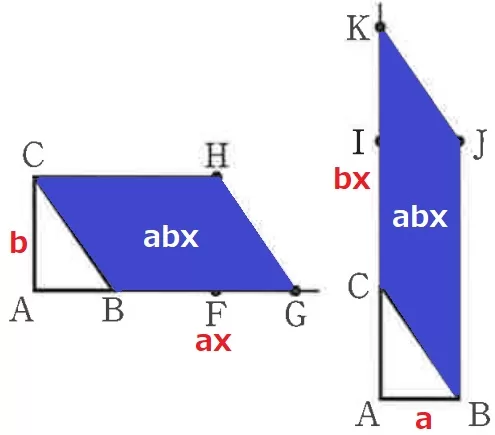
等積だけの指摘であれば、面積が増加する平行四辺形に絞るとわかりやすい。
平行四辺形の面積はａｘ×ｂ＝ｂｘ×ａ＝ａｂｘと同じである。
大問３（関数）－47.8％
（１） 69.8％
ｙ＝１/４ｘ2において、
ｘ＝０のとき、最小値ｙ＝０
ｘ＝－３のとき、最大値ｙ＝９/４
０≦ｂ≦９/４
①…エ、②…ク
（２） 64.6％
ｙ＝１/４ｘ2にｘ＝－６を代入→Ａ（－６、９）
同様にｘ＝２を代入して、Ｐ（２、１）
ＱはＰのｙ座標に４を足す→Ｑ（２、５）
Ａ（－６、９）→Ｑ（２、５）
右に８、下に４なので、傾きは－４/８＝－１/２
Ｑから左に２、上に１移動して、切片は５＋１＝６
ｙ＝－１/２ｘ＋６
③…ウ、④…ア
（３） 8.9％!!（無答率45.4％）
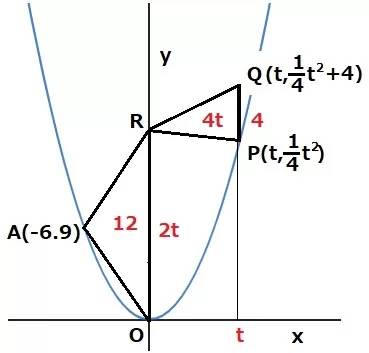
求めるべきＰのｘ座標をｔとする。
Ｐ（ｔ、１/４ｔ2）→Ｑ（ｔ、１/４ｔ2＋４）
△ＰＱＲの面積…４ｔ（÷２を省略しています）
△ＡＯＲの面積は４ｔ×３＝12ｔ、ＲＯ＝12ｔ÷６＝２ｔ
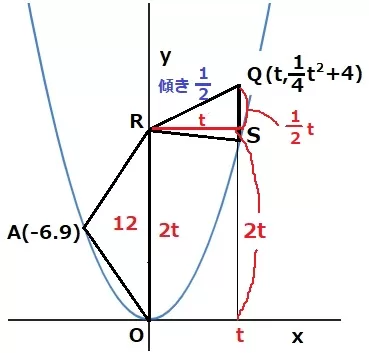
Ｒから右へ垂線をひき、足をＳとする。
ＱＲの傾きは１/２→Ｒから右にｔ、上に１/２ｔ移動してＱだから、ＱＳ＝１/２ｔ
Ｑのｙ座標は、２ｔ＋１/２ｔ＝５/２ｔ
Ｑのｙ座標で方程式を立てると、
１/４ｔ2＋４＝５/２ｔ ←４倍
ｔ2－10ｔ＋16
＝（ｔ－２）（ｔ－８）＝０
ｔ＞３だから、ｔ＝８
＠余談＠
答えから各座標を調べると、ＰとＳは一致します。
大問４（平面図形）－43.1％
（１） 73.2％
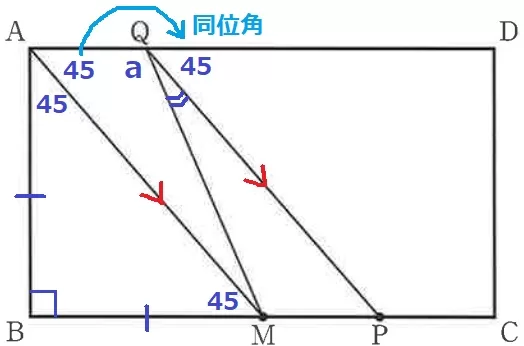
ＡＢ＝ＢＭ、∠ＡＢＭ＝90°より、△ＡＢＭは直角二等辺三角形。
∠ＢＡＭ＝∠ＭＡＱ＝45°
ＡＭ//ＱＰの同位角で、∠ＰＱＤ＝ａ
∠ＭＱＰ＝180－（45＋ａ）＝135－ａ
イ
（２）① 50.1％
△ＢＭＲ∽△ＤＱＴの証明。
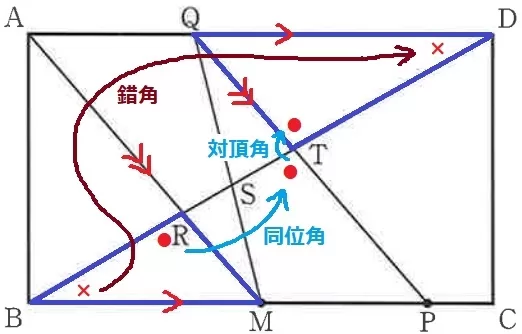
ＢＭ//ＱＤの錯角より、∠ＭＢＲ＝∠ＱＤＴ
ＡＭ//ＱＰの同位角→対頂角とつなげて、∠ＢＲＭ＝∠ＤＴＱ
２角が等しいから∽。
② 6.1％!!（無答率22.4％）
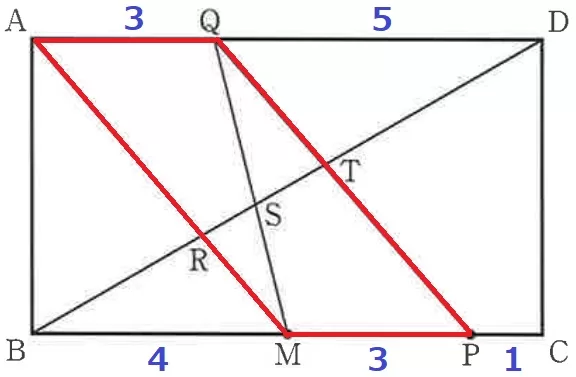
ＭＰ：ＰＣ＝３：１
MはＢＣの中点だから、ＢＭ＝４
平行四角形ＡＭＰＱの対辺からＡＱ＝３→ＱＤ＝５
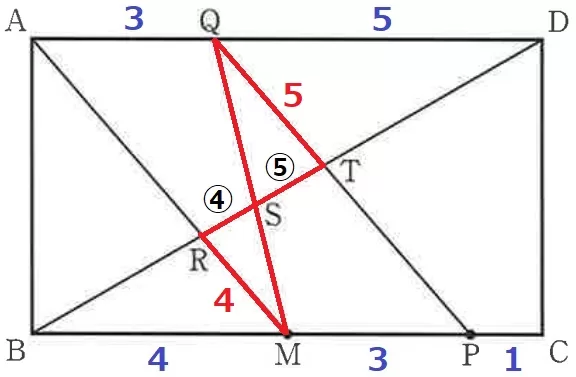
先ほどの△ＢＭＲ∽△ＤＱＴから、ＲＭ：ＴＱ＝４：５
△ＳＲＭ∽△ＳＴＱより、ＲＳ：ＳＴ＝④：⑤
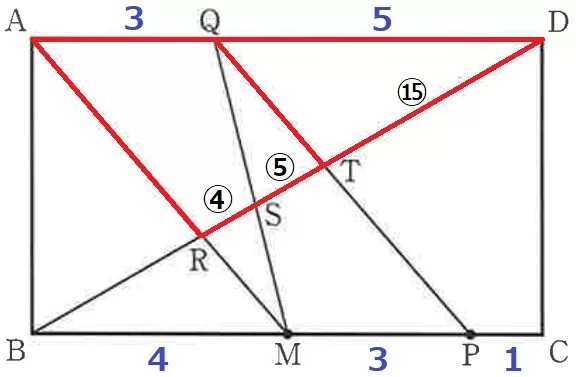
△ＡＲＤ∽△ＱＴＤより、ＲＤ＝⑨×８/３＝㉔
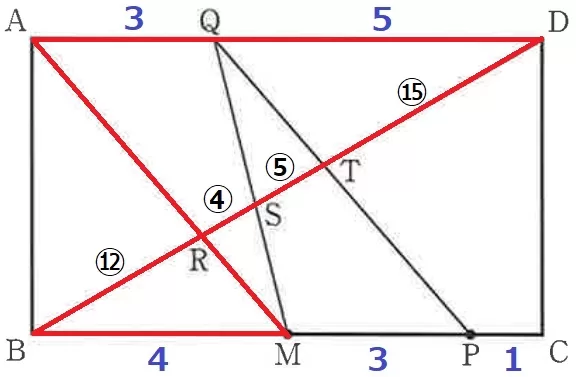
△ＡＲＤ∽△ＭＢＲより、ＢＤ＝㉔×12/８＝㊱
したがって、ＳＴ：ＢＤ＝５：36
え…５、お…３、か…６
大問５（空間図形）－28.0％
（１） 33.3％
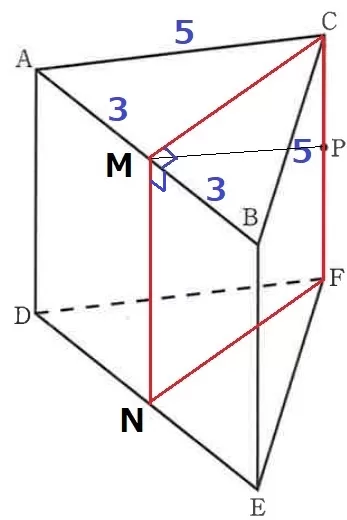
△ＡＢＣは二等辺三角形。
Ｍは底辺ＡＢの中点→ＡＢ⊥ＣＭ
Ｍの真下をＮとすると、ＢＭ⊥面ＭＮＦＣ
Ｐは面ＭＮＦＣ上の点だから、∠ＢＭＰ＝90°
き…９、く…０
（面ＭＮＦＣ上の点であれば、たとえば∠ＢＭＦも90°である）
（２） 22.8％！（無答率23.2％）
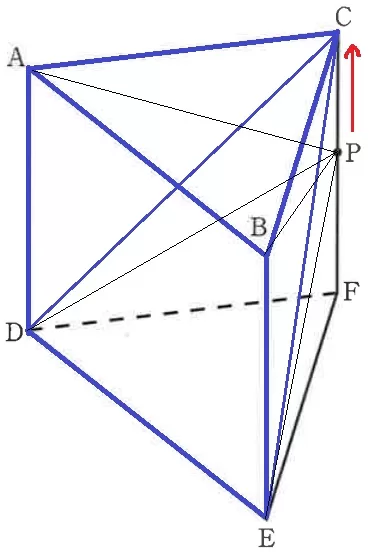
ＣＦ//面ＡＤＥＢより、Ｐ―ＡＤＥＢをＣ―ＡＤＥＢに等積変形する。
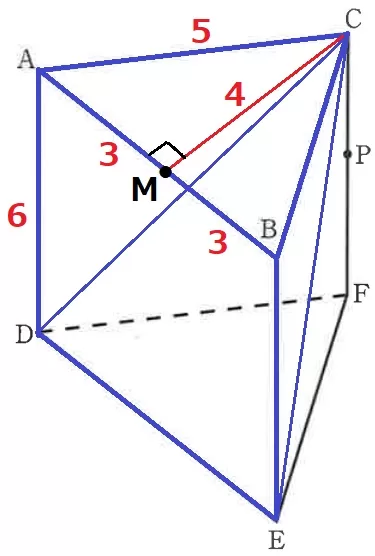
△ＡＭＣは３：４：５の直角三角形→ＣＭ＝４ｃｍ
Ｃ―ＡＤＥＢの体積は、底面ＡＤＥＢ×高さＣＭ÷３
＝６×６×４÷３＝48ｃｍ3
け…４、こ…８
易化です。（とくに図形分野）
大問１
計算は全部とる。
（６）いきなり展開しない。
（７）箱ひげ図は都立で初登場したが、設問は平易であった。
37人の中央値は19番目、第１四分位数は下から10番目、第３四分位数は上から10番目である。
（８）対頂角のように弧の長さを移す。
（９）作図もよくある形で取りやすい。
大問２
（２）ｘさえ図示できれば、台形の面積を文字で表すのみ。
立式しやすいかった。
大問３
（３）流れは例年通り。求めたいＰのｘ座標を文字に置き換え、各座標を文字で表す。
三角形の面積比からＲ座標がわかる。傾き１/２を使って、ＰではなくＱのｙ座標で方程式を立てる。
大問４
（２）①比較的見えやすい証明であった。
②構造が連比なので比の合成で良い。前問の合同を使うと先の解説のようになる。
大問５
（１）辺と面の関係性（垂直）を把握する。
（２）ラス問も見えやすかった。
底面はＡＤＥＢ、立体の高さは二等辺の高さ。分割も控除も不要であった。
＠2024年度・都立解説＠
数学(分割後期) 社会…準備中 理科…平均66.8点 英語…平均66.9点
公立高校入試解説ページに戻る
コメント