2019年度　長崎県公立高校入試Ａ問題【数学】解説

平均55.8点（前年比；＋2.3点）
問題はコチラ→ＰＤＦファイル
Ｂ問題の解説はこちら。

大問１（小問集合１）

（１）
８＋（－２）×３
＝８－６＝２

（２）
３/４－１/３＝５/12

（３）
√12－４√３
＝２√３－４√３＝－２√３

（４）
３（ｘ＋ｙ）－（２ｘ－ｙ）
＝３ｘ＋３ｙ－２ｘ＋ｙ
＝ｘ＋４ｙ
＝５＋４×（－１）＝１

（５）
①…ｙ＝100－ｘ
ｙ＝－ｘ＋100なので１次関数。
②…ｙ＝πｘ²
③…ｙ＝４ｘ（比例）
④…ｙ＝６/ｘ（反比例）
反比例はｘｙの値が一定になる。
したがって、④。

（６）
連立。
ｘ＝１、ｙ＝－１

（７）
ｘ²＋６ｘ＋８
＝（ｘ＋４）（ｘ＋２）

（８）
ｘ²＋５ｘ＋２＝０
因数分解できないので解の公式。
ｘ＝（－５±√17）/２

（９）

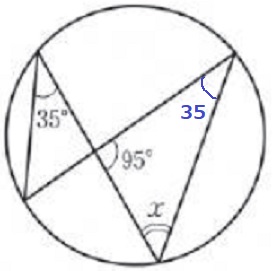
円周角定理で35°を右側へ移動する。
ｘ＝180－（95＋35）＝50°

（10）
角の二等分線の作図。
①Ｏから適当な弧を引く。
②ＯＡ，ＯＢの交点からそれぞれ適当な弧を描く。
③うえの交点とＯを結ぶ。

大問２（小問集合２）

（１）①
取り出し方は箱Ａから４通り、箱Ｂから４通りなので、
４×４＝16通り

②
引き分けは（陽平、明子）＝（１、１）（４、４）のとき。
２/16＝１/８

③
【全体－引き分け＝勝敗がつく】
１－１/８＝７/８
*ちなみに、陽平が勝つ確率は８/16＝１/２
明子が勝つ確率は６/16＝３/８になる。

（２）①
10人の中央値⇒５番目と６番目の平均値。
５番目は４点、６番は５点なので、中央値は4.5点。

②
４点は２人なので、２÷10＝0.2
相対度数は分数ではなく、小数であらわす。

③
範囲（レンジ）＝最大値－最小値
Ａ…範囲が広い。平均値4.5点。
Ｂ…範囲が狭い。４と５の間を対称の軸とすると左右対称→平均値4.5点
平均値はＡとＢで同じだが、範囲はＡの方がＢより大きい。
*高校数学ではデータのバラつき度合を分散で求めます。

（３）
抽出した120個のうち、アルミは75個だった。
全体：アルミ＝120：75＝８：５
4800×５/８＝3000個

大問３（関数）

（１）
ｙ＝ｘ²にｘ＝２を放り込む。
ｙ＝２²＝４

（２）
ｘ＝－１を放り込んで、Ａ（－１、１）
Ａ（－１、１）⇒Ｂ（２、４）
右に３、上に３なので、傾きａ＝１。
Ａ（－１、１）から右１上１がｙ軸との交点。切片ｂ＝２。
ｙ＝ｘ＋２

（３）
等積変形でＡとＢをｘ座標に降下させると、
底辺が３、高さ２の三角形となる。
３×２÷２＝３

（４）
ＯＢをひいて四角形ＯＡＢＰを分割。
前問で△ＯＡＢの面積が３だったので、
△ＯＢＰ＝11/２－３＝５/２

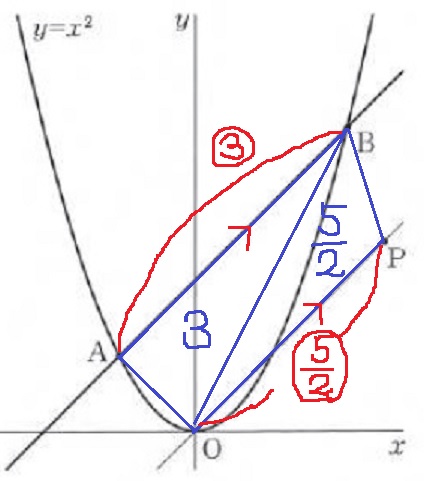
平行線なので、鹿右傾ＯＡＢＰは台形。
△ＯＡＢ：△ＯＢＰ＝３（上底）：５/２（下底）
平行線は高さが等しいから、底辺の比が面積比になる。
ＡＢ：ＯＰ＝３：５/２

２本の平行線は傾きが１。
つまり、ｘ軸との間の角は45°になる。

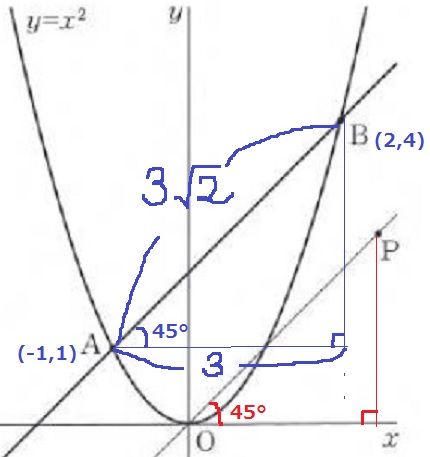
うえのように補助線をいれると、45°－45°－90°の直角二等辺三角形があらわれる。
ＡとＢのｘ座標の距離が３なので、１：１：√２から、ＡＢ＝３√２
ＯＰ＝３√２×（5/2）/ ３＝５√２/２

同様に、１：１：√２より、５√２/２×１/√２＝５/２
Ｐのｘ座標は５/２。

大問４（空間図形）

（１）
【ねじれの位置】⇒平行でもない、かつ延長しても交わらない。
ＤＦとＥＦとＣＦで３本。

（２）
４×４÷２×８＝64ｃｍ³

（３）
錘の体積は柱の３分の１。

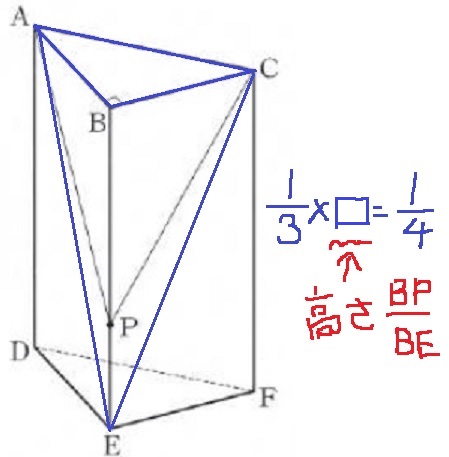
三角錐Ｅ－ＡＢＣが三角柱の体積の１/３倍にあたる。
ここから高さを調節する。
最終的に三角柱の体積の１/４倍になるので、高さを□とおくと、
１/３×□＝１/４
□＝１/４÷１/３＝３/４
ＢＥを３/４倍すればＢＰになる。
ＢＰ＝８×３/４＝６ｃｍ

（４）
水面の高さがは５ｃｍ。
水のあるところの体積：水がないところの体積＝⑤：③
容器を傾けても体積比は変化しない。

四角形ＡＤＦＣを底面とするので、高さを△ＡＢＣ方向から見る。

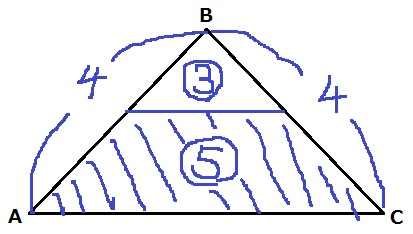
柱なので奥行きが等しいから、体積比は底面積の比と同じ。
水あり：水なし＝⑤：③

面積比は辺の２乗。
２乗して③となる→□√３
２乗して⑧となる→□√８＝□２√２
ＡＢ：ＧＢ＝２√２：√３

Ｂから垂線をおろし、交点をＩ・Ｈとする。
△ＢＨＣは直角二等辺三角形だから、１：１：√２でＢＨ＝４×１/√２＝２√２ｃｍ

△ＢＧＩ∽△ＢＡＨより、ＢＨ：ＩＨ＝２√２：２√２－√３
２√２×（２√２－√３）/２√２＝２√２－√３ｃｍ

大問５（平面図形）

（１）
半径より、ＯＡ＝ＯＢ。
△ＯＡＢは二等辺三角形なので、（180－120）÷２＝30°

（２）①

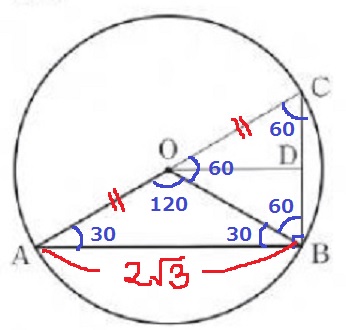
角度を調べていくと、△ＡＢＣは30°－60°－90°の直角三角形。
１：２：√３より、ＡＣ＝２√３×２/√３＝４ｃｍ

②
△ＣＯＤ∽△ＣＡＢ
ＡＢ：ＯＤ＝ＡＣ：ＯＣ＝２：１
ＯＤ＝２√３×１/２＝√３ｃｍ

③ア
△ＯＤＥ∽△ＢＡＥの証明。
ＯＤ//ＡＢなので、対頂角やら錯角やらで２角が等しい点を指摘する。

イ
前問の∽を利用する。
△ＯＤＥ∽△ＢＡＥ
ＯＥ：ＢＥ＝ＯＤ：ＢＡ＝１：２

△ＢＱＥ∽ＢＤＯ
ＤＱ：ＱＢ＝ＯＥ：ＥＢ＝１：２
ＤはＢＣの中点。
連比を組んで、ＣＤ：ＤＱ：ＱＢ＝３：１：２

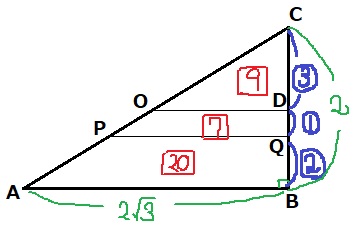
面積比は辺の２乗。
△ＣＯＤ＝③×③＝□９
四角形ＯＰＱＤ＝④×④－□９＝□７
四角形ＰＡＢＱ＝⑥×⑥－□16＝□20

△ＡＢＣは１：２：√３の直角三角形。
ＢＣ＝２√３×１/√３＝２ｃｍ
四角形ＯＰＤＱ＝２√３×２÷２×７/36＝７√３/18ｃｍ²

大問６（整数）

（１）
28の約数。
１、２、４、７、14、28

（２）
３√３＝√27、２√６＝√24
√24＜√26＜√27
２√２＜√26＜３√３

（３）
ａ²＋ｂ²＝10²を満たす、自然数ａ、ｂの組合せを答える。
ａとｂは１以上９以下なので、
１～９の平方数１・４・９・16・25・36・49・64・81のなかから、
我が100になる組合せを調べると、36＋64＝100
ア：６、イ：８

＠別解＠
３：４：５でピタゴラス数となるので、
２倍して６：８：10からａ＝６、ｂ＝８といける。

（４）
【３以上の奇数ａの平方数が、連続する２つの自然数ｂ、ｃの和と等しくなると、
ａ²＋ｂ²＝ｃ²が成り立つ】
41は奇数なので、ａ＝41が解答の１つ。
もう１つは連続するｂ・ｃのうちのいずれかが41。
（例題をみるとｃが奇数なので、ｃが41ではないかと推測しておく）

◆ａ＝41
連続する２つの自然数をｎ、ｎ＋１とおく。
41²＝ｎ＋（ｎ＋１）
２ｎ＝1680
ｎ＝840
（ａ、ｂ、ｃ）＝（41、840、841）

◆ｂかｃ＝41
例題ではｃが奇数なので、ｃに41を当てはめてみる。
ｂはｃの１つ前の数なので40。
ａ²＝40＋41＝81
ａ＝９
（ａ、ｂ、ｃ）＝（９、40、41）
（９、40、41）と（41、840、841）

（５）
整数の証明問題。
連続する３つの自然数はｎ、ｎ＋１、ｎ＋２となる。
これらをａ、ｂ、ｃにあてはめる。
ｎ²＋（ｎ＋１）²＝（ｎ＋２）²
ｎ²－２ｎ－３
＝（ｎ－３）（ｎ＋１）０
ｎは自然数なのでｎ＞０
ｎ＝３
ピタゴラスの定理（三平方の定理）ａ²＋ｂ²＝ｃ²において、
ａ、ｂ、ｃが連続する自然数でａ＝３だから、
連続する３つの自然数の組合せからなるピタゴラス数は（３、４、５）

＠ピタゴラス数＠
整数ｍ、ｎで、ａ＝ｍ²－ｎ²、ｂ＝２ｍｎ、ｃ＝ｍ²＋ｎ²とすると、
ａ²＋ｂ²＝ｃ²が成立する。

ｍ＝７、ｎ＝５
ａ＝７²－５²＝24
ｂ＝２・７・５＝70
ｃ＝7²＋５²＝74
24²＋70²＝576＋4900＝5476＝74²
この定理を使うとすべてのピタゴラス数を表せる。
公立高校入試解説ページに戻る