問題PDF
(1)
次の□にあてはまる数を求めなさい。

(2)
図において三角形ABCは正三角形です。
(あ)の角の大きさを求めなさい。
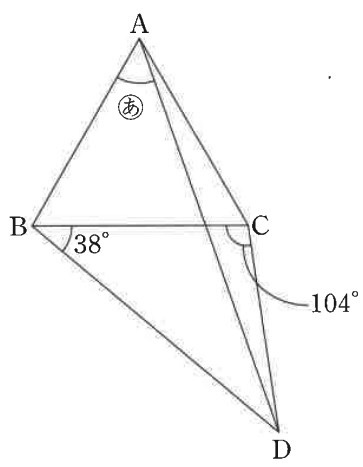
(3)
1からAまでのすべての整数を1回ずつかけ合わせた数を《A》と表します。
例えば、《3》=1×2×3=6です。
次のB、Cには、あてはまる整数はいろいろ考えられますが、
Bにあてはまる整数のうち、最も小さいものを答えなさい。
《2》×《3》×《4》×…×《10》×B=C×C×C
(4)
はじめ、容器A、Bに入っている水の量の比は9:7でした。
容器A、Bに水をそれぞれ16リットル、12リットル加えると、
容器A、Bの水の量の比は17:13になりました。
はじめ、容器Aに入っていた水の量は何リットルでしたか。
(5)
同じ長さの7本の矢印を横一列に並べます。

例1のように、となり合うどの2本の矢印の組も向き合ってないような
7本の矢印の並べ方は〔 ア 〕通りあります。
例2のように、となり合う2本の矢印の組のうち、
1組だけが向き合っているような7本の矢印の並べ方は〔 イ 〕通りあります。
〔 ア 〕、〔 イ 〕にあてはまる数を求めなさい。
@解説@
(1)

(2)
よくあるパターンなので想像はつきやすい。
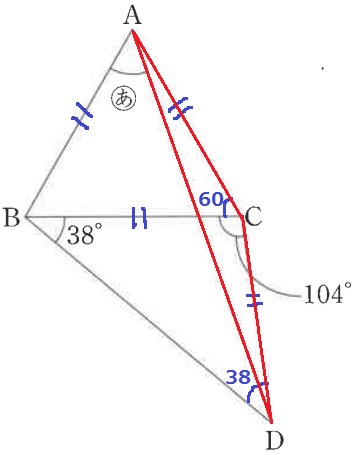
△BCDの内角から、∠CDB=180-(104+38)=38°
△BCDは2つの底角が等しく二等辺三角形。
AC=DCで△ACDも二等辺。
∠CAD=(180-60-104)÷2=8°
(あ)=60-8=52°
(3)
積が何か(C)の3乗になる。
→すべての種類の素因数が3の倍数個になる。

*実際の試験では、〔2が9個、3が8個、4が7個…〕と文字で書いて対処。
同じ数を3個セットで消していくと、3・3・4・6・6・7・9・9・10が残る。
さらに、素因数に分解して3個セットで消す。
3×3×(2×2)×(2×3)×(2×3)×7×(3×3)×(3×3)×(2×5)
残りは2が2つ、3が2つ、5が1つ、7が1つ。
積を何かの3乗にするには、2を1つ、3を1つ、5を2つ、7を2つ追加すればいい。
2×3×5×5×7×7=7350
(4)
消去算(ほぼ連立方程式)
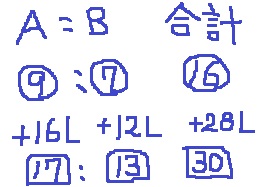
問題文の情報を整理する。
はじめはA:B=⑨:⑦
⑨+16L=□17
⑦+12L=□13
合計すると、⑯+28L=□30

それぞれの式をⅠ~Ⅲとする。
Ⅰ-Ⅱ:②+4L=□4 …Ⅳ
Ⅳ×8-Ⅲをして〇を消去すると、4L=□2となる。
□30=4L×30/2=60L
Ⅲの式から、⑯=60-28=32L
最後に⑯を⑨:⑦に按分して⑨を求める。
32L×9/16=18L
(5)
①7本の矢印すべてが左を向いていたとする。
②一番右側の矢印だけ右を向く。
③右側2本だけが右を向く。
④右側3本だけが右。
⑤右側4本だけが右…
とやっていくと、右側を向く矢印の本数は0~7本の8通り。
ア…8
同じ向きの矢印は、大きな矢印でつなげて考えてみる。
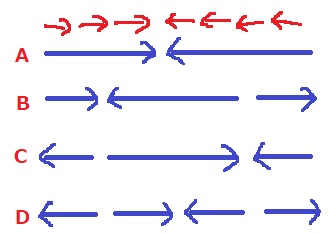
1組だけ向き合うパターンは、うえの4通り。
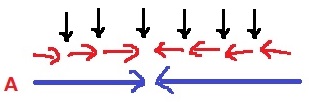
A:矢印を向き合わせるポイントを、あいだの6つから1つ選ぶ→6通り
B:あいだの6つから2つを選ぶ→6C2=15通り
C:Bと左右対称だから15通り
D:6つから3つを選ぶ→6C3=20通り
6+15+15+20=56通り
イ…56



コメント