2019年度　栄光学園中学過去問【理科】解説

問題ＰＤＦ
　栄一君の家の近くには、山をけずって道を通した切り通しがあります。切り通しの両側のがけには、土がくずれるのを防ぐために、図１のように「石積み」がされています。石は長方形に近い形で、石と石の間にはモルタル（コンクリート）がつめられていますが、ところどころ割れたり欠けたりしていて、石のすき間からいろいろな草が生えています。

　栄一君は、石積みに生えている植物の種類を調べてみました。
図１のような石積みがされている場所で、まず、石積みをはしから長さ２ｍごとに分けて、順に「区画１」「区画２」…と呼ぶことにしました。そして、石積みを「区画１」から順に観察して、それぞれの区画で見つけた植物の種類として生えている位置をすべて記録しました。
　「区画１」から「区画38」まで調べた結果、全部で22種類の植物が見つかりました。その中には、ススキ、ヤマグワ（クワ）、タンポポなどがありました。

　横軸に区画の番号、縦軸に「区画１」からその区画までの間に生えていた植物の種類の数をとってグラフをかくと、図２のようになりました。

問１
栄一君が調べた石積みに、植物はどのように生えていたでしょうか。
「区画１」から「区画８」までに生えている植物を表す図として適当なものを選びなさい。
図の中のアルファベットは、それぞれ異なる植物の種類を表します。

図３は、ススキの穂です。
図４は、ススキの花の１つ１つがよく見えるように広げたものです。

問２
図３のススキの穂には、種子が何個できると推定できますか。
最も適当なものを１つ選びなさい。１つの花から１つの種子ができるものとします。
ア：10個未満　イ：10個～100個　ウ：100個～1000個
エ：1000個～10000個　オ：10000個～100000個　カ：100000個以上

問３
切り通しのまわりには、ススキ、ヤマグワ、タンポポなどの石積みで見られたものと同じ植物が生えています。また、コナラなどのドングリがなる木も生えていますが、ドングリのなる木は、石積みには生えていません。図５は、栄一君がいろいろな季節に作った観察カードです。これを参考にして、石積みに生えるのに有利な植物の実の特徴を２つあげなさい。また、それぞれについて、有利になる理由を書きなさい。

図６は、図１の一部です。栄一君は、石積みは図７のような積み方が多いのかと思っていましたが、注意してみると、図６のような積み方をしている場所も多いことに気づきました。図８のような積み方の石積みを見かけることもあります。

いろいろな積み方があって面白いと思ったので、このことを先生に話してみると、
次のように教えてくれました。

「図７の積み方は、形や大きさはそろった石を用意できれば、規則的に積んでいけばよいので、積むのは簡単です。いっぽう、図８の積み方は、石と石の境の線が一直線にならないので、図７の積み方よりもじょうぶでくずれにくいのですが、形や大きさはそろっていない石をすき間なくきちんと積み上げることが難しいのです。」

問４
図６の積み方は、図７や図８とくらべてどのような点が良いか、説明しなさい。

栄一君は、図６を見ながら、石はどうやって積まれたのだろうと考えてみました。まず、図１の写真にうすい紙を重ねて、一部の石の輪かくをかき写し、図９のような図を作りました。

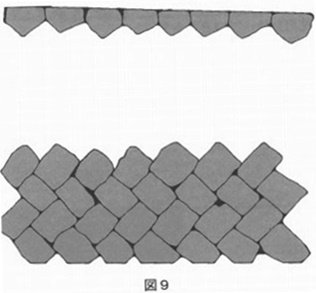
次に、あいている部分に、自分で積むつもりになって石積みの絵をかいてみました。すると、石の並べ方が規則的であること、大きさを考えて石が配置されていること、石を積む順序に決まりがあることなど、いろいろなことに気が付きました。

問５
解答用紙の「問５」の図の白い部分にうまく合うように、石積みの絵をかきなさい。
図10のように、石を１つずつかくようにすること。

石積みは、裏側にもくふうがされています。
図11は、先生が石積みの裏側のようすを教えるためにかいてくれた絵です。

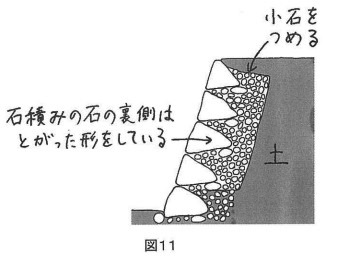
小石をつめた部分は、「積んだ石の重さを分散させて支える」「地しんなどのゆれを吸収して積んだ石を安定させる」などの役割を持っているそうです。そのためには、小石どうしのすき間が多くあって、簡単には動かない状態がよいそうです。

栄一君は、石の重さや体積を調べる実験をしてみました。

使ったもの
・でこぼこの石（図12の左）
・なめらかな石（図12の右）

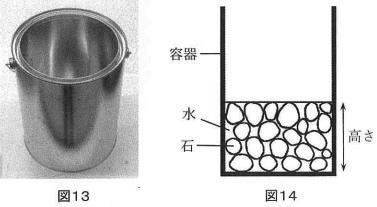
・円柱型の容器（図13）
中の底面積は210ｃｍ²

はかりかた
①でこぼこの石を容器の中に、適当な高さで平らになるように入れて、重さをはかりました。
②ちょうど石の高さと同じ高さになるように水を入れて、重さをはかりました。
　容器の中に石と水を入れた様子が図14です。
③高さをかえて①、②を８回行いました。
④でこぼこの石をなめらかな石にかえて、①～③を行いました。

測定結果
はかった数値から、それぞれの高さのときの石の重さと水の重さを計算しました。
でこぼこの石についての結果が表１です。

問６
表１を、横軸に高さ、縦軸に石や水の重さをとったグラフにします。
解答用紙の「問６」の図には、水の重さのグラフだけかいてあります。
石の重さのグラフをかきなさい。
水の重さのグラフと同じように、直線を引きなさい。

問７
横軸に高さ、縦軸に石や水の体積をとったグラフをかきます。
以下の（１）～（３）を、解答用紙の「問７」の図にかきなさい。

（１）
問６のグラフから、表１のそれぞれの高さのときに容器に入っていた水の体積がわかります。
高さに対する水の体積の関係を表す直線をかき、そばに（１）と書きなさい。
ただし、水１Ｌの重さを１ｋｇとします。

（２）
容器に水を入れずに水だけを入れた場合の、高さに対する水の体積の関係を表す直線をかき、
そばに（２）と書きなさい。

（３）
表１のそれぞれの高さのときに容器に入っていた石の体積を考えます。
高さに対する石の体積の関係を表す直線をかき、そばに（３）と書きなさい。

問８
でこぼこの石の、１ｃｍ³あたりの重さは何ｇですか。
四捨五入して小数第一位まで答えなさい。

問９
石を容器に入れたときの、石どうしのすき間について考えます。
（１）
容器の中にでこぼこの石を高さ10ｃｍまで入れたとき、
容器の底から10ｃｍまでの部分の体積のうち石の体積の割合は何％ですか。
四捨五入して整数で答えなさい。

（２）
なめらかな石を使った実験の結果を問６と同様のグラフにすると、図15のようになりました。
容器の中になめらかな石を高さ10ｃｍまで入れたとき、容器の底から10ｃｍまでの部分の体積のうち石の体積の割合は何％ですか。四捨五入して整数で答えなさい。

問10
容器に入れたときにすき間がより多くできるのは、
でこぼこの石となめらかな石のどちらだと考えられますか。

問11
石を容器に入れて水を入れたときの水の重さについて考えます。
容器の中に問10で答えた石を高さ10ｃｍまで入れ、石の高さと同じ高さになるまで水を入れると、
石と水を合わせた重さは石だけの重さの何倍になりますか。
四捨五入して小数第一位まで答えなさい。

雨がふると、雨水は地面にしみこんで土の中を通り、石積みの裏側に流れ出てきます。
その水はすき間を通り、最後には石積みの外へ出ます。
そのため、石積みには、水をぬくための穴が一定の面積ごとにあけられています。

問12
図16のように大きさと形の整ったブロックを積んだ石積みがあります。
このブロックの表面は長方形で、辺の長さは25ｃｍと40ｃｍです。
水をぬくための穴は、石積みの表面の面積何ｍ²ごとに１つずつあけられていますか。
小数第一位まで答えなさい。
なお、写真の外側も、写真と同じ規則で穴があけられているものとします。

もし、石積みから水が出なくなったら、小石のすき間に水がたまり、
その重さで石積みを外向きにおします。
そのために、石積みがくずれやすくなるかもしれません。

栄一君は穴からごみを取り出し、家に持って帰りました。

問２：エ
面白い設問だが目がいたくなる(;´Д｀)
ススキ10ｃｍの花を数えるとだいたい40個くらい？
１本平均30ｃｍとして、36本あるようにみえるので、
40×３×36＝4320個→エ

問３：
（実の特徴）－遠くに運ばれやすい。
（有利な理由）－種子が風にのったり、鳥に食べられることで、
高さのある石積みに種子を飛ばせる。

（実の特徴）－１粒の大きさが５ｍｍ以下と小さい。
（有利な理由）－石と石の隙間に種子が入り込み、
石積みでも植物が根を生やすことができる。
*観察カードをみて『石積みに生えるのに有利な植物の実の特徴』を推測する。
石積みは石の壁みたいなものなので、わざわざそこに生やすことのできる植物は限られてくる。

冠毛と白い毛→風の力で種子を飛ばす。
色がついた味のある実→鳥に食べてもらう。
ここから種子が遠くに移動できる点を指摘する。

もう１点は実のサイズに注目する。
ヤマグワは１房（ふさ）が約２ｃｍで、縦に８～９粒くらいみえるので、
１つの実の大きさは５ｍｍ以下になる。
石積みで植物が育つには、石の表面ではなく、石と石の隙間に種子が着地する必要がある。
答案を作成するときは、テーマである石積みに結びつけるように書きたい。

問４
石と石の境が一直線ではないので丈夫で崩れにくく、
石の形や大きさが似ているので簡単に積める。

問題文をパクッただけだが(;^ω^)
図７と図８の良いところ取りをした感じ。

問５
実際に石を積ませるなんて(*’ω’*)ｗ

サボの描写能力の限界です(;´Д｀)
互い違いに書けばいいが、上にいくにしたがってアウトラインの制約がきつい。。
ここであまり時間を使わないようにしたい。

問６

横軸は□のところ。縦軸の数値（石の重さ）から○をプロット。
必ず、近似値を直線でひくこと！（測定値には誤差を含むため）
原点０は通過しない。

問７

グラフ作成問題２。時間かかる( ﾉД`)
今度は縦軸が重さから体積に変わる。

重さは量りにかければ求められるが、不定形の石の体積は測れない。
そこで水を用いる。
容器の底面積は210ｃｍ²で、これに高さをかければ石＋水の体積（円柱）がでる。
水は１Ｌ＝１ｋｇとするので、水の体積は水の重さｋｇをそのままＬに変えればいい（１）。
石＋水の体積が（２）で、そこから水の体積（１）を引けば、石の体積（３）がでる。

（１）水１ｋｇ＝１Ｌなので、前問の水と同じ。
（２）（３）高さが2.4ｃｍの場合、
底面積が210ｃｍ²で高さ2.4ｃｍの円柱の体積なので、
210×2.4＝504ｃｍ³＝0.504Ｌ（２）
0.504Ｌ－0.28Ｌ＝0.224Ｌ（３）

以下、高さの順にプロットする縦軸。
（１）0.28Ｌ、0.39Ｌ、0.51Ｌ、0.60Ｌ、0.69Ｌ、0.82Ｌ、0.91Ｌ、1.00Ｌ
（２）0.504Ｌ、0.798Ｌ、1.05Ｌ、1.281Ｌ、1.512Ｌ、1.764Ｌ、2.016Ｌ、2.205Ｌ
（３）0.224Ｌ、0.408Ｌ、0.54Ｌ、0.681Ｌ、0.822Ｌ、0.944Ｌ、1.106Ｌ、1.205Ｌ
作業に時間を要するので、手際の良さが求められる。

問８：2.7ｇ
2.4ｃｍのとき、石の重さ＝620ｇ、石の体積＝224ｃｍ³
密度は、620ｇ÷224ｃｍ³＝2.76…ｇ/ｃｍ³

これを四捨五入して2.8かな？と思いきや、続きをやってみると、
3.8ｃｍのとき→1080÷408＝2.64…
5.0ｃｍのとき→1470÷540＝2.72…
6.1ｃｍのとき→1830÷681＝2.68…
7.2ｃｍのとき→2190÷822＝2.66…
8.4ｃｍのとき→2580÷944＝2.73…
9.6ｃｍのとき→2970÷1106＝2.68…
10.5ｃｍのとき→3270÷1205＝2.69…
↑電卓使いました。。
数値がバラバラになるのは、測定値に誤差はつきもののため。
（だから、高さを変えて８回も計測した）
数値を全体的にみて、小数第２位を四捨五入すると１ｃｍ³あたり2.7ｇとなる。
*有効数字が２桁なので、小数第３位は無視して計算していいのかも。。

問９（１）：55％
問７（３）のグラフから、高さと体積はだいたい比例関係。
ある高さにおいて、石の体積が占める割合は等しくなる。
10ｃｍに最も近い10.5ｃｍのとき、容器の体積は問７（２）より2205ｃｍ³。
石の体積は問７（３）より1205ｃｍ³。
1205÷2205×100＝54.64…→55％

（２）：62％
今度は、なめらかな石で測定する。
グラフしか与えられていないので、高さが10ｃｍのところをみると、
ちょうど石の重さが3500ｇ、水は800ｇになっている。

水の体積→800ｃｍ³
高さ10ｃｍまでの容器の体積→210ｃｍ²×10＝2100ｃｍ³
石の体積→2100－800＝1300ｃｍ³
1300÷2100×100＝61.9…62％

問10：でこぼこの石
前問で、同じ高さ10ｃｍで比較したとき、石が占める体積の割合は、
でこぼこ→55％、なめらか→62％
でこぼこの石の方が隙間が多く出やすい。

問11：1.3倍
これも問９（１）のように、高さ10.5ｃｍで考えるしかないような・・。
このとき、表１から石と水の重さは4.27ｋｇ、石の重さは3.27ｋｇなので、
4.27÷3.27＝1.30…→1.3倍

問12：2.4ｍ²

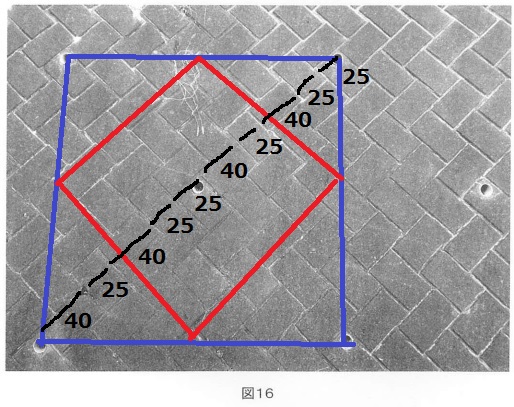
排水溝どうしの間（中点）を囲うと赤い正方形。
ブロックの辺に注目して、赤い正方形の１辺は、40＋25＋25＋40＋25＝155ｃｍ＝1.55ｍ
1.55×1.55＝2.4025→2.4ｍ²
正確な値はわからないので概算に頼るしかないが、
どこか見誤ると数字がズレる危機がある(;^ω^)

◆追記◆
ppppさんが細かく分析してくださいました。

図16を45度弱左に回転させ、方眼紙にのせた図です。
長方形の辺の比は５：８、排水溝は左上の頂点から右１下１で統一しています。
４つの排水溝を結ぶと１マスずれており、正確には正方形ではなく菱形でした。

規則正しい形に分割すると24個の長方形になるので、
25×40×24＝24000ｃｍ²＝2.4ｍ²

正方形とみなしても答えが一致するように作られていますが、
栄光は実験データなど細かい数字を取り扱う設問が毎年でてくるので、
どの程度まで正確に答えるべきか、くわしくは理科専任の先生に質問してください(;^ω^)
難関中学（理科）解説ページに戻る