2019年度　静岡県公立高校入試問題過去問【数学】解説

平均26.71点（50点満点）

問題はコチラ→ＰＤＦファイル

大問１（計算）

（１）①ア　97.3％
－12＋９÷３
＝－12＋３＝－９

イ　90.9％
（－５ａ）²×８aｂ÷10ａｂ
＝20ａ

ウ　91.8％
（ｘ＋ｙ）/３－（ｘ－３ｙ）/４
＝｛４（ｘ＋ｙ）－３（ｘ－３ｙ）｝/12
＝（４ｘ＋４ｙ－３ｘ＋９ｙ）/12
＝（ｘ＋13ｙ）/12

エ　88.9％
√６（√６－７）－√24
＝６－７√６－２√６
＝６－９√６

（２）　81.3％
式を整理してから代入。
ａｂ²－81ａ
＝ａ（ｂ²－81）
＝ａ（ｂ＋９）（ｂ－９）
＝１/７×28×10＝40

（３）　75.8％
（ｘ＋１）²＝３
ｘ＋１＝±√３
ｘ＝－１±√３

大問２（小問集合）

（１）　55.3％
円の中心点の作図。
Ａ・Ｂ・Ｃが同一の円周にくるので、直線ＡＢ、ＢＣ、ＣＡのうち、
いずれか２つの垂直二等分線が交わる点がＯとなる。

（２）　49.3％
単位換算に気をつけよう！
１ｇ＝0.001ｋｇ
30ｇ＝0.03ｋｇ
ｙ＝0.03ｘ　（ｙ＝３/100ｘ）
*誤答では、ｙ＝30ｘが多かったそうです。

（３）　73.4％
全体は６つから２つを選ぶ。
₆Ｃ₂＝15通り
３の倍数は12と15。
〔12と10・11・13・14〕
〔15と10・11・13・14〕
〔12と15〕計９通り
９/15＝３/５

＠別解＠
『少なくとも１個は３の倍数』だから、
〔全体－３の倍数以外〕でもＯＫ。
３の倍数以外⇒10・11・13・14から２つ選ぶ。
₄Ｃ₂＝６通り
１－６/15＝３/５

大問３（データの活用）

（１）　75.1％
１回以上の人数…32－８＝24人
24/32＝３/４＝75％

（２）　36.9％
ア：範囲（レンジ）＝最大値－最小値＝５－０＝５。×
イ：平均＝（0×8＋１×11＋2×7＋3×2＋4×3＋5×1）÷32＝48÷32＝1.5。○
ウ：最頻値（モード）は最も表れているデータ⇒１。×
エ：32人の中央値（メジアン）は、16番目と17番目の平均値⇒１。×
オ：最小値は０。○
イ・オ
*誤答ではアが多い。

大問４（方程式）

43.8％
過程も記述する。
問題文をぱっと見て、速さを使った方程式だと察せる。
線分図で情報整理！

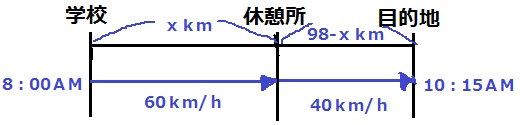
学校～休憩所をｘｋｍとおいて、休憩所～目的地が98－ｘｋｍ。
移動の合計時間は、10：15－8：00－0：20＝1：55＝115/60時間
時間で等式を作成する。

ｘ/60＋（98－ｘ）/40＝115/60　←120で通分
２ｘ＋294－３ｘ＝230
ｘ＝64ｋｍ
98－64＝34ｋｍ
学校～休憩所…64ｋｍ、休憩所～目的地…34ｋｍ

大問５（空間図形）

（１）　82.7％
△ＰＤＦは、底辺ＤＦ＝４ｃｍ、高さＡＤ＝９ｃｍ。
ＰがＡＣ上にいるときは、等積変形で面積は一定。
４×９÷２＝18ｃｍ²

（２）　40.7％
回転図形の底面は円になる。

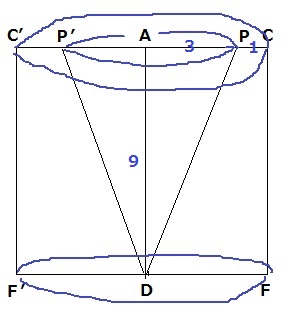
円柱から中にある円錐をひく。
４×４×π×９－３×３×π×９×１/３
＝117πｃｍ³

（３）　7.7％!!

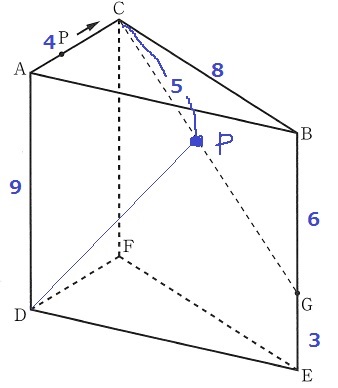
Ｐの位置を確認。
△ＢＣＧは直角三角形なので三平方。
３：４：５で、ＣＧ＝10ｃｍ
ＰはＣＧの中点にあると判明。

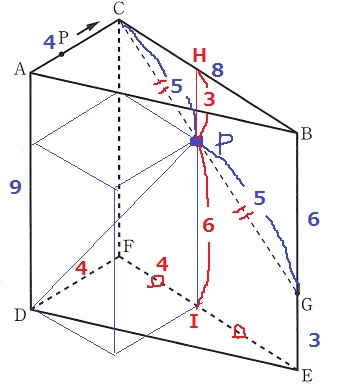
Ｐから垂線をひく。上をＨ、下をＩとする。
さらに、ＤＰを対角線とする直方体を作成。
この直方体の３辺の長さがわかればＤＰがわかる。
*長さがａ、ｂ、ｃである直方体の対角線＝√（ａ²＋ｂ²＋ｃ²）

△ＣＰＨ∽△ＣＧＢ⇒ＨＰ＝６÷２＝３ｃｍ
ＰＩ＝９－３＝６ｃｍ
ＨはＣＢの中点にあるので、ＩもＦＥの中点。
ＤＰ＝√（４²＋４²＋６²）＝√68＝２√17ｃｍ

大問６（関数）

（１）　80.2％
ｙ＝ａｘ²に代入。
ｘ＝０のとき、最小値ｙ＝０
ｘ＝５のとき、最大値ｙ＝25ａ
０≦ｙ≦25ａ
原点に注意！

（２）　61.4％
②はｙ＝ｘ²のグラフ。
Ｃ（２、４）
これをｙ＝５/２ｘ＋ｂにあてはめ。
４＝５/２・２＋ｂ
ｂ＝－１
ｙ＝５/２ｘ－１

（３）　18.0％！
説明の記述も求められる。
CとDはｙ軸を対称の軸として対象関係→D（－２、４）
ｙ＝ａｘ²から、A（－３、９ａ）、Ｂ（２、４ａ）
四角形ＤＡＥＣにおいて、Ｅだけ座標がわかっていない。

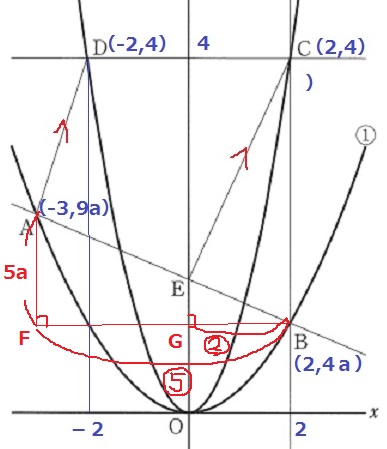
△ＡＦＢ∽△ＥＧＣ
ＥＧ＝５ａ×２/５＝２ａ
Ｅのｙ座標は、２ａ＋４ａ＝６ａ

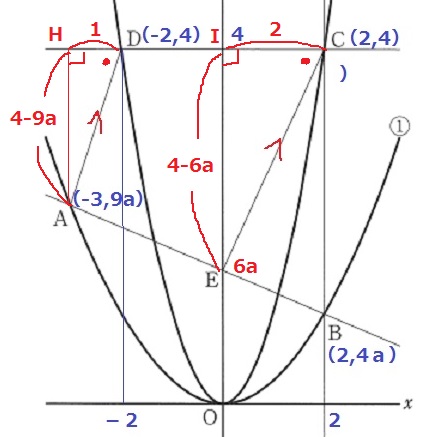
△ＡＤＨ∽△ＥＣＩ（垂直と同位角から２角が等しい）
ＡＨ：ＥＩ＝ＤＨ：ＣＩ＝１：２
ＡＨ＝４－９ａ、ＥＩ＝４－６ａだから、
２（４－９ａ）＝４－６ａ
12ａ＝４
ａ＝１/３

大問７（平面図形）

（１）　33.8％
△ＤＡＣ∽△ＧＥＣの証明。
辺の情報がないので、角度で攻める。

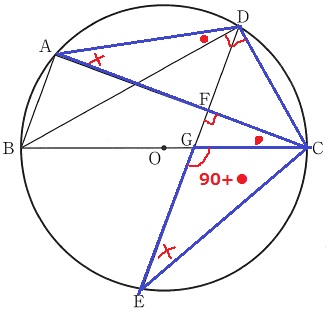
弧ＣＤの円周角＝×
弧ＡＢの円周角＝●
△ＣＦＧで外角定理を使う。∠ＣＧＢ＝90＋●
半円の弧に対する円周角は90°で∠ＢＤＣ＝90°、∠ＣＤＡ＝90＋●
２角が等しい→∽

（２）　14.9％！
ＡＤ：ＤＣ＝３：２なので、これらの円周角に注目する。

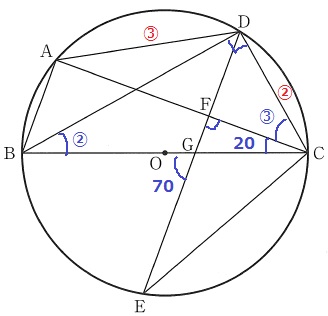
△ＦＧＣで、∠ＦＣＧ＝180－（90＋70）＝20°

∠ＡＣＤ＝③、∠ＣＢＤ＝∠②
∠ＢＤＣ＝半円の弧に対する円周角＝90°
△ＢＣＤで、∠ＡＣＤ＝（180－90－20）×３/５＝42°
△ＣＤＦで外角定理→∠ＣＤＥ＝90－42＝48°
公立高校入試解説ページに戻る