2019年度　清風南海中学過去問Ａ入試【算数】大問４解説

問題ＰＤＦ
Ａ、Ｂ、Ｃの３つの箱があります。
最初にＡ、Ｂの箱に入っているカードの枚数の合計は120枚で、Ｃの箱にはカードが入っていません。
以下のように〔操作１〕、〔操作２〕を定めるとき、次の問いに答えなさい。
〔操作１〕
Ａの箱から１枚、Ｂの箱から２枚カードを取り出してＣの箱にその３枚を入れる。
〔操作２〕
Ａの箱から３枚、Ｂの箱から２枚カードを取り出してＣの箱にその５枚を入れる。

（１）
〔操作１〕を４回、〔操作２〕を６回行ったところ、Ｂの箱のカードの枚数は55枚になりました。
このとき、最初にＡの箱に入っていたカードの枚数を求めなさい。

（２）
〔操作１〕を10回行ったところ、Ａ、Ｂの箱のカードの枚数は同じになりました。
このとき、最初にＡの箱に入っていたカードの枚数を求めなさい。

（３）
〔操作１〕と〔操作２〕を合わせて34回行ったところ、
Ａ、Ｂの箱のカードを同時にちょうど取りきることができました。
このとき、〔操作１〕は何回行いましたか。

（４）
〔操作１〕と〔操作２〕を合わせて何回か行ったところ、
Ａ、Ｂ、Ｃの箱に入っているカードの枚数はすべて同じになりました。
最初のカードの枚数がＡよりＢの方が多いとき、最初にＡの箱に入っていたカードの枚数を求めなさい。

（２）

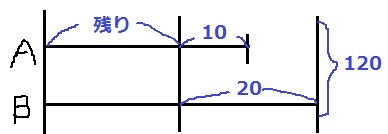
残りのところが同じ。
残り＝（120－30）÷２＝45枚
Ａの最初の枚数は、45＋10＝55枚

（３）
ＡとＢを一体化して考える。
操作①で計３枚、操作②で計５枚取られ、34回の操作で120枚が取られた。
鶴亀算。

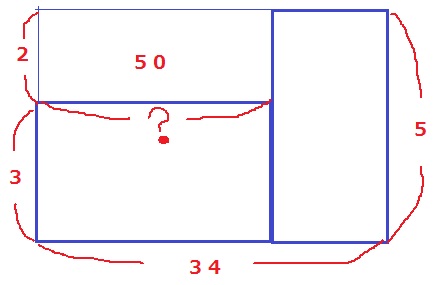
横が操作の回数、縦が１回の操作で抜かれるカードの枚数。
太線の長方形２つの面積が120枚。
左上の長方形の面積は、34×５－120＝50
？＝50÷（５－３）＝25回

（４）
Ａ、Ｂ、Ｃが同数⇒120÷３＝40枚ずつとなる。
操作①では計３枚、操作②では５枚取られる。
操作②の回数で場合分けをし、合計が40枚となるパターンを探す。

操作①×０＋操作②×８＝40枚
操作①×５＋操作②×５＝40枚
操作①×10＋操作②×２＝40枚

問題文より、最初のカードの枚数はＡ＜Ｂで、
ＡとＢが同数となるには、ＡよりＢが多く取られる操作①の回数が多くなる。
⇒操作①×10回＋操作②×２回
Ａは操作①で１枚、操作②で３枚取られるので、
40＋１×10＋３×２＝56枚
難関中 （算数科）解説ページに戻る