平均46.5点(前年比;-5.4点)
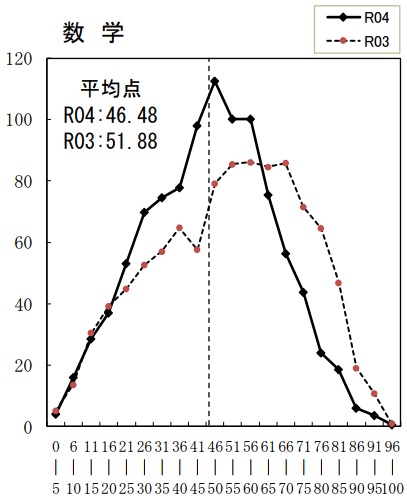
100点―0人、0点―5人
問題はこちら→東進ハイスクールさん(解答)
大問1(小問集合)
(1)
5+(-2)
=5-2
=3
(2)
(-6x+9)÷3 ←分配法則
=-6x÷3+9÷3
=-2x+3
(3)
84を素因数分解する。
84=22×3×7
『ある自然数の2乗』→平方数→各素因数が偶数個。
3と7を1個ずつ追加すればいい。
n=3×7=21
(*84×21=22×32×72=(2×3×7)2=422)
(4)
x2=4x
x2-4x
=x(x-4)=0
x=0、4
ウ
*x2=4xの両辺をxで割らないこと!
x=0のときは割れない。÷0は×!
(5)
集めたお金…500a円
花束の代金…b円
代金より200円足りなかったので、500a=b-200
エ
*「足りなかった」に引き寄せられて不等号にしないこと!
500a<bに200円の情報をつけると、500a+200=b→500a=b-200
(6)
16個の中央値(メジアン)は8番目と9番目の平均値。
15と19の平均で17分
(7)
余事象
〔全体-起こる確率=起こらない確率〕
1-3/8=5/8
(8)
√4<√6<√9
√4=2、√9=3だから、√6は2と3のあいだ⇒整数部分は2。
√6の小数部分a=√6-2
a(a+2)
=√6(√6-2)
=6-2√6
(9)
反比例の比例定数aは積xyで一定。
500W×180秒÷600W=150秒=2分30秒
@余談@
yは秒だが分でもできる。
500W×3分÷600W=5/2分=2分30秒
(10)
合同な4つの図形に分ける⇒4等分
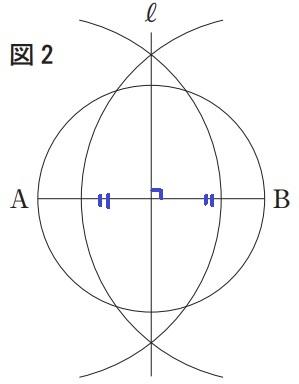
ABの垂直二等分線が答え。
(11)①
∠BOCは弧BCに対する中心角で、∠xは円周角。
120÷2=60°
②
6×6×π×120/360=12πcm2
大問2(小問集合2)
(1)①
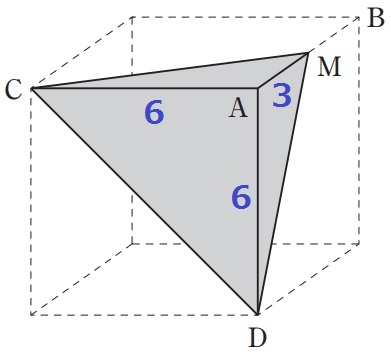
ネジレ→延長しても交わらない、かつ平行でもない。
該当する辺に×を書いてみよう。
AかDと交わるものに×をつけるとCMしか残らない。
ADと平行でもないのでCMが答え。
②
素直な問い。
6×3÷2×6÷3=18cm3
(2)①
捕獲した30匹のうち、印つきは9匹。
⇒全体:印つき=30:9=⑩:③の割合。
印つきは全部で50匹なので、50×⑩/③=166…≒170匹
②
標本調査は母集団のなかから無作為に標本を抽出して、母集団の傾向を推し量る。
対して、全数調査は調査対象すべてを調べ上げる。
世論調査や視聴率は標本調査で足りる。
ア・エ
*歯科検診や健康診断は各人のデータをとらなくては意味がないので全数調査。
総務省が行う国勢調査は全数調査の代表例として覚えておこう。
@テレビの視聴率@
標本(サンプル)の大きさはどの程度求められるか。
大学レベルの統計学の知識が必要だと思うのでサボにはわかりませんが、
テレビの視聴率を計測する機器が設置されている台数の割合は、
全体の0.01%にも満たないようですw( ゚Д゚)w
視聴率調査に協力している人を全く見掛けない理由(ねとらぼ)
↑この記事によると、2017年10月時点で調査対象世帯は全体の0.00005%以下となっている…。
それだけで残りの99.999…%以上を推し量って良いものなのか疑問に思われますが、
統計学的には十分信頼するに足りるサンプル数なんだとか・・。
どうやら母集団が大きくなるほど、標本の大きさは思ったより小さくても間に合うようです。
反対に母集団が小さいと(例えば1クラスのなかの動向では)多くの標本をとらないといけない。
(3)①
xが2014年のゴミ排出量、yが2019年のゴミ排出量。
1つ目は排出量で等式。x-y=200
2つ目は2019年の資源ゴミで等式を立てる。
右辺の『25/100y』は、2019年のゴミ排出量ygに帯グラフの資源ゴミ25%をかけている。
つまり、2019年度における資源ごみの排出量である。
②
今度は『2019年の資源ゴミは2014年と比べて25%増』を使う。
2014年の資源ゴミの排出量は16/100x。
これの25%増(=125%)が2019年の資源ゴミ排出量に相当する。
16/100x×125/100
③
解答では数値を示して説明をする。
問われているのは『可燃ゴミの排出量の比較』
割合は66%→70%に増えているが、可燃ゴミの排出量を知るにはゴミ排出量の合計が必要。
前問の連立を解く。
x-y=200 …①
16/100x×125/100=25/100y …②
②を整理すると、4x=5y…③
①を4倍して、4x-4y=800
これに③を代入すると、5y-4y=y=800
①に放り込んで、x=800+200=1000
ゴミ排出量の合計は2014年が1000g、2019年が800gである。
2014年の可燃ゴミ…1000×66%=660g
2019年の可燃ゴミ…800×70%=560g
可燃ゴミの排出量は減っている。イ
大問3(数量変化・関数)
Ⅰ(1)
あ:60<65≦70だから1000円。
い:1300円まで支払える。最大で100cm以下。
イ
(2)
答案では理由も記述する。
『yはxの関数である』→xの値を決めるとyの値がただ1つに決まる関係。
これを本問にあてはめると、
【荷物の大きさが決まると料金がただ1つに決まる】ので、
料金は荷物の大きさの関数である。ア
*荷物の大きさは料金の関数ではない点に注意!
料金がわかっても荷物の大きさは判明しない。
(3)
●A社→100<115≦140だから1800円。
●B社→超過分は、115-80=35cm
『10cmごと』なので30<35≦40、すなわち超過分は40cmで計算する。
900+200×40/10=1700円
B社の方が100円安い。
Ⅱ(1)
y=ax2について。
ア:a>0だから下に凸。x=0のとき最小値y=0。〇
イ:aの絶対値が大きくなるとグラフは閉じていく。×
ウ:変化の割合は(yの増加量)÷(xの増加量)で一定ではない。〇
*xの値がp→qに増加するときの変化の割合はa(p+q)
エ:双曲線は反比例。×
オ:y=ax2は下に凸、y=-ax2は上に凸でx軸について対称。〇
ア・ウ・オ
(2)
y=-2x+6にx=-6を代入する。
y=-2×(-6)+6=18
y=ax2に(x、y)=(-6、18)を代入。
18=36a
a=1/2
(3)①
AB:BD=1:3をどう使うか。
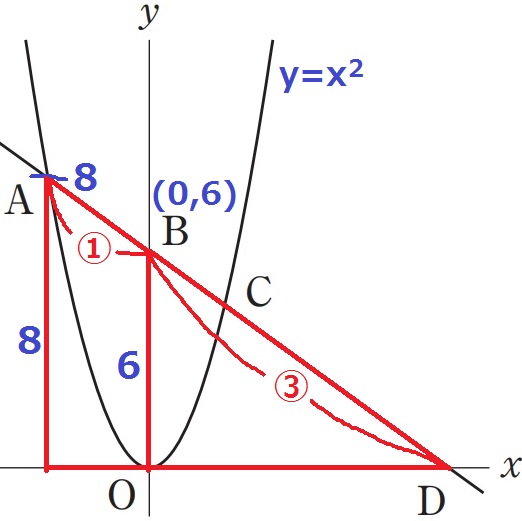
赤線の相似からAのy座標は、6×④/③=8
y=x2にy=8を代入して、
x2=8
Aのx座標は負なのでx<0→x=-2√2
A(-2√2、8)
②
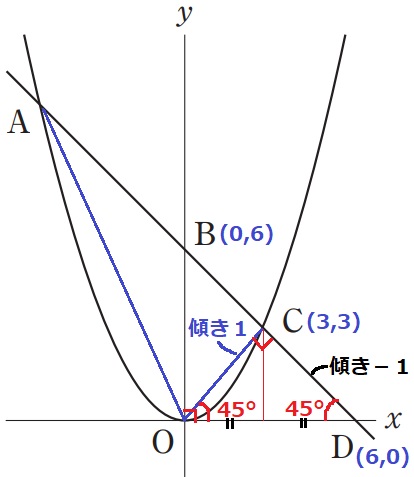
ADの傾きは-1
△OBDは直角二等辺三角形で、OB=OD=6→D(6、0)
また、ADとCで直交するOCの傾きは1、△OCDも直角二等辺三角形。
CはBDの中点にあたる⇒C(3、3)
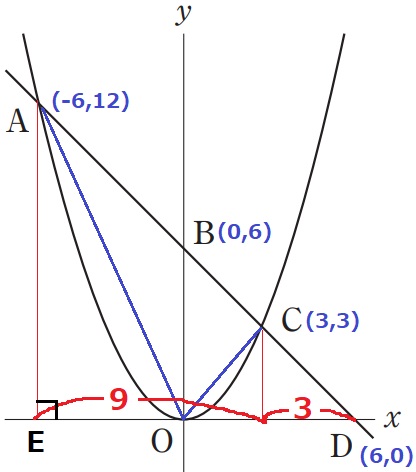
△AOCは面積27、高さBO=6なので、
幅に当たるAとCのx座標の差は27×2÷6=9
Aから垂線をおろし、x軸との交点をEとする。
△ADEも直角二等辺三角形で、AE=DE=9+3=12
Aのy座標は12、x座標は3-9=-6
A(-6、12)
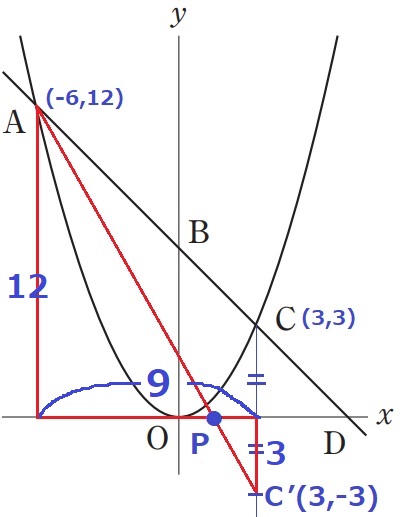
△APCの周の長さが最も短くなるPの位置を考える。
AとCは定点ゆえ、ACの長さは不変。AP+PCの最短を考えればいい。
最短⇒直線。線対称を用いる。
x軸についてCを対称移動させた点をC’とする。AC’とx軸との交点がPである。
赤線の相似に注目して、相似比は12:3=④:①
Pのx座標は、-6+9×④/⑤=6/5
@内分点の公式@

高校数学の美しい物語より。高校数学で習いますが、小技として知っておくと便利です。
Pは(-6、0)と(3、0)を4:1に内分する点なので、
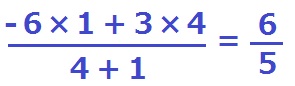 となります。
となります。
大問4(平面図形)
Ⅰ(1)
△BCDの内角は30°―60°―90°で、辺の比は1:2:√3。
斜辺BC=6cmなので、BD=6×√3/2=3√3cm
(2)
△EBF∽△FCDの証明。
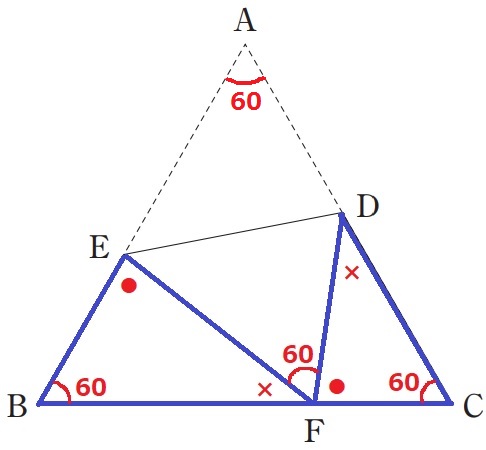
折り返しで、∠EFD=∠EAD=60°
●+×=120°で角度調査。2角が等しいので∽
(3)①
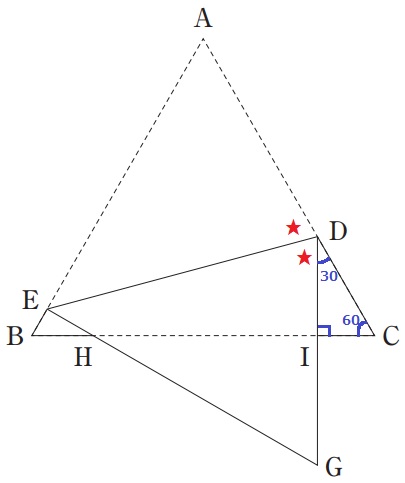
∠CDI=180-(90+60)=30°
折り返しで★は等しい。
∠EDG=(180-30)÷2=75°
②
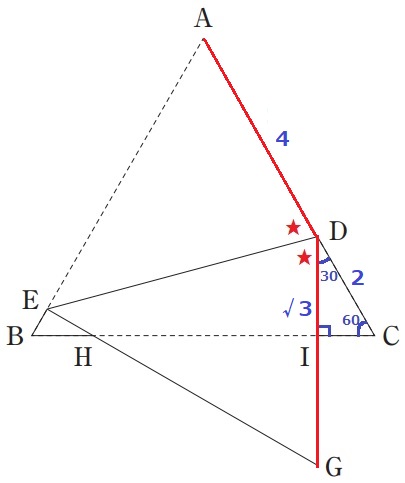
△DCIの辺の比は1:2:√3→DI=√3cm
AD=6-2=4cm
折り返しで、GD=AD=4cm
GI=GD-ID=4-√3cm
Ⅱ(1)①
方針1の相似は使わない!
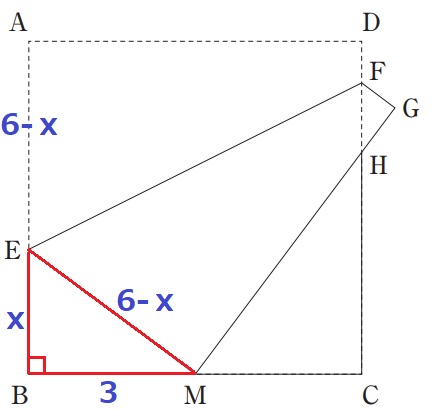
BM=6÷2=3cm
折り返しで、AE=ME=6-xcm
△BEMで三平方。
(6-x)2=9+x2
12x=27
x=9/4
BE=9/4cm
②
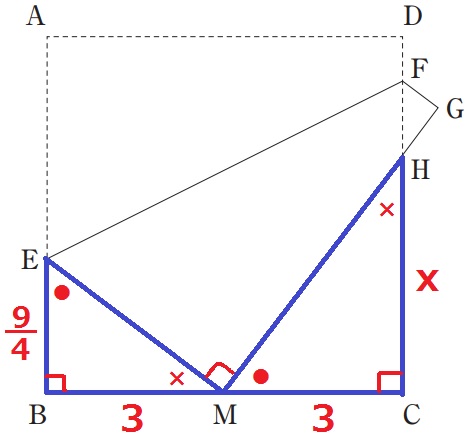
△BEM∽△CMHより、9/4:3=3:x
外項と内項の積で、9/4x=9
x=4
HC=4cm
(2)
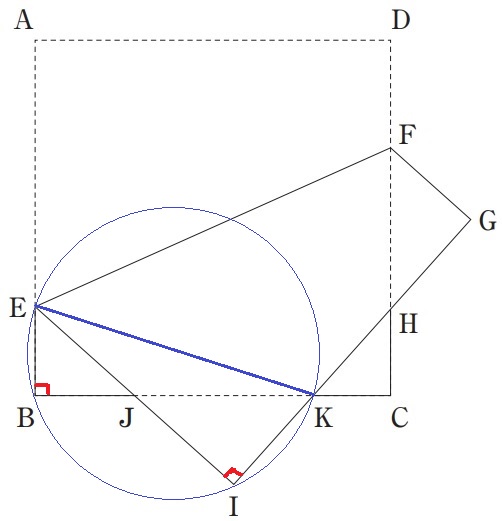
半円の弧に対する円周角は90°
∠EBK=∠EIK=90°より、直径はEKである。

下半分だけをピックアップ。
EB=6×1/4=3/2cm
折り返しで、EI=6-3/2=9/2cm

Iを通るBCに平行な線をひき、EとKの垂線との交点をそれぞれO、Pとする。
△EJB∽△EIO、EJ:JI=1:1より、BO=3/2cm
ここで、△EIOの辺の比に着目する。
EO:EI=3:9/2=②:③
三平方の定理を用いて、OI=〇√5

△EIO∽△IKPより、IK:KP=③:〇√5
KP=3/2cmなので、IK=3/2×③/〇√5=9/(2√5)cm
最後に△EKIで三平方。

直径EK=9√30/10cm
●講評●
大問1
基本レベルで配点36点。
平均46.5点でしたけど、おさえるべきところをおさえればもう少し取れたはず|-`)
(4)数学的に÷0はタブー。x≠0でない限り、xでは割れない。
(8)平方数から整数部分をまず確定する。
大問2
(1)(2)は取りたい。
(3)それぞれのゴミ合計→それぞれの可燃ゴミ。
評価上の留意事項によると、可燃ゴミの660g、560gを正答扱いにし、
連立方程式の解であるゴミ合計の1000g、800gの記述はなくて良いらしい。
大問3
Ⅰ(2)関数の定義。数学用語をきちんと理解しているか。
(3)超過分は30ではなく40cmで計算する。
Ⅱ(3)①求めたいのはAの座標。1:3から先にy座標がわかる。
②やるべきことが多くて大変。
△AOC=27から何がわかるか。まずはAとCの座標を確定する。
そのうえでAP+PCの最短(線対称)にもっていく。
大問4
Ⅰ(3)折り返しは等角と等辺を意識する。
Ⅱ(1)①相似は使わない!折り返し⇒三平方の使用は他県にも出てくる。
②ここで相似。
(2)EKはわかりやすいが、計算がやりづらい。
数値が汚いので処理能力も問われる。
もちろん、△EKBでもできる。
どうすれば複雑な根号計算を回避できるか思案したところ、
中点Jと前問の相似形を頼りに△EKIに着目した。




コメント