平均48.8点(前年比;+4.3点)
問題はこちら→東進ハイスクールさん(解答)
大問1(小問集合)
(1)①
1+2×(-4)
=1-8
=-7
②
3x-1/2x
=5/2x
③
4a2b÷2a×2b
=4ab2
(2)
絶対値…数直線上で原点0からの距離。
小数に変換してみよう。
ア:3.2 イ:-3.5
ウ:√2→1.41421356…(人夜人夜に人見頃)
2√2≒2.82
エ:3.33… オ:-3
絶対値が最も大きいのはイ。
(3)
x2-10x+25
=(x-5)2
(4)
2x+3y=4 …①
-x+y=3 …②
①+②×2
2x+3y=4
+)-2x+2y=6
5y=10
y=2
②に代入。-x+2=3
x=-1
x=-1、y=2
(5)
全体…2×2×2=8通り
〔少なくとも1回は表=全体-全部裏〕
全部裏は1通りしかない。
確率は7/8
(6)
(2x-5)2=18 ←展開しないで2乗を消す。右辺は根号
2x-5=±3√2
2x=5±3√2
x=(5±3√2)/2
(7)
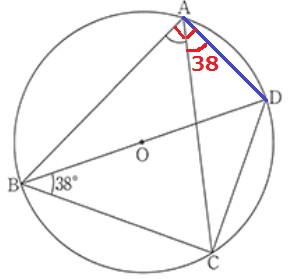
ADに補助線。
弧CDに対する円周角より、∠CAD=38°
半円の弧に対する円周角より、∠BAD=90°
∠BAC=90-38=52°
(8)
取り出した100個のうち、黒:白=90:10=9:1
この割合は母集団も変わらないとみなす。
容器の中に白は全部で100個あったので、
黒の個数は、100×9/1=900個 →ウ
(9)
同位角か錯角が等しければ、2直線は平行。
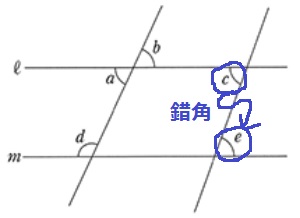
∠cと∠e
大問2(関数の性質)
(1)
ア:x=1、2、3、4、5をやってみると、y=1、2、2、3、2でバラバラ。
イ:y=-x+1000(一次関数)
ウ:y=1200/x(反比例)
エ:食塩=食塩水×濃度→y=0.05x
オ:y=2x
エ・オ
(2)
ア:y=ax2は原点を通過する。
イ:x>0のときxが増加するとyも増加。
x<0のときはxが増加するとyは減少。
ウ:y軸に対して左右対称。
エ:x=0のとき、最小値y=0、x=2のとき、最大値y=8
オ:比例や一次関数であれば変化の割合は変わらないが、放物線の場合は変わる。
y=ax2において、xの値がp→qに増えたときの変化の割合はa(p+q)
ア・エ
大問3(整数の証明)
千の位…a、百の位…b、十の位…b、一の位…a(aは1桁自然数、bは1桁自然数or0)
4桁の自然数は、1000a+100b+10b+aと表せる。
11の倍数であることを証明したいので、最後は11でくくる形にもっていく。
1000a+100b+10b+a
=1001a+110b
=11(91a+10b)
91a+10bが整数だから、11(91a+10b)は11の倍数。
したがって、このような4桁の整数は、いつでも11の倍数となる。
@余談@
去年の栃木大問2(2)では誘導穴埋め問題で同じ題材がでた。
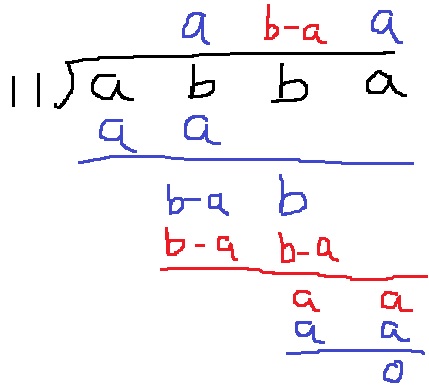
↑筆算で確かめることができます。
@11の倍数@
覚える必要性は乏しいですが、11の倍数にはルールがあります。
〔各位を交互に足し引きして11で割れたら11の倍数〕
505582だったら、、
5-0+5-5+8-2=11 →505582は11の倍数
言い換えれば、奇数の位(一、百、万…)の和と偶数の位(十、千、十万…)の和を合算して、
11の倍数だったら11の倍数。
11で割ったときの余りに注目します。
奇数の位は、1=11×0+1、100=11×9+1、10000=1111×9+1
偶数の位は、10=11×1-1、1000=11×91-1、100000=11×9091-1
+1と-1で相殺すれば、余りがなくなって11の倍数になる。
〔abba〕だったら、(a+b)-(b+a)=0
0も11の倍数(11×0)だから、abbaは11の倍数。
専修大松戸で丁寧な誘導付きで仕組みを紐解く問題がでました。
大問4(空間図形)
(1)
1辺がa、b、cの直方体の対角線の長さ→√(a2+b2+c2)
√(22+42+32)=√29m
(2)①
展開図を別々に書いて調べる。

ア:√41m
イ:√45(3√5)m
ア・√41m
②
長い方なので、イを選択する。
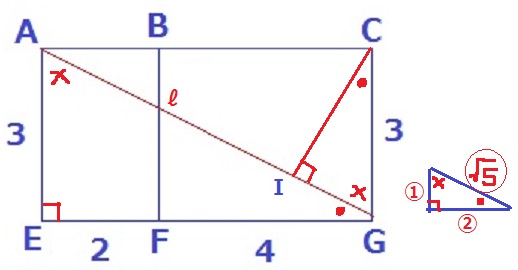
Cからおろした垂線と直線ℓとの交点をIとする。
●+×=90°で調べていくと、2角相等で△AEG∽△GIC
直角三角形の辺の比は3:6:3√5=1:2:√5なので、
CI=3×2/√5=6√5/5cm
大問5(平面図形)
(1)
正確な作図力を要する。
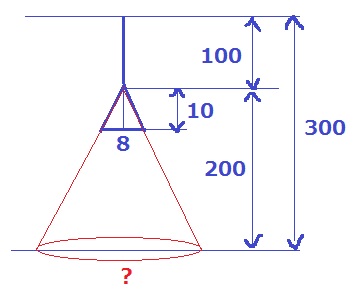
ライトが床を照らす円の直径は、8×200/10=160cm
(2)①
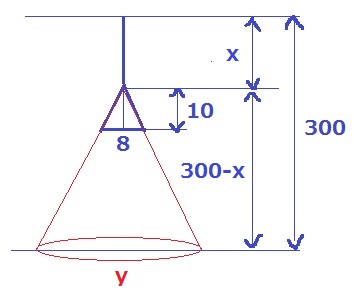
先ほどの図をxとyに変換。
y=8×(300-x)/10
=240-4/5x
y=-4/5x+240
②
x=50のとき、y=-4/5×50+240=200
x=180のとき、y=-4/5×180+240=96
96≦y≦200
*ヒモの長さ(x)が短いほど、照らされる面積は広くなる。
(3)

ライトA・Bの高さと直径の比を表すと、うえのようになる。
床が照らされた円の面積が等しくなるということは、④=△3
最小公倍数12で比を統一する。

1/2x=□20-□15=□5
300m=□25で、x=□10だから、
x=300×10/25=120
大問6(平面図形2)
(1)①
ABの中点Oを作図する。
ABの垂直二等分線を描き、直径ABとの交点がO。
②
説明問題。方針は立てやすい。
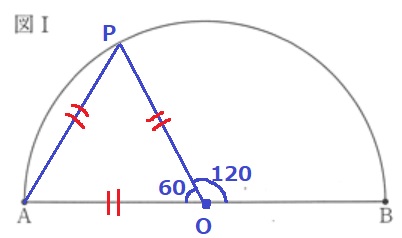
仮定と半径から、△AOPの3辺が等しい→△AOPは正三角形。
∠AOP=60°
∠BOP=120°
弧の長さは中心角に比例するので、弧AP:弧PB=60:120=1:2
(2)①
円折り返し問題(;´Д`)
2015年度の群馬大問5でも出題され、苦戦しました。
折り返した半円と直径ABとの交点が、
なんとなく中心Oとかぶっているような気がする。
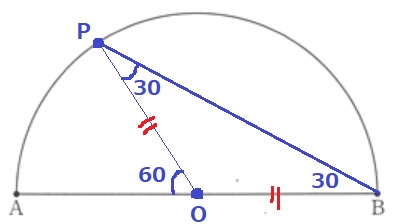
△PBOは半径より二等辺。
外角定理から、∠OPB=∠OBP=60÷2=30°
PBで折り返したとき、弧PBと直径ABとの交点はどこにくるのだろう?
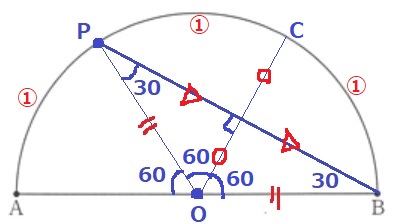
PBの垂直二等分線をひき、円周との交点をCとする。
この線分は中心Oを通る。
なぜなら、三角形の内角は30°と90°なので、残りの角(中心角)は60°となり、
二等辺三角形PBOを垂直に二等分する。
また、Cは弧PBの中点にあたるので、弧AP:弧PC:弧CB=1:1:1
→中心角はどれも60°で辻褄が合うから。
PBを対称の軸とすると、OとCは対応する点となる。
以上より、折り返した半円は中心Oで交わることが証明された。
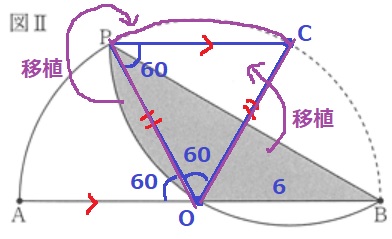
半径と∠POC=60°から、△POCの内角はすべて60°で正三角形。
移植すると、求積すべき図形は半径6cm、中心角60°の扇形となる。
6×6×π×60/360=6πcm2
②
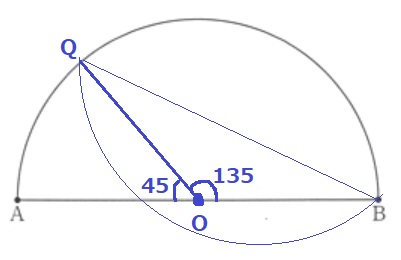
中心角は弧の長さに比例するので、弧AQ:弧QB=1:3から、
∠AOQ=180×1/4=45°
∠QOB=180-45=135°
ここから重なり部分の面積を求めたいが、形が複雑…。
とりわけ、△QBOの左側がよくわからない形をしているので、
折り返した部分の面積から、下の重なっていない部分を引くのでは?と推測する。

折り返し部分を求める。
半径6cm中心角135°の扇形から△QBOをひけばいい。
Qから垂線をおろし、直径ABとの交点をCとする。
△QOCは45°-45°-90°の直角二等辺三角形だから、
1:1:√2より、QC=6×1/√2=3√2cm
折り返し部分の面積…6×6×π×135/360-6×3√2÷2=27/2π-9√2cm2
続いて、下の部分を求めたい。
前問と同様、やはり気になるのは弧QBと直径ABの交点。
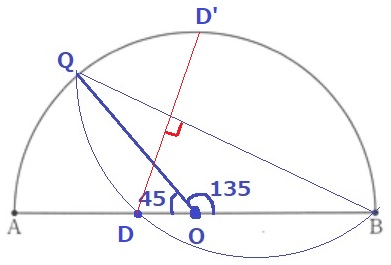
交点をDとする。
対称の軸QBについて、Dと対応する点をD’とおく。
D’Bに補助線を描いてみよう。
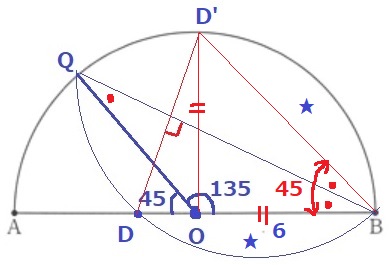
△QBOは二等辺三角形。
外角定理より、●+●=45°
線対称より、∠QBD=∠QBD’なので、∠D’BD=●+●=45°!
半径からOB=OD’なので、△OBD’の内角は45°-45°-90°で直角二等辺三角形!
D’はOの真上にいることになる。
また、線対称から★の面積が等しい。
★の面積は半径6cm中心角90°の扇形から、直角二等辺三角形OBD’を引けばいい。
6×6×π×90/360-6×6÷2=9π-18cm2
求めたい面積は、
27/2π-9√2-(9π-18)
=9/2π-9√2+18cm2
●講評●
後半の図形がキツイ!
前半部分はどうにか死守したい。
大問1~3
教科書や問題集にでてくる問題。
大問4
(2)最短→展開図の作成。2つ書いて調べる必要がある。
②相似関係が見つかりにくいか。90°の処理に慣れて2角相等を導きたい。
大問5
数学を活用した設定で正答率が悪そう。
幾何の基本は作図。照らされる面をきちんと描く。
(3)は厳しい。無理そうなら他に時間をあてよう。
算数的解法だと情報や計算がスッキリしやすい。
大問6
(1)は守りたい。理由説明が曲者だが取りたい。弧の比は中心角の比。
(2)円の折り返しは難しい:;(∩´_`∩);:
他の都道府県の上位層もぜひチャレンジして頂きたい。
不規則な形は移植or分割or周りから引く。
折り返した弧と直径の交点をうまく見極めたい。



コメント