2024年度　長野県公立高校入試問題過去問【数学】解説

平均49.0点（前年比；－2.1点）

100点―１名、０点―16名
問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）
３－（－５）
＝３＋５
＝８

（２）
１/６ｘｙ²÷１/12ｘｙ
＝２ｙ

（３）
８の倍数になる→８でくくれる。
８ｎ＋16
＝８（ｎ＋２）
ｎ＋２は整数だから、８（ｎ＋２）は８の倍数。
エ

（４）
ｘ²－ｙ²
＝（ｘ＋ｙ）（ｘ－ｙ）
＝｛（√５＋√３）＋（√５－√３）｝｛（√５＋√３）－（√５－√３）｝
＝２√５×２√３
＝４√15

（５）
ｘ²－３－10
＝（ｘ＋２）（ｘ－５）＝０
ｘ＝－２、５

（６）
（132＋ｘ）：（12＋ｘ）＝７：２
内項と外項の積から、７（12＋ｘ）＝２（132＋ｘ）
84＋７ｘ＝264＋２ｘ
５ｘ＝180
ｘ＝36

＠別解＠

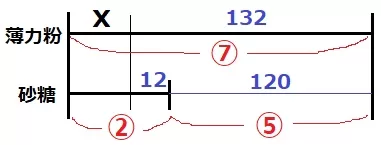
算数では上のような線分図を描き、132－12＝120＝⑤だから、
加えた後の砂糖は、120×②/⑤＝48ｇ
ｘ＝48－12＝36ｇ

（７）

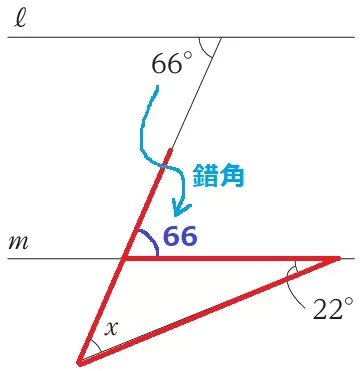
66°を錯角で降ろし、赤線の三角形で外角定理。
ｘ＝66－22＝44°

（８）

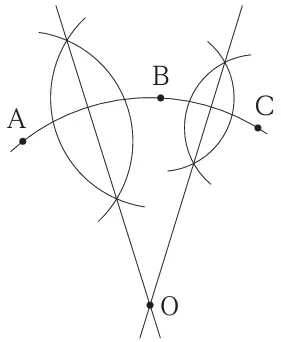
円の中心の作図。
中心Ｏは円周上の３点Ａ・Ｂ・Ｃから等距離にある。
①ＡＢの垂直二等分線→Ａ・Ｂから等距離にある点の集合。
②ＢＣの垂直二等分線→Ｂ・Ｃから等距離にある点の集合。
③２つの直線の交点は３点Ａ・Ｂ・Ｃから等距離にある中心Ｏ。

（９）①

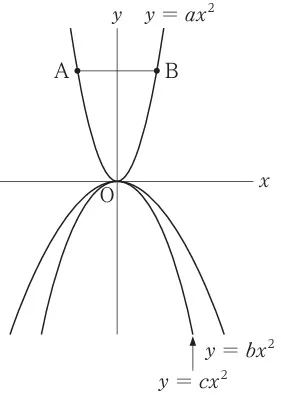
グラフが下に凸→ａ＞０
上に凸→ｂ、ｃ＜０
絶対値が小さいほど、グラフの開きは大きくなる。
ｂの方がグラフの開きが大きい→ｂはｃより絶対値が小さい→ｂとｃは負同士だからｂ＞ｃ
ａ＞ｂ＞ｃ

②

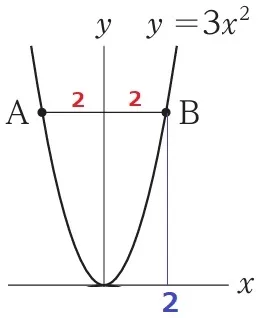
Ｂのｘ座標は、４÷２＝２
これをｙ＝３ｘ²に代入する。
ｙ＝３×２²＝12
Ｂ（２、12）

（10）
奇数⇒一の位が１か３であれば、十・百の位はなんでもいい。
取り出した順に左から並べるが、一度に３枚とって右の一の位から並べても同じ。
一の位が１か３は３枚中２枚。奇数になる確率は２/３

（11）

最小値…24、最大値…50
15人の中央値（Q2）は８番目の値…34
第１四分位数（Q1）は下位７人の真ん中、下から４番目…26
第３四分位数（Q3）は上位７人の真ん中、上から４番目…42
ウ

大問２（総合問題）

Ⅰ（１）①

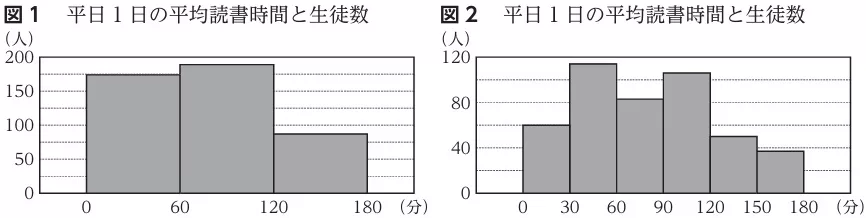
階級の幅が左は60分、右は30分。
ア：図１は150分以上に絞っていないので読み取れない。×
同じ全校生徒のデータなので、150分以上の生徒の人数は同じである。
イ：範囲＝最大値－最小値。いずれの値もヒストグラムからは不明。×
ウ：最頻値は最も表れている値。図１…90分、図２…45分。〇
エ：図１の中央値は60～120分。図２は即断しにくいが、30～60分ではないと推測できる。×
次の度数分布表から、全校生徒の人数は302＋148＝450人
中央値は225番目と226番目の平均で、図２では60～90分の階級に属する。
ウ

②ⅰ
60分未満の生徒は、１・２年が302人中94人、３年が148人中80人。
母数（＝度数の合計）が違う。
イ

ⅱ
データの傾向を調べるので、【う】は最小値や最大値でもなく代表値。
これだけでアと絞れてしまう。。
代表値…平均値・中央値・最頻値などの総称。

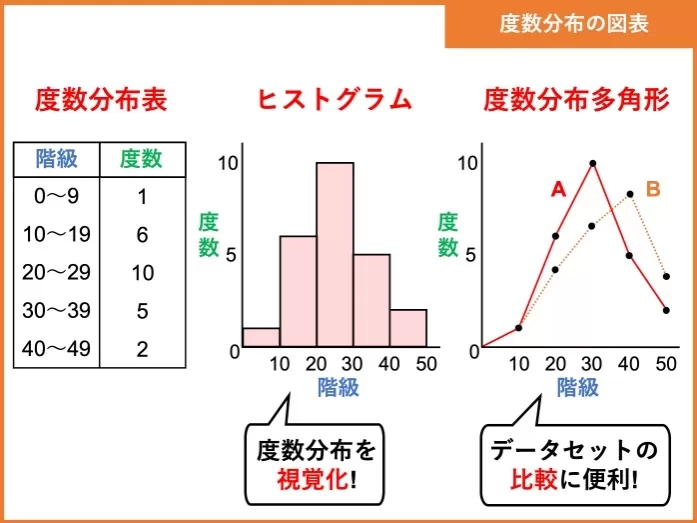
受験辞典より。
度数分布多角形は横に階級、縦に度数や相対度数をとり、その分布を折れ線で示したもの。
度数の合計が異なる複数のデータを比較する際に用いる。
ア

（２）①

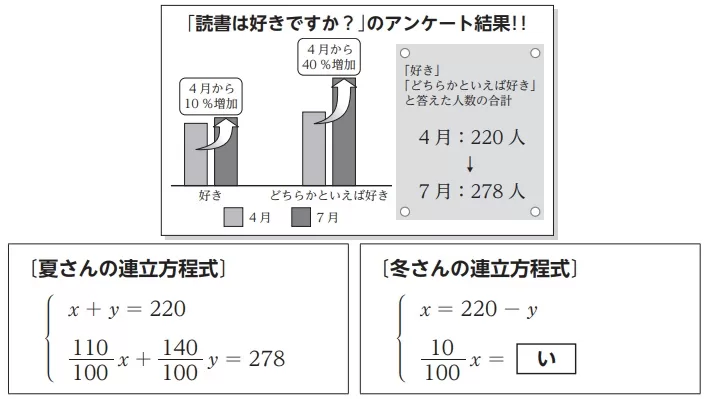
220人の意味は右側に書いてある。
解答例：４月の「好き」「どちらかといえば好き」と答えた人数の合計

＠余談＠
ｘ…４月の「好き」、ｙ…４月の「どちらかといえば好き」の人数
７月の「好き」「どちらかといえば好き」の合計が278人で、
ｘの110％、ｙの140％の和に相当するから、110/100ｘ＋140/100ｙ＝278

②
同様に、冬もｘ…４月の「好き」、ｙ…４月の「どちらかといえば好き」
10/100ｘは「好き」の10％増加分。
→冬は増加する人数に着目している。

増加した人数の合計は、278－220＝58人
「どちらかといえば好き」の増加は40/100ｙ人。
【好きが増えた人数＝増えた人数の合計－どちらかといえば好きが増えた人数】
10/100ｘ＝58－40/100ｙ

③
ｘ＋ｙ＝220　…①
夏の２つ目を100倍→110ｘ＋140ｙ＝27800　…②
②－①×110をすると、30ｙ＝3600
ｙ＝120
①に代入、ｘ＝220－120＝100

４月の好きが100人。７月の好きは、100×110％＝110人
４月…100人、７月…110人

Ⅱ（１）
回転体は半径３ｃｍの球。
【球の体積Ｖ＝４/３πｒ³】
４/３π×３³＝36πｃｍ³

（２）
【球の表面積Ｓ＝４πｒ²】
図４の球の表面積は、４π×３²＝36πｃｍ²

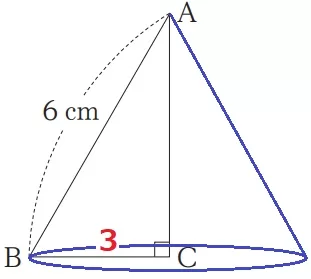
円錐の側面の展開図が半円（中心角180°）になった。
母線：半径の比は中心角（半円180°：円360°）の逆比。
母線：半径＝360：180＝②：①
底面の円の半径は、６×①/②＝３ｃｍ
図５の表面積は、３×３×π＋６×６×π×１/２＝27πｃｍ²
図４の表面積は図５の表面積の36π/27π＝４/３倍

大問３（数量変化・関数）

Ⅰ（１）

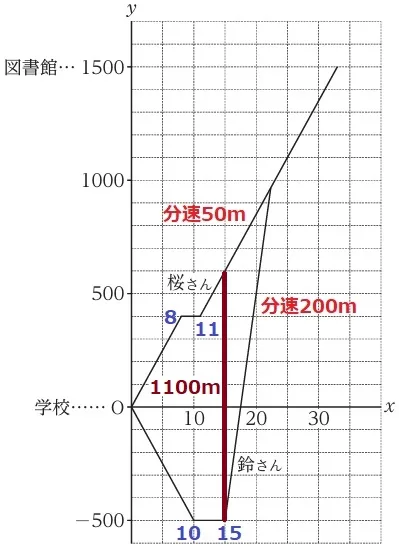
ｙ軸は図書館からの距離。
鈴の家は－500ｍなので、学校を挟んで図書館とは反対方向の500ｍ地点にある。
桜の家は＋400ｍ地点なので、両家は400＋500＝900ｍ離れている。
あ…500、い…900

（２）
桜は11分後に家を出発する。
分速50ｍ→傾き50
（11、400）から左に11、下に11×50＝550ｍ下がるので、
切片は400－550＝－150
直線の式は、ｙ＝50ｘ－150

ｘの変域を求める。左端の点はｘ＝11
右端は図書館に着いた時刻である。
先ほどの式にｙ＝1500を代入する。
1500＝50ｘ－150
ｘ＝33→ｘの変域は11≦ｘ≦33
ｙ＝50ｘ－150、11≦ｘ≦33

（３）
桜が家を出発してから５分後→11＋５＝16分後
鈴が家を出発する15分後において、グラフより両者は600＋500＝1100ｍ離れている。
１分間に200－50＝150ｍずつ差が縮まるから、
16分後の両者の差は、1100－150＝950ｍ

（４）

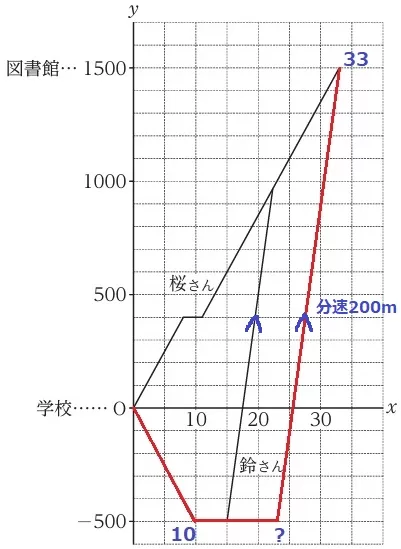
鈴が桜に追いついた時間を33分後にする。
自転車に乗っていた時間は、（1500＋500）ｍ÷分速200ｍ＝10分
鈴が家を出たのは、33－10＝23分後
鈴が家に到着した時刻から、23－10＝13分後

Ⅱ（１）①
反比例は双曲線だが、ｘとｙがともに自然数である点を数える。
格子点は（１、12）（２、６）（３、４）（４、３）（６、２）（12、１）の６個。

②

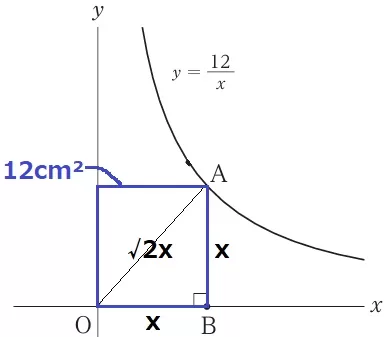
反比例の比例定数ａはｘとｙの積で一定。
ｙ＝12/ｘであれば、Ａから各軸におろした垂線と軸に囲まれた四角形の面積は常に12ｃｍ²になる。
直角二等辺三角形ＯＡＢを２つくっつけた、上図の青い四角形は12ｃｍ²の正方形。
１辺をｘとすると、対角線ＯＡは√２ｘ。

ｘ²＝12
ｘ＞０より、ｘ＝２√３ｃｍ
ＯＡ＝２√３×√２＝２√６ｃｍ

（２）①

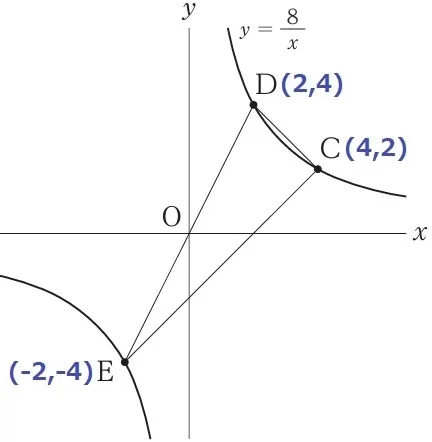
ｙ＝８/ｘにｘ＝２を代入→Ｄ（２、４）
Ｃのｘ座標は４、同様に代入→Ｃ（４、２）
ＤＥは原点Ｏを通る。Ｅは原点についてＤに対称な点→Ｅ（－２、－４）

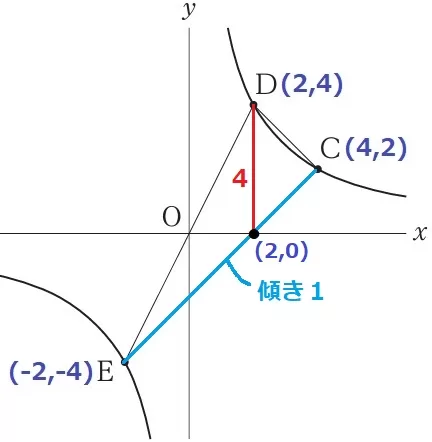
Ｅ（－２、－４）→Ｃ（４、２）
右に６、上に６だから、ＣＥの傾きは１。
Ｃから左に２、下に２移動すると、ｘ軸との交点は（２、０）
ちょうどＤの真下の点である。
Ｅ～Ｃの幅は６ｃｍだから、△ＣＤＥの面積は４×６÷２＝12ｃｍ²

②

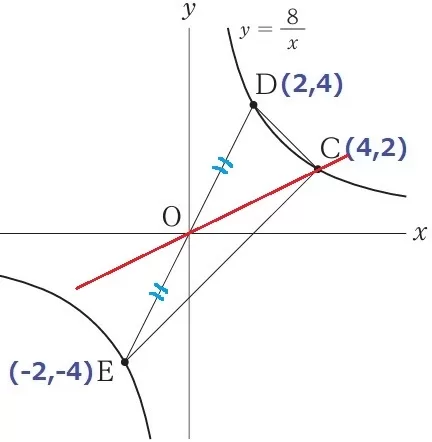
Ｃを通る△ＣＤＥの二等分線→ＤＥの中点Ｏを通過する。
すなわち、ＯＣの式を求めればいい。
ｙ＝１/２ｘ

大問４（平面図形）

（１）

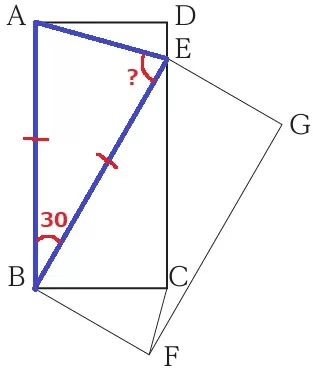
ＡＢが30°回転してＥＢ→ＡＢ＝ＥＢ、∠ＡＢＥ＝30°
△ＡＢＥは二等辺だから、∠ＡＥＢ＝（180－30）÷２＝75°

（２）①
△ＡＢＥ∽△ＣＢＦの証明。

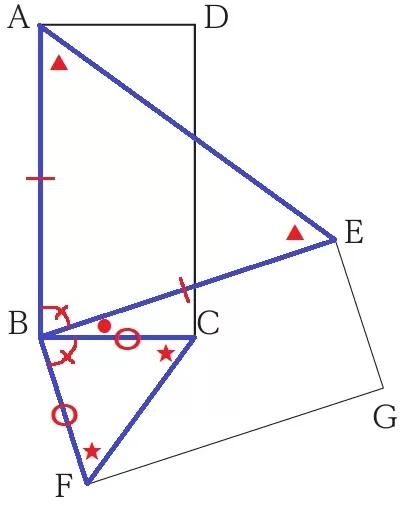
長方形の内角は90°
∠ＡＢＥ＝90－∠ＣＢＥ＝∠ＣＢＦ
∠ＡＢＥ＝∠ＣＢＦ

回転移動の対応する辺から、ＢＡ＝ＢＥ、ＢＣ＝ＢＦ
△ＡＢＥと△ＣＢＦは二等辺三角形である。
２つの底角は等しいので、∠ＢＡＥ＝∠ＢＥＡ（▲）、∠ＢＣＦ＝∠ＢＦＣ（★）

三角形の内角の和は180°だから、それぞれの内角を求めると、
１/２（180－∠ＡＢＥ）＝∠ＢＡＥ（▲）
１/２（180－∠ＣＢＦ）＝∠ＢＣＦ（★）
→▲＝★が成り立つ。二等辺の頂角が等しければ底角も等しい。
２角相等で∽。
あ…∠ＣＢＥ、い…２つの底角、う…180°

②
今度は２辺の比とあいだの角をつかって同様の証明をおこなう。

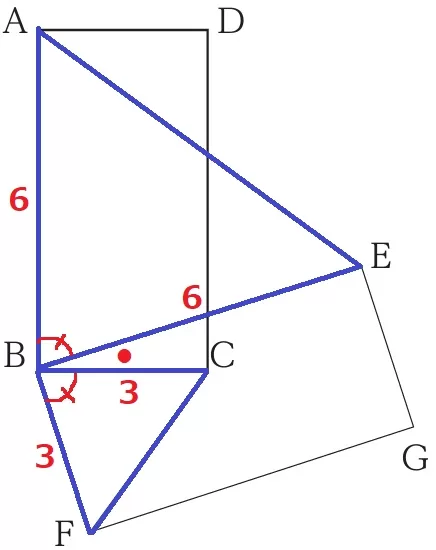
前半は先ほどと重複します。
90－∠ＣＢＥつながりで、∠ＡＢＥ＝∠ＣＢＦ
ＢＡ：ＢＣ＝６：３＝２：１
同様に、ＢＥ：ＢＦ＝２：１
ＢＡ：ＢＣ＝ＢＥ：ＢＦ
２辺とあいだの角が等しいから∽

（３）

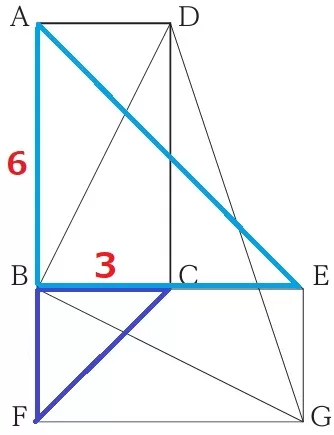
△ＣＢＦ∽△ＡＢＥから、ＣＦ：ＡＥ＝３：６＝１：２

今度はＣＦとＤＧを１辺とする三角形に着目する。
同じ長方形の対角線から、ＤＢ＝ＧＢ

角度調査。
△ＡＢＤと△ＦＧＢは同じ長方形の半分で合同。
●＋×＝90°で等角を打つと、∠ＤＢＧ＝180－（●＋×）＝90°
頂角を90°とする二等辺三角形→△ＣＢＦ∽△ＤＢＧ
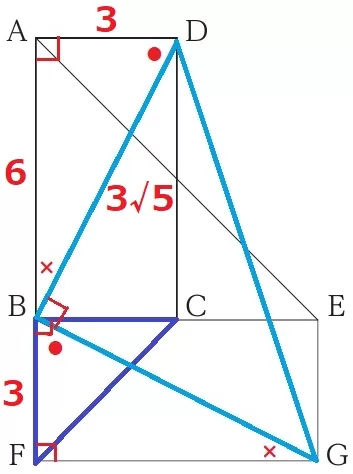
△ＡＢＤで三平方→ＤＢ＝３√５ｃｍ
ＣＦ：ＤＧ＝３：３√５＝１：√５
え…２、お…√５

（４）
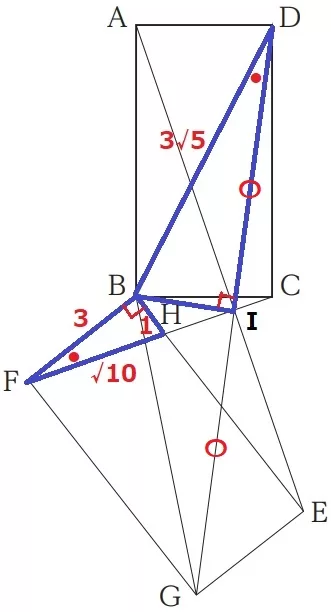
難問。線分が多くて迷子になる。

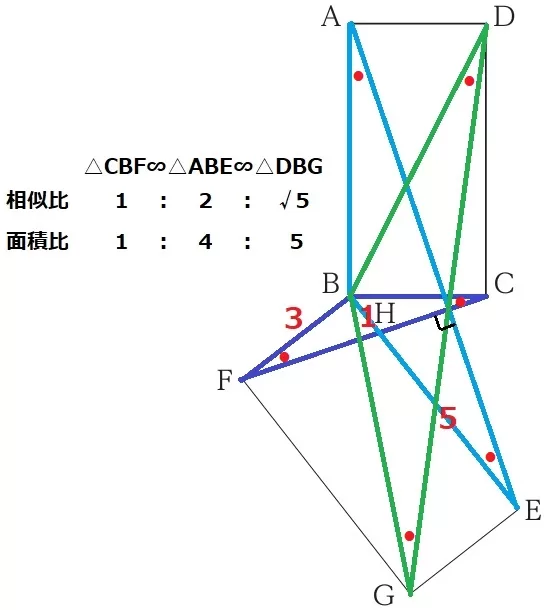
前問の情報を統合すると、△ＣＢＦ∽△ＡＢＥ∽△ＤＢＧであり、
相似比は１：２：√５→２乗して面積比は１：４：５である。

長方形を何度回転させたのかわからない。
ＥＨ＝５ｃｍの情報から要は点Ｈである。
ＢＨ＝６－５＝１ｃｍ
△ＣＢＦ付近に情報が集まっているので、△ＣＢＦ×５＝△ＤＢＧを目指す。
また、△ＡＢＥ→△ＣＢＦに着目すると、ＡＢ⊥ＣＢから対応するＡＥ⊥ＣＦが成り立つ。

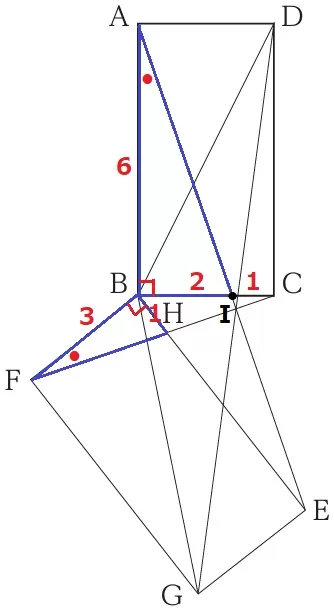
二等辺の底角●を内角に含む直角三角形の辺の比は、△ＢＦＨから１：３である。
ＢＣとＡＥの交点をＩとする。
△ＢＦＨ∽△ＢＡＩより、ＢＩ＝６÷３＝２ｃｍ
ＩＣ＝３－２＝１ｃｍ

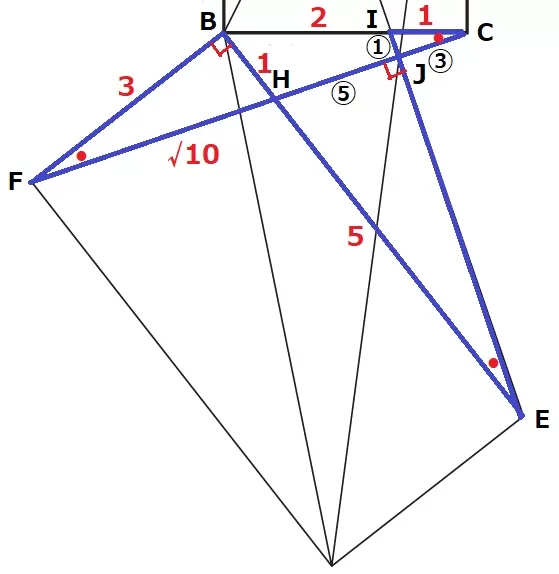
下をピックアップします。ＦＣとＩＥの交点をＪとする。
同様に、●を含む直角三角形に注目すると３つの青い三角形が∽。
最も短いＩＪ＝①とすると、ＪＣ＝③
△ＩＪＣ∽△ＨＪＥの相似比は１：５→ＨＪ＝⑤

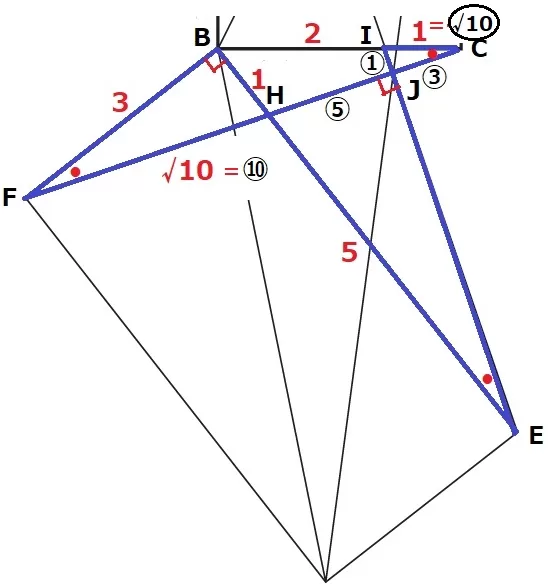
△ＨＢＦで三平方→ＦＨ＝√10ｃｍ
△ＩＪＣの辺の比で三平方をすると、１ｃｍ＝〇√10だから、
ＦＨ＝√10ｃｍ×√10＝⑩
【方針；△ＨＢＦ→△ＣＢＦ→△ＢＤＧ】
３×１÷２×⑱/⑩×５＝27/２ｃｍ²

＠別解＠
お助けマンさんより素晴らしい別解を頂きました。

ＢからＤＧにおろした垂線との交点をＩとします。
△ＢＤＧは二等辺三角形なのでＩはＤＧの中点ですから、△ＩＤＢ×２＝△ＢＤＧとなります。
△ＢＦＨ∽△ＩＤＢに着目します。
相似比は√10：３√５→面積比は２乗して、△ＢＦＨ：△ＩＤＢ＝②：⑨
したがって、△ＢＤＧの面積は、１×３÷２×⑨/②×２＝27/２ｃｍ²
こちらの方が筋道がハッキリしており、模範解答だと思います。