2019年度　青森県公立高校過去問【数学】解説

平均44.1点

満点が１人いた。
問題はコチラ→ＰＤＦファイル

大問１（小問集合１）

（１）ア　98.8％
－８＋６＝－２

イ　65.9％
（－0.5）÷２/７
＝－１/２×７/２
＝－７/４

ウ　73.9％
ａ＋３ｂ－２
－)ａ－ｂ＋４
４ｂ－６

エ　70.7％
（ｘ－２）²－（ｘ－１）（ｘ＋４）
＝ｘ²－４＋４－ｘ²－３ｘ＋４
＝－７ｘ＋８

オ　81.3％
√３－９/√３ー√12
＝√３－３√３－２√３
＝－４√３

（２）　60.9％
２ａ＋３ｂ≦2000

（３）　70.2％
計算してから代入。
６ａｂ²×（－ａ）²
＝６ａ³ｂ²
＝６×（－２）³×（－１）²
＝６×（－８）×１＝－48

（４）　65.3％
因数分解できないので解の公式。
ｘ＝（－１±√13）/２

（５）　46.0％
『少なくとも１人は当たる』→全体－２人とも外れ。
２人が外れる確率は、〔５本から２本の外れ〕→〔４本から１本の外れ〕。
２/５×１/４＝１/10
１－１/10＝９/10

（６）　47.7％
Ａ：Ｂ＝②：⑤
差が③で、移した量は半分の○1.5。
全体の⑦が、42×２＝84Ｌに相当するので、
84×○1.5/⑦＝18Ｌ

（７）　49.1％
△ＡＢＣで外角定理。
●＋●＋42＝×＋×　…①
①÷２
●＋21＝×　…②

△ＤＢＣで外角定理。
●＋ｘ＝×　…③
②と③から、ｘ＝21°

（８）　55.8％

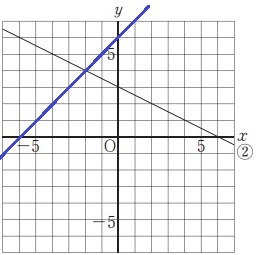
青線がｙ＝ｘ＋６
交点の座標が答え。ｘ＝－２、ｙ＝４

大問２（作図・標本調査）

（１）　70.9％
Ａを通るＢＣに垂直な線を描く。
①Ａを中心に適当な弧を描く。
②ＢＣとの交点を中心に適当な弧をそれぞれ描き、その交点とＡを結ぶ。

（２）ア…47.2％　イ…28.7％！
降順に直す。
Ｃ－９、Ｉ－８、Ｆ・Ｈ－７、Ｂ－６
Ａ－３、Ｄ－２、Ｅ・Ｊ－１

【Ｇは平均値より上だが、順位は真ん中より下】
ということは、Ｃ～Ｂがベスト５確定。
Ｇは５以下の値が候補となる。

Ｇ以外の和（表の値の合計）は４４。
あとは地道に代入して平均を出す。

Ｇ＝５のとき、（４４＋５）÷10＝4.9
Ｇ＝４のとき、（４４＋４）÷10＝4.8
Ｇが４以下だと平均を下回る。
よって、Ｇは５回で平均は4.9回。
ア…５　イ…4.9

大問３（図形）

（１）ア　30.4％！

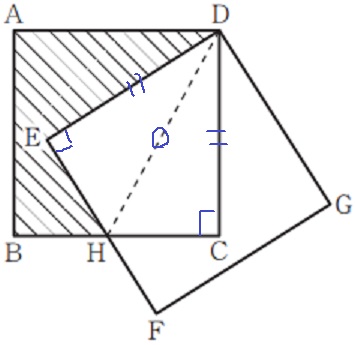
直角三角形の合同条件である、斜辺と他の１辺が等しい点を指摘する。

イ　10.0％！

ＢＨ：ＨＣ＝２：３
高さが等しければ、辺の比が面積比となる。
△ＤＢＨ＝②、△ＤＨＣ＝③。
前問の合同から、△ＤＨＥ＝③
正方形ＡＢＣＤの面積は、（②＋③）×２＝⑩
斜線部分は、⑩－⑥＝④
正方形の面積は、20×⑩/④＝50ｃｍ²
１辺の長さは、√50＝５√２ｃｍ

（２）ア　52.4％
５×５×π×２＋５×２×π×10
＝150πｃｍ²

イ　5.9％!!
Ｐは30秒で１周する。
５秒後は、５/30＝１/６周する。
∠ＡＯＰ＝360×１/６＝60°

ＰＢを作図。

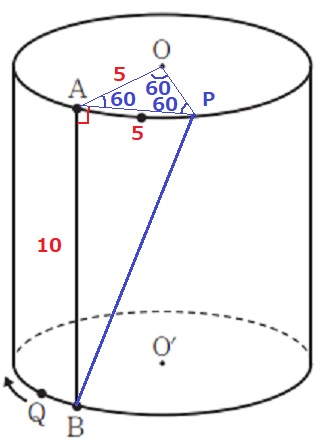
∠ＡＯＰ＝60°と半径から、△ＯＡＰは正三角形。
ＡＰ＝５ｃｍ
△ＡＢＰで三平方。
ＰＢ＝√（５²＋10²）＝√125＝５√５ｃｍ

ウ　0.7％!!!
ОＰ//О’Ｑが成立するときは、どんなときか？

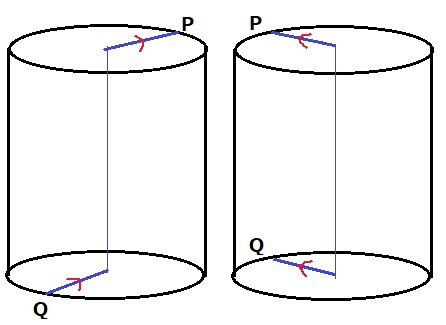
↑こんなときです。
円柱を上から見たとき、ＰがＱの反対側にくるか、重なるか。
Ｐは１周30秒、Ｑは１周45秒。
１周の長さを、30と45の最小公倍数である【90】とする。
１秒あたり、Ｐは【３】、Ｑは【２】進む。

円柱を上からみる。ＰとＱが同じ場所（ＡとＢ）から出発し、
ＰがＱの反対側にきたとき、２人のあいだは【45】離れている。
２人の距離は【３】＋【２】＝【５】ずつ縮まるので、
【45】÷【５】＝９秒後

そこからＰとＱが出会うのは、【45】÷【５】＝９秒後
さらに、ＰがＱの反対側にくるのは、２人の距離が【45】離れるときなので、
【45】÷【５】＝９秒後
つまり、９秒ごとにОＰ//О’Ｑとなる。
しかし、36秒後はＰが【３】×36＝【108】進むので、１周【90】を越してしまう。
よって、答えは９秒後、18秒後、27秒後。

エ　あ…17.1％！　い…9.8％!!
ＰＱの最小値は、円柱を上からみたときにＰとＱが重なったとき。
ＰＱ＝10ｃｍ

ＰＱの最大値は、ＰがＱの反対側にきたとき。

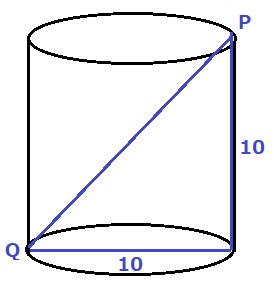
三平方から、ＰＱ＝10√２ｃｍ
10≦ＰＱ≦10√２
あ…10　い…10√２

大問４（関数）

（１）　55.1％
Ｂのｘ座標がわかっている。
ｙ＝16/ｘに代入して、Ｂ（－４、－４）
ｙ＝ａｘ²に放り込む。
－４＝（－４）²ａ
ａ＝－１/４

（２）　49.9％
Ｃのｘ座標は２。
ｙ＝16/ｘから、Ｃ（２、８）
Ｂ（－４、－４）⇒Ｃ（２、８）
右に６、上に12なので、傾きは２。
ｙ＝２ｘ＋ｂに代入して、ｂ＝４
ｙ＝２ｘ＋４

（３）　6.2％!!
ｎ≦ｘ≦４、－４≦ｙ≦０

傾きが負なので、グラフは上に凸となる。
ｘ＝４のとき、ｙ＝－４
ｙ＝０となるには、グラフが原点を通ればいい。

０≦ｘ≦４（グラフの右側）だけで、－４≦ｙ≦０となる。
このｙ変域を崩さないようにするためには、
ｘの最小値は－４≦ｘ≦０にすればいい。
ｎは整数なので、－４、－３、－２、－１、０が答え。

（４）　8.9％!!
△ＡＣＰと△ＡＣＤはＡＣを共通辺とするので、
ＡＣを底辺としたとき、△ＡＣＰの高さが５倍になればいい。

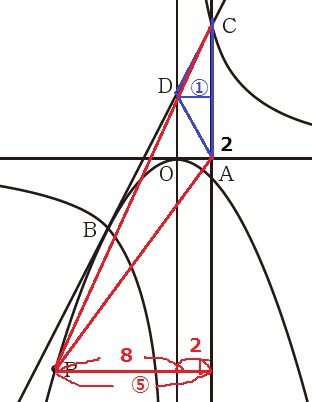
①が２ｃｍなので、⑤は10ｃｍ。
Ｐのｘ座標は－８となる。
ｙ＝－１/４ｘ²に代入。
ｙ＝－１/４×８²＝－16
Ｐ（－８、－16）

大問５（規則）

（１）　20.4％！
１ページに２人が載るので、
１組30番は、30人÷２＝15ページ
最初の２ページは学年主任や担任のページなので、
15＋２＝17ページ

３組１番の手前である、２組30番のページを求める。
１～２組まで60人の生徒がいる。
先ほどと同様に、60人÷２＋２＝32ページ
この次が３組１番だから33ページ。

（２）　3.4％!!
前問で１組30番が17ページだったので、２組は18ページから始まる。
アは偶数番号なので、２、４、６・・

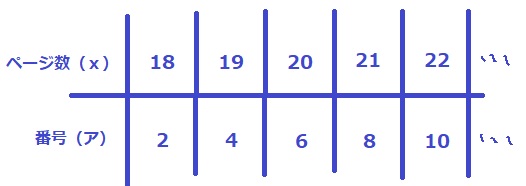
ページ数（ｘ）を用いて、番号（ア）を一般化する。
このあとで手詰まる人が多かったと思われる。

２組の前に主任や担任のページ、１組のページがあるが、
ページ下部の番号は２ずつ増えていくので、ページ数の２倍が解決の糸口になりそう。

↑こう書くと見えてくるかな？
一番上がページ数。
真ん中がページの内容（番号は偶数番号のみ）。
最初の２ページは先生、３～17ページまでが１組。
２組は18ページからはじまる。
ページ数×２との差に注目してみよう。
２組に入ると、差が34で一定である（１組最後の17ページ×２と一緒！）。
ア＝２ｘ－34

＠別解＠
別解というか、高校受験っぽく解くと一次関数を用いるのだと思われる。
ページ数をｘ軸、番号をｙ軸とする。
ｙ（ア）は２ずつ増えていくので、グラフの傾きは２。
（ｘ、ｙ）＝（18、２）を通る式の切片を求める。
２＝２×18＋ｂ
ｂ＝－34
ｙ＝２ｘ－34

（３）イ…3.9％!!、ウ…8.1％!!
積み重ねた紙を横から見る。

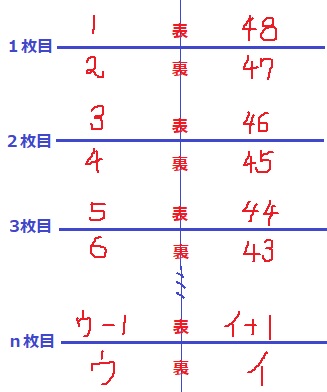
１枚目の表が１ページと48ページ。
その裏が２ページ目と47ページ。
２枚目の表が３と46、裏が４、45。
注意すべきは裏面を下にするので、イとウは左右が逆になる！
（ひっくり返して上から裏面をみると、右がイ、左がウになる）

裏面の数字だけをみる。
【ウ】
ウがわかりやすいので、先にウから。
左下の数字に注目。
２、４、６・・
ｎ枚目は２ｎ。

【イ】
47、45、43・・イ
48－１、48－３、48－５・・
１、３、５…は奇数なので２ｎ－１。
ｎ枚目は、48－（２ｎ－１）＝－２ｎ＋49

＠別解＠
どのページも左右の数字の和が49なので、
先ほどの２ｎを使い、49－２ｎ（＝－２ｎ＋49）

（４）　0.7％!!!
ａ－ｂ＝10ということは、ａ＞ｂ。
この関係が成り立つのは、前問のイ・ウのように裏面である。

ａ、ｂは２組の偶数番号で、
それぞれの番号が載っているページをＡページ、Ｂページとする。
（２）の式から、ａ＝２Ａ－34、ｂ＝２Ｂ－34
ａ－ｂ＝２Ａ－34－（２Ｂ－34）
＝２Ａ－２Ｂ＝２（Ａ－Ｂ）＝10
Ａ－Ｂ＝５
ページ数の差が５になるところを探す。

１枚の紙に４ページ分（左右と表裏）あって全部で48ページだから、
48÷４＝12枚の紙がある。
紙を開いたとき、左右ともに２組が登場するということは、
折り返し付近にあるのではないかと推測。

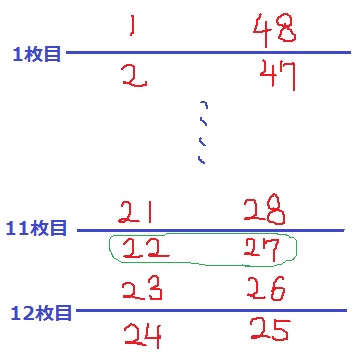
（３）と同様に、重ねた紙を横からみると、
折り返しの24ページは12枚目（一番下）の裏にくる。
（前問のウで、２ｎ＝２×12＝24が成立している）

（24、25）の組み合わせから、（－１、＋１）をして調べていくと、
11枚目の裏面で22ページと27ページの差が５になる。
よって、11枚目の裏。
公立高校入試解説ページに戻る