2020年度　京都府公立高校入試問題過去問・前期【数学】解説

問題はコチラ→ＰＤＦファイル

大問１（計算）

（１）
８×（－３/２）²－（－４²）
＝８×９/４－（－16）
＝18＋16＝34

（２）
（４ａ－３）/６－（６ａ－５）/９
＝｛３（４ａ－３）－２（６ａ－５）｝/18
＝（12ａ－９－12ａ＋10）/18
＝１/18

（３）
２/３ｘ²ｙ³÷（－１/８ｘｙ）÷４/９ｙ
＝－12ｘｙ

（４）
半径４ｃｍの円の面積が16πｃｍ²
弧の長さと中心角は比例関係。
〔16πｃｍ²で中心角360°〕なので、
６πｃｍ²の扇形の中心角は、360×６π/16π＝135°

（５）
ｘ＝５、ｙ＝－３を代入。
５ａ＋３ｂ＝23　…①
10＋３ａ＝31　…②

②より、３ａ＝21
ａ＝７
①に代入して、35＋３ｂ＝23
ｂ＝－４
ａ＝７、ｂ＝－４

（６）
ａ²＋12ａ＋35
＝（ａ＋５）（ａ＋７）　←ここで代入
＝（√30－６＋５）（√30－６＋７）
＝（√30－１）（√30＋１）　←和と差の平方
＝√30²－１²＝29

（７）
３ｘ²－８ｘ－４＝０
因数分解ができないので解の公式を適用。
ｘの係数が偶数なので、ｂ＝２ｂ’が使える。
ｘ＝（４±２√７）/３

（８）
ｘが負の範囲で、ｘが増加するとｙも増加する関数を選ぶ。
一次関数（比例）であるアイウエのなかで、アウは傾きが正。
ｘが負の領域でも右上にあがっていくので、ｘが増えればｙも増える。
放物線であるオカで、上に凸となるカが題意に適する。
ア・ウ・カ

（９）
１回目の玉を袋に戻さずに２回目の玉をとるので、
１度に袋から２個の玉を取り出すのと同じ。
全体の場合の数は、６個から２個取り出す→₆Ｃ₂＝15通り

【少なくとも１個は黒＝全体－黒を２個取る】
黒を２個を取り出す組み合わせは１通り。
よって、14通り。
14/15

大問２（データの活用）

（１）
50人の中央値（メジアン）→25番目と26番目の平均値
０以上～６未満までの合計が18人。
中央値は６以上～８未満の階級に含まれ、ア・イ・ウ・エ…と判断するのは早計。
念のため、０以上８未満の度数を確認すると18＋８＝26人となり、26番目は最大でも７冊。
25番目と26番目の平均値は7.5冊にならない。
したがって、ア・イ・ウ。

（２）
『４以上６未満の相対度数は等しい』ので、
Ｘ＝40×10/50＝８

Ｙ＋Ｚ＝40－（２＋８＋６＋４＋６）＝14
また、『８以上10未満の相対度数は３年生の方が大きい』ので、
３年生の８以上10未満の度数（Ｙ）は、40×15/50＝12人より大きい。
つまり、（Ｙ、Ｚ）＝（13、１）（14、０）のいずれか。
『３年生の最大値が16冊』だから、（Ｙ、Ｚ）＝（13、１）となる。
Ｘ＝８、Ｙ＝13、Ｚ＝１

大問３（平面図形）

（１）
△ＡＢＤ∽△ＥＡＤの証明。

証明問題としてはわかりすい。
１つは共通角。
もう１つは、二等辺三角形ＡＤＣの底角＋円周角のコンボ。
２角が等しく∽。

（２）
前問の∽を用いる。
ＢＤ：ＡＤ＝ＡＤ：ＥＤ＝12：９＝４：３
ＢＤ＝12×４/３＝16ｃｍ
ＢＥ＝16－９＝７ｃｍ

（３）

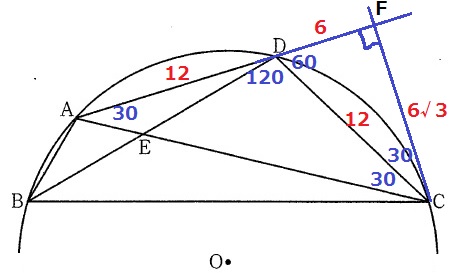
ＡＤを延長、ＣからＡＤに向けて垂線をおろした交点をＦとする。
すると、内角が30°－60°－90°の直角三角形がみつかる。
１：２：√３より、ＣＦ＝12×√３/２＝６√３
△ＡＣＦも１：２：√３の直角三角形。
ＡＣ＝６√３×２＝12√３ｃｍ

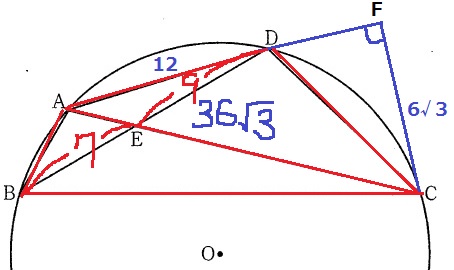
△ＡＣＤの面積…12×６√３÷２＝36√３ｃｍ²
ここで、ＤＥ：ＥＢ＝９：７を使う。
△ＡＣＤと△ＡＢＣはＡＣを共有しており、
ＡＣを底辺とすると、高さの比はＤＥ：ＥＢ＝９：７となる。
面積比も△ＡＣＤ：△ＡＢＣ＝９：７
△ＡＢＣの面積…36√３×７/９＝28√３ｃｍ²

大問４（関数）

（１）
ｙ＝－１/２ｘ＋７より、Ｂ（６、４）
これをｙ＝ａｘ²に放り込む。
４＝36ａ
ａ＝１/９

ｙ＝－１/２ｘ＋７から同様に、Ｃ（２、６）
ＡＣ：ＣＤ＝５：４と使う。
ＣとＤ（Ｂ）のｘ座標の差がちょうど４なので、ＡとＣのｘ座標の差は５。
Ａのｘ座標…２－５＝－３

（２）
ｙ＝１/９ｘ²より、Ａ（－３、１）
Ａ（－３、１）→Ｃ（２、６）
右に５、上に５なので傾きは１。
Ａ座標から右に３、上に３いくと切片は４。
ｙ＝ｘ＋４

（３）
問題集では定番なので方針は立てやすい。
丁寧に処理できるかどうか。

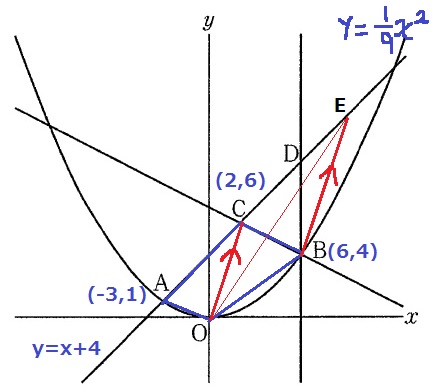
ＯＣ//ＢＥをとらえる。
等積変形より△ＯＣＢ＝△ＯＣＥとなり、
四角形ＯＢＣＡと三角形ＯＥＡが等積となる。
ＯＣ；ｙ＝３ｘ
ＢＥ；傾きが３で（６、４）を通る式。
４＝３×６＋ｂ
ｂ＝－14
ｙ＝３ｘ－14

Ｅはｙ＝ｘ＋４とｙ＝３ｘ－14の交点。
ｘ＋４＝３ｘ－14
ｘ＝９
ｙ＝９＋４＝13
Ｅ（９、13）

大問５（空間図形）

（１）

ＢＰ＝ＤＱ＝３ｃｍから、ＰとＱは同じ高さにある。
そこで、ＰとＱを通る断面で考えてみよう。
ＰＱは１辺が６ｃｍの正方形の対角線→６√２ｃｍ

（２）

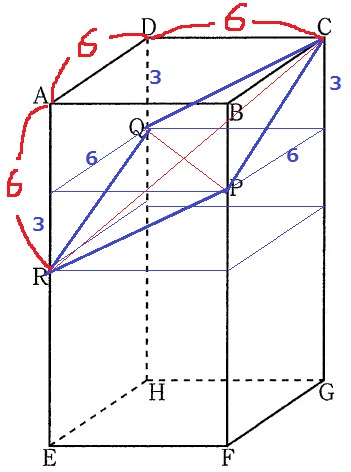
四角形ＣＱＲＰに着目。
この４辺は直方体の側面にある、３ｃｍと６ｃｍを２辺とする直角三角形の斜辺。
すなわち、ＣＱ＝ＱＲ＝ＲＰ＝ＰＣとなり、四角形ＣＱＲＰは菱形。
〔菱形の面積＝対角線×対角線÷２〕
ＰＱはわかっているので、ＣＲの長さを求めにいく。
ＣＲは１辺が６ｃｍの立方体の対角線。
ＣＲ＝√（６²＋６²＋６²）＝√108＝６√３ｃｍ
よって、四角形ＣＱＲＰの面積は、６√２×６√３÷２＝18√６ｃｍ²

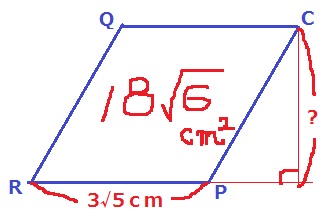
ＣＱとＰＲの距離は、ＲＰを底辺としたときの高さにあたる。
菱形の面積は、底辺ＲＰ×高さ？＝18√６ｃｍ²

ＲＰ＝ＱＣ
→ＱＣの長さは立体図における△ＤＱＣで三平方。
ＲＰ＝√（６²＋３²）＝３√５ｃｍ
よって、18√６÷３√５＝６√30/５ｃｍ

（３）

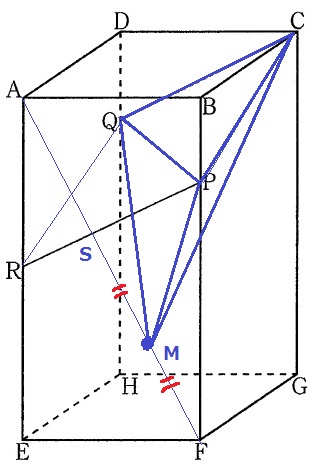
ココを求める。
変な場所にあるときは、どこかに配置転換することを考える。

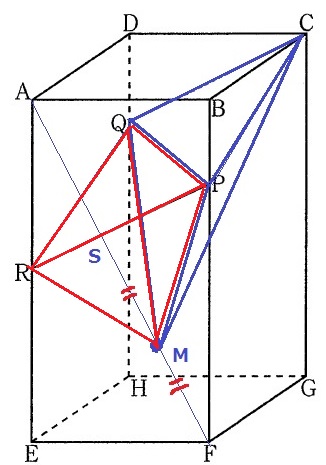
ＰＱは菱形ＣＱＲＰの対角線である。
菱形は対角線で二等分されるので、△ＣＰＱと△ＲＰＱの面積が等しい。
この２つの三角形を底面として三角錘Ｍ－ＣＰＱと三角錘Ｍ－ＲＰＱをとらえると、
面積が等しい２つの底面は同一平面上にあるので、面ＣＱＲＰからＭまでの錘の高さが共通し、
Ｍ－ＣＰＱとＭ－ＲＰＱの体積が等しい。
言い換えれば、求積すべき立体はＭ－ＲＰＱでもいい。

なぜ、Ｍ－ＲＰＱに切り替えるとうれしいのかというと、
３点Ｐ・Ｒ・Ｍが面ＡＥＦＢ上にあり、△ＰＲＭを底面とすると高さがＡＤ、
すなわち、正方形の１辺である６ｃｍと判明しているので体積が求めやすいから。
△ＰＲＭの面積さえわかれば決着がつく。

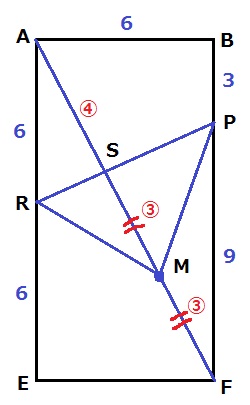
しかし、ここまでありつけても△ＰＲＭの面積が求めにくい(´ﾟдﾟ｀)
ＳＭ＝ＭＦを活用できないか。

ＲＦに補助線。
△ＰＲＦの面積は、９×６÷２＝27ｃｍ²
ＰＲを底辺とすると、△ＰＲＦの高さの半分が△ＰＲＭなので、
△ＰＲＭの面積は、27÷２＝13.5ｃｍ²
求積すべき立体の体積は、13.5×６÷３＝27ｃｍ³

大問６（規則）

（１）
６の箱に玉が入るのは、６の倍数の回数。
玉が３個…６×３＝18回目
玉が４個…６×４＝24回目
ア…18、イ…24

（２）
ａ回目に３の箱にｂ個の玉。
３の倍数ごとに３の箱へ玉が１個はいる。
ｂ個になるには、３×ｂ回の操作をしたことになる。
つまり、ａ＝３ｂ　…①

後半も同様。
『そこから（３の箱がｂ個になったときから）85回目に８の箱にｂ個の玉』
ａ＋85＝８ｂ　…②

①を②に代入。
３ｂ＋85＝８ｂ
ｂ＝17
①より、ａ＝17×３＝51
ａ＝51、ｂ＝17

（３）
整理しながら淡々と処理していく。
箱４の赤…267÷４＝66…→66個
箱９の赤…267÷９＝29…→29個

箱９に黄色の玉が66個追加されると、玉の合計は29＋66＝95個
そのときの操作の回数は、９×95＝855回目
855回目の箱４に入っている玉の合計は、855÷４＝213…→213個
赤が66個なので、４の箱の黄色の数は、213－66＝147個
公立高校入試解説ページに戻る