平均61.1点(前年比;-1.2点)

問題はこちら→東京都教育委員会
2020年度・分割後期(数学)の解説はコチラ。
大問1(小問集合)-74.7%
(1) 78.0%
9-8÷1/2
=9-16
=-7
(2) 93.8%
3(5a-b)-(7a-4b)
=15a-3b-7a+4b
=8a+b
(3) 76.2%
(2-√6)(1+√6)
=2+2√6-√6-6
=-4+√6
(4) 93.2%
9x+4=5(x+8)
9x+4=5x+40
4x=36
x=9
(5) 93.1%
7x-3y=6 …①
x+y=8 …②
以下、加減法。
②より、y=8-x …③
①に代入。7x-3(8-x)=6
10x=30
x=3
③より、y=8-3=5
x=3、y=5
(6) 57.3%
3x2+9x+5=0
解の公式を適用して、
x=(-9±√21)/6
(7) 77.2%
5以上15未満までの度数の合計は、12+14=26
26/40=65/100=65%
あ…6、い…5
*相対度数ではなく百分率。
(8) 37.3%
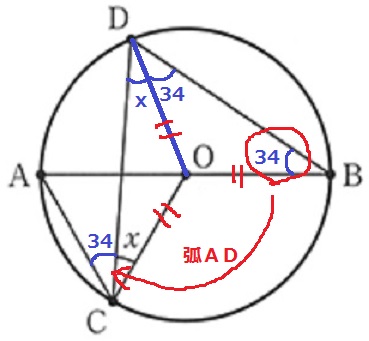
ODに補助線。
△BODと△CODは半径より、ともに二等辺。
∠BDC=x+34°
また、弧ADに対する円周角から、∠ACD=34°
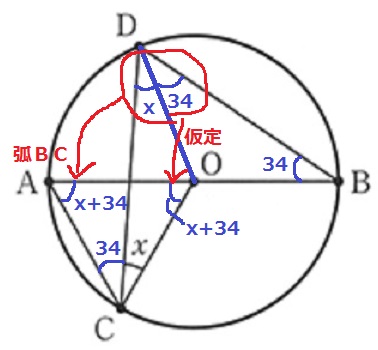
弧BCに対する円周角より、∠OAC=x+34°
問題文の仮定から、∠AOC=∠BDC=x+34°
すると、△AOCの内角がどれもx+34°となる。
つまり、正三角形なので、x+34=60
x=26°
う…2、え…6
(9) 66.0%
作図問題。
AP=BP
→PはAとBから等距離にある。
→ABの垂直二等分線
これと辺ACとの交点が点Pとなる。
大問2(式の証明)-44.5%
(1) 62.7%
X-Y
=a×a×π×h-b×b×π×h
=π(a2-b2)h
→ア
*分配法則を心がけよう。
(2) 26.3%!(無答-57.6%)
1個ずつ順を追って正確に処理する。
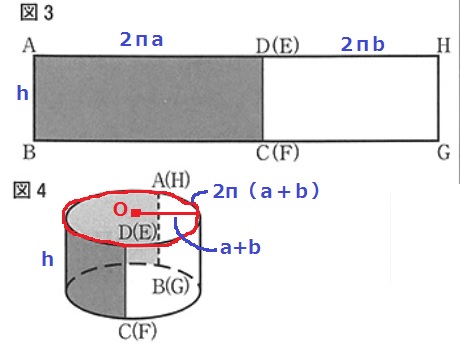
まず、図3の長方形の横の長さAHを調べる。
ADの長さ…半径aの円周(2πa)
EHの長さ…半径bの円周(2πb)
AHの長さ…2πa+2πb=2π(a+b)
これが図4の赤線の円周に匹敵するので半径はa+b
図4の体積Z…π(a+b)2h
XとYの体積の和であるWは、前問の答えを利用し、
-を+に置き換えればいい。W…π(a2+b2)h
Z-W
=π(a+b)2h-π(a2+b2)h
=π{(a+b)2-(a2+b2)}h
=π(a2+2ab+b2-a2-b2)h
=2πabh
大問3(関数)-53.6%
(1) 74.2%
言い換えれば、y=1/4x2のグラフにおいて、
xの範囲が-8≦x≦2のときのyの範囲を求める。
下に凸のグラフであり、原点を通過する点に注意!
x=0のとき、最小値y=0
x=-8のとき、最大値y=1/4×(-8)2=16
0≦y≦16
①…ウ、②…キ
(2) 69.0%
Aのy座標…y=1/4×42=4
Pのy座標…y=1/4×(-6)2=9
P(-6、9)→A(4、4)
右に10、下に5だから、傾きは-5/10=-1/2
y=-1/2x+bの式に(4、4)を代入する。
4=-1/2×4+b
b=6
y=-1/2x+6
③…エ、④…イ
(3) 17.4%!(無答-43.2%)

Pのx座標をtとする。
△AOQの面積…4×t÷2=2t
四角形OAPBはABで分割しよう。
△AOBの面積…8×4÷2=16
△ABPの底辺は8、高さは1/4t2-4
△ABPの面積…8×(1/4t2-4)÷2=t2-16
四角形OAPBの面積…16+(t2-16)=t2
四角形OAPBは△AOQの4倍なので、
t2=2t×4=8t
t2-8t=t(t-8)=0
Pのx座標は4より大きいので、t>4、t=8
Pのx座標は8となる。
大問4(平面図形)-45.6%
(1) 64.6%
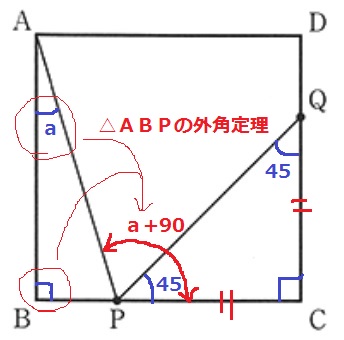
△CPQは直角二等辺三角形→∠QPC=45°
△ABPの外角定理より、∠APC=a+90°
∠APQ=(a+90)-45=a+45°
ウ
(2)① 65.7%
△ABP≡△EDQの証明。

●は正方形の1辺。
正方形の内角&外角から、∠ABP=∠EDQ=90°
CP=CQ=×とすると、
●-×=○より、BP=DQ=○
2辺の長さと間の角が等しいので合同。
② 6.6%!!(無答-24.0%)
AB=4、BP=3から、△ABPは3:4:5の直角三角形。
AP=5
前問の合同より、QE=5

△ABPの内角を●-×-90°として角度を調査する。
∠RAE=90-×=●
前問の合同より、∠AER=∠PAB=×
△AERの残りの角∠ARE=90°となり、
△AERの内角が●-×-90°→3:4:5の直角三角形。
ER=8×4/5=32/5
QR=32/5-5=7/5
EQ:QR=5:7/5=25:7
お…2、か…5、き…7
@@@
昨年の和歌山(大問5)で同じ図形が出ました。

正方形ABCDの1辺の長さが6cmのとき、四角形IECGの面積はいくつでしょうか?
△AIHが1:2:√3の直角三角形であるとわかれば、サクっと解けちゃいます。
大問5(空間図形)-20.4%
(1) 38.3%(無答-16.1%)

辺QPは面QEPB上にあり、面QEPBは辺DQと点Qで垂直に交わるので、
∠DQP=90°
△QEPで三平方→QP=6√5cm
△DPQの面積は、8×6√5÷2=24√5cm2
く…2、け…4、こ…5
(2) 2.4%!!(無答-40.7%)
△ADQで三平方→DQ=4√5
QR=12なので、四角形DQRH=4√5×12=48√5cm2
これを底面としたときの高ささえわかればいい。
立体を上から眺めてみよう。

CP:PF=3:5より、
上からみたときのPの位置はCP=3cm、PB=5cm
PからDQに向けて垂線をひき、交点をSとする。
SPの長さが知りたいところ。
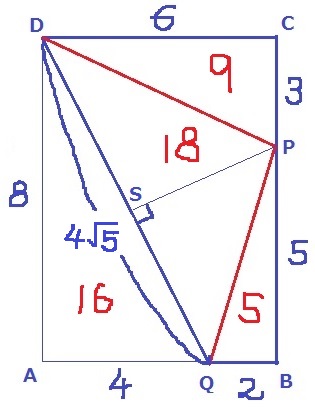
長方形から周りの3つの三角形をひく。
△DPQ=6×8-(8×4÷2+2×5÷2+6×3÷2)=18cm2
SP=18×2÷4√5=9√5/5cm
立体P-DQRHの体積は、48√5×9√5/5÷3=144cm3
さ…1、し…4、す…4
@別解@
YAさんから素晴らしい解法を頂きました。
三角形の高さについてです。

Pの真上をS、SからDQに垂線をひき、交点をTとします。
さらに、DQとCBを延長した交点をUとすると、
△ADQ∽△BUQより、BU=2×1/2=4cm
△ADQ∽△TUS(2角相等)より、
SU:ST=QD:QA=4√5:4=√5:1
ST=9×1/√5=9√5/5cmと求めることができます。
@別解2@
△DPQの求積についてです。
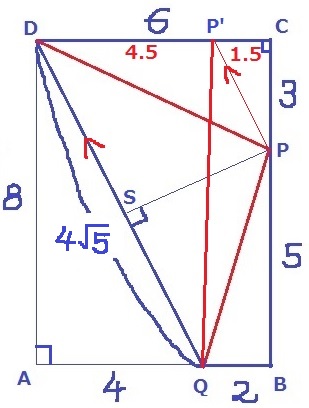
Pを通るDQに平行な線をひき、CDとの交点をP’とします。
△ADQ∽△CPP’より、AQ:AD=CP’:CP=1:2
CP’=3÷2=1.5
DP’=6-1.5=4.5
△DP’Q=4.5×8÷2=18cm2
たいして時間は変わりませんが…ちょっとした小技です。
@別解3@
うえの平行線を使います。
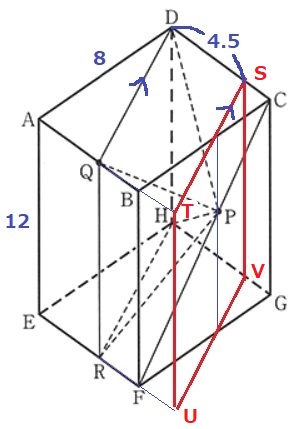
面DQRHに平行な面STUVを作成。
点Pがこの面上にあれば、等積変形と同じで立体P-DQRHの体積が同じになる。
四角形DQRHの面積がわからなくても、
P-DQRHの体積は四角柱DQTS-HRUVの3分の1である。
(錘は柱の3分の1であり、柱の体積は四角形DQTSを底面にとらえて計算する)
4.5×8×12÷3=144cm3
●講評●
平均はちょっと下がったが、80点以上の高得点者が2倍超も増加。
以下、公式の誤答分析を参照。
大問1
基礎的な計算問題は正答率が高い。凡ミス注意!
(6)解の公式は6割弱。誤答では変なふうに約分した(-3±√21)/2が多かった。
(8)弧ADに対する円周角ABDと等角だと誤解して34度が多かった。
とりあえず円がでたら、半径の補助線→二等辺と円周角の定理を疑う。
泥臭い方法でも全然構わないのでトライしよう。
大問2
(2)『四角形ABGHを側面とする円柱の底面の半径が(a+b)cmであることを、
根拠に基づいて示すことができなかったり、説明の見通しを立てられてなかったりした』
文字式の変形処理は慣れが必要。他の都道府県の生徒もチャレンジしてほしい。
大問3
(3)『条件を満たす点の座標を文字を用いた式で表し、その文字を用いて四角形OAPBの面積と
△AOQの面積の関係を表し、処理することができなかった』
計算処理はスッキリしていた。複雑な形は切断するのも手。
大問4
(1)外角定理を意識すれば、もうちょい正答率が上がるかも。
(2)②『与えられた図から解答を導くために必要となる相似な図形を見出すなどして、
線分EQと線分QRの比を考察する見通しを立てることや、処理することができなかった』
1コ目の鬼問。まず、△ABPの3:4:5に気づきたい。
直角三角形は残りの2角の和が90°ゆえ、相似図形が見つかりやすい。
大問5
(1)もうちょい正解したい。
(2)『直方体の中にできる立体の高さを正しく捉えることや、
三平方の定理などを用いて高さを求めることができなかった』
2コ目の鬼問。底面はDQRHとわかるが、錘の高さはどの方面から見た図で捉えるか。
実際に四角錘の高さを描き、平行移動させてどこかの面に写すとわかりやすい。
来年はコロナ禍の影響で三平方と標本調査が出題範囲から外されるそうです。
@2020年度(都立)@
数学(分割後期) 社会…平均57.0点 理科…平均53.4点 英語…平均54.7点
その他は下記リンクの目次からどうぞです。



コメント