2017年度　神奈川県公立高校入試【数学】解説

平均６３．５点

易化です。簡単な問題は手際良く処理しましょう。
大問４、５のラストが厳しいか。
問題はコチラから→ＰＤＦファイル

大問１（計算）

（ア）　97.6％
（－７）＋（－９）＝－７－９＝－１６

（イ）　95.0％
－１/３＋３/８＝１/２４

（ウ）　98.5％
３２ａ²ｂ÷４ａｂ＝８ａ

（エ）　94.1％
√７５＋１２/√３
＝５√３＋１２√３/３　←有理化
＝５√３＋４√３＝９√３

大問２（小問集合１）

（ア）　88.0％
（ｘ＋５）（ｘ＋９）－（ｘ＋６）²
＝ｘ²＋１４ｘ＋４５－（ｘ^２＋１２ｘ＋３６）←符号ミス注意
＝２ｘ－９

（イ）　90.7％
（ｘ－３）をＸに置き換えると、
Ｘ²－２Ｘ－３５＝（Ｘ－７）（Ｘ＋５）
＝{（ｘ－３）－７}{（ｘ－３）＋５}  ←Ｘを（ｘｰ３）に置き換え
＝（ｘ－１０）（ｘ＋２）

（ウ）　85.5％
解の公式を用いる。
ｘ＝（５±√３３）/４

（エ）　8.6％!!
ＡＤとＢＧを延長して交点をＩとする。
ＢＧ：ＧＩ＝△ＧＢＣ：△ＧＩＤ＝ＣＧ：ＧＤ＝２：１
ＢＦ＝③、ＦＣ＝①とするとＩＤ＝②、ＩＥ＝④となるので
ＢＨ：ＨＩ＝△ＨＢＦ：△ＨＩＥ＝ＢＦ：ＩＥ＝３：４
あとは、ＢＨＧＩ上で比をそろえればよい。
ＢＨ：ＨＧ：ＧＩ＝９：５：７　→　ＢＨ：ＨＦ＝９：５

大問３（小問集合２）

（ア）　88.8％
*変化の割合＝ｙの増加量/ｘの増加量
{－３×３^２－（－３）×１²}/（３－１）＝－２４/２＝－１２
もしくは、y=ax²でｘの値がｐからｑまで増加するときの変化の割合はa（ｑ＋ｐ）なので、
－３（３＋１）＝－１２

（イ）３　67.5％
*３割引き→７割

（ウ）２　81.3％
*２０人のメジアン→１０人目と１１人目の平均値
ケアレスミスしないように、小さい値から数字を消して確認。
１０人目は６回、７人目は７回なので、６．５

（エ）４　73.7％
*そのまま代入しない。変形してから代入。
xy=（√５＋√３）（√５－√３）＝５－３＝２
ｘ＋ｙ＝（√５＋√３）＋（√５－√３）＝２√５
ｘ²ｙ＋ｘｙ²＝ｘｙ（ｘ＋ｙ）＝２×２√５＝４√５

（オ）１　70.7％
*ｘ²－５ｘ－６＝０の解を求める。
（ｘ－６）（ｘ＋１）＝０　　ｘ＝－１、６
大きい方の解である６が他方の１つの解でもあるので、６を代入する。
６²＋６ａ－２４＝０　　６ａ＝－１２　　ａ＝－２

大問４（関数）

（ア）４　89.3％
*Ａ（２、２）→ｙ＝ａｘ²に代入する。ａ＝１/２

（イ）５　73.7％
*ＢはＡをｙ軸に対称移動した点なので、Ｂ（－２、２）
ＡＯ：ＯＣ＝２：３なので、Ｃのｘ座標は－３→Ｃ（－３、－３）
ＣからＢは右に１上に５→傾き５、代入して切片は１２、ｙ＝５ｘ＋１２

（ウ）３　31.5％！
*やや難。とりあえず、ＤとＥの座標を求めてみる。
Ｄ：①と②の交点から、Ｄ（１、１）
Ｅ：②上でｘ座標が３だから、Ｅ（３、－１）
三角形の二等分といえば等積変形を用いるのが定石だが、
今回は面積比で対処した方がやりやすい。

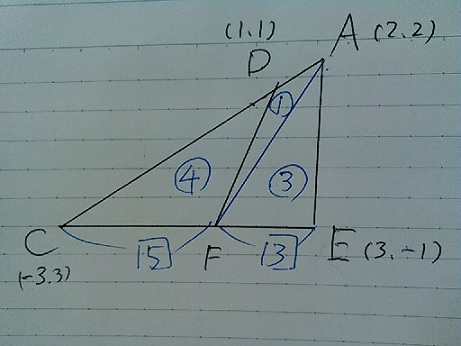
ＣＤ：ＤＡ＝４：１
ＡＦに補助線。△ＤＣＦ＝④、△ＡＤF＝①
△ＤＣＦが△ＡＣＥの半分だから、四角形ＡＤＦＥ＝④、△ＡＦＥ＝③
ということは、ＣＦ：ＦＥ＝△ＡＣＦ：△ＡＦＥ＝５：３。
ＣＥのｘ座標の距離は６離れているので、ＣＦ＝６×５/８＝１５/４
Ｆのｘ座標はCのｘ座標から＋１５/４。－３＋１５/４＝３/４

大問５（確率）

問題文が長いのでルールを正確に理解することが大事！
大小２個のサイコロを転がし、出目の約数を裏返す。
あらかじめ、出目と裏返す石の関係をまとめておく。
（出目）　（裏返す石）
１　　→　１
２　　→　１、２
３　　→　１、３
４　　→　１、２、４
５　　→　１、５
６　　→　１、２、３、６

（ア）３　72.5％
*全ての石が白→大と小の出目が同じ。６通りだから６/３６＝１/６

（イ）５　25.1％！
*大変。パターンが意外とあるので、丁寧に調査するしかない。
１は表であろうが裏であろうが積は変わらないので考慮しない。
６０を素因数分解すると２×２×３×５
・６０を作る→（２、５、６）から（３、４、５）
（２５６）→３と４が黒→しかし、２回の操作では不可能
（３４５）→２と６が黒→３と６を出す→２通り
・１２０を作る→（４、５、６）（２、３、４、５）
（４５６）→２と３が黒→２と３を出す→２通り
（２３４５）→６が黒→しかし、不可能
・１８０を作る→（２、３、５、６）
（２３５６）→４が黒→２と４を出す→２通り
・２４０を作る→（２、４、５、６）
（２４５６）→３が黒→１と３を出す→２通り
・３００を作る→無
・３６０を作る→（３、４、５、６）
（３４５６）→２が黒→１と２を出す→２通り
・７２０を作る→（２、３、４、５、６）
（２３４５６）→ようは全て白で前問と同様→６通り
全部で１６通り→１６/３６＝４/９

ポイントは起点となる６０の２パターン
（２、５、６）と（３、４、５）から数字をかけていく。
数字は１～６の範囲で、同じ数字は重複できない。
１２０は６０×２で（２、５、６）→（４、５、６）
（３、４、５）→（６、４、５）
１８０は６０×３で(２、５、６）→（２、３、５、６）
（３、４、５）→３倍不可。
各々の数字を３倍すると６を超えてしまい、すでに３があるので３を増やせない。
３６０は（３、４、５、６）なので、次の６０の倍数は余っている２をかけた７２０となる。