2020年度　京都府公立高校入試過去問・中期【数学】解説

問題はコチラ→ＰＤＦファイル
2020年度京都前期（数学）の解説はコチラから。

大問１（小問集合）

（１）
５＋４×（－３²）
＝５＋４×（－９）
＝５－36＝－31

（２）
４（３ｘ＋ｙ）－６（５/６ｘ－４/３ｙ）
＝12ｘ＋４ｙ－５ｘ＋８ｙ
＝７ｘ＋12ｙ

（３）
√３×√32＋３√６
＝√３×４√２＋３√６
＝４√６＋３√６＝７√６

（４）
２ｘ＋５ｙ＝－７…①
３ｘ＋７ｙ＝－９…②

①×３－②×２
６ｘ＋15ｙ＝－21
－)６ｘ＋14ｙ＝－18
ｙ＝－３
①に代入。
２ｘ＋５×（－３）＝－７
２ｘ＝８
ｘ＝４
ｘ＝４、ｙ＝－３

（５）
ｙ＝－４/５ｘ＋４のグラフを書く。

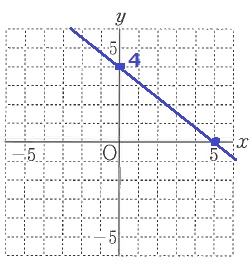
切片は（０、４）
傾きは負なので右下に向かう。
下に４、右に５で（５、０）と結ぶ。

（６）
５＜√ｎ＜６
√25＜√ｎ＜√36
ｎ＝26～35なので、10個。

（７）

ＡＣとＢＤの交点をＥとする。
円周角の定理で、∠ＢＤＣ＝54°
△ＣＤＥで外角定理→∠ＤＣＥ＝73－54＝19°
直径に対する円周角は直角なので、∠ＢＣＤ＝90°
ｘ＝90－19＝71°

（８）
無作為に抽出した300個のうち、不良品は７個。
よって、７×10000/300＝700/３＝233…≒230個

大問２（確率）

ジェンガ問題。
（１）
１回目は何かを出す。その何かが一番上にきて、Ｇは下から６番目になる。
２回目でＧのある６を出せばいい→１/６

（２）
初期状態ではＥは下から５番目。
Ｅを１段下げればいい。
■１回目でＥが下がる
１回目→１～４を出す。４通り
２回目→Ｅは４段目にいるので５か６を出す。２通り
４×２＝８通り
■２回目でＥが下がる
１回目→６を出す。１通り
２回目→Ｅは５段目にいるので１～４を出す。４通り
１×４＝４通り

８＋４＝12通り
12/36＝１/３

大問３（関数）

（１）
ｙ＝１/４ｘ²に、ｘ＝２を代入。
ｙ＝１/４×２²＝１
１ｍ

後半は、ｙ＝９を代入。
１/４ｘ²＝９
ｘ²＝36
ｘ＞０より、ｘ=６
６秒

（２）
普通は求めたいＡの長さを文字に置き換えたいところだが、
長さはｙ＝１/４ｘ²のｙにあたる。
長さを文字に置き換えると、往復の時間で等式をつくることになるが、
往復の時間ｘの次数が２なので計算が厳しく、かつ比しかわかっていない。

そこで、往復の時間ｘを文字に置き換える。
Ａの往復の時間をｔ秒とする。
Ｂの往復の時間は４/５ｔ秒。

Ａの長さは、ｙ＝１/４ｘ²にｘ＝ｔを代入→１/４ｔ²
Ｂの長さは、ｘ＝４/５ｔを代入→４/25ｔ²
『Ａの長さはＢより１/４ｍ長い』から、長さで等式。
１/４ｔ²＝４/25ｔ²＋１/４
９/100ｔ²＝１/４
ｔ²＝100/36＝25/９
ｔ＞０より、ｔ=５/３
Ａの１往復の時間は５/３秒。
これをｙ＝１/４ｘ²に代入。
ｙ＝１/４×（５/３）²＝25/36ｍ
*振り子の周期は、おもりの重さではなく、振れ幅でもなく、
振り子の長さ（支点～おもりの重心までの長さ）に依存することを等時性という。

大問４（空間図形）

（１）
△ＡＢＣで三平方。
ＡＣ²＝（２√７）²＋６²＝64
ＡＣ＞０から、ＡＣ＝８ｃｍ
８÷１＝８秒

（２）

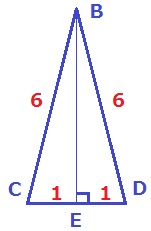
二等辺三角形ＢＣＤの縦に真っ二つ。
ＣＤとの交点をＥとして、△ＢＣＥで三平方→高さＢＥ＝√35ｃｍ
２×√35÷２＝√35ｃｍ²

錐の体積は底面積×高さ÷３。
√35×２√７÷３＝√５×√７×２√７÷３＝14√５/３ｃｍ³

（３）

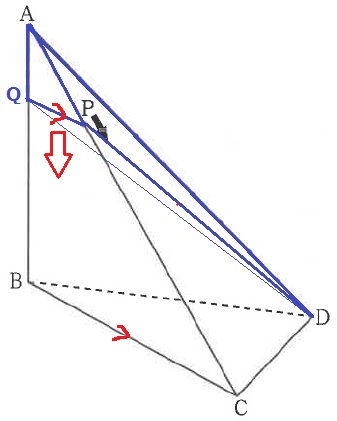
ＰＤは面ＡＣＤ上の線分。ＱＤは面ＡＢＤ上の線分。
ＢＣ//ＱＰを維持してＱＰを下に平行移動させる。
ＰがＣに着くとＰＤ＝ＣＤ、ＱがＢに着くとＱＤ＝ＢＤ
つまり、最後は三角錘Ａ－ＢＣＤになる。

△ＡＱＰを底面としたとき、△ＡＱＰと△ＡＢＣの底面積の比は、
三角錘Ｄ－ＡＱＰと三角錘Ｄ－ＡＢＣの体積比に等しい。

三角錘Ｄ－ＡＱＰ：三角錘Ｄ－ＡＢＣ
＝24√５/７：14√５/３
＝72：98
＝36：49

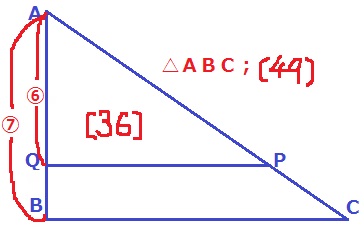
△ＡＱＰ：△ＡＢＣ＝36：49
ちょうど値が平方数！→ＡＱ：ＡＢ＝⑥：⑦
（１）より、Ｐが８秒でＣに着く＝Ｑは８秒でＢに着くので、
８×⑥/⑦＝48/７秒後

大問５（平面図形）

（１）

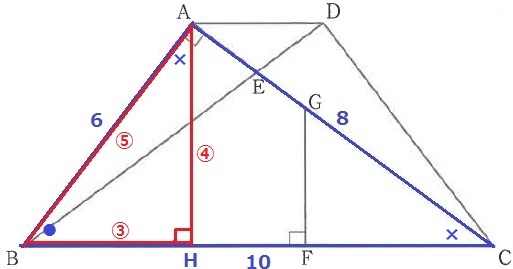
ＡＢ＝６ｃｍ、ＡＣ＝８ｃｍから、直角三角形ＡＢＣの辺の比は３：４：５。
ＡからＢＣに向けて垂線、足をＨとする。
●＋×＝90°で２角が等しく、△ＡＢＣ∽△ＨＢＡから辺の比は３：４：５。
ＡＨがＡとＢＣの距離にあたる。
ＡＨ＝６×４/５＝24/５ｃｍ

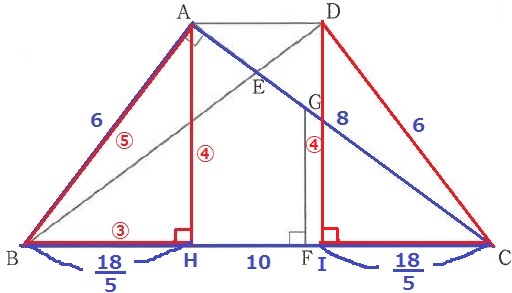
Ｄから垂線をひく。足をＩとする。
ＤＩは台形ＡＢＣＤの高さでＡＨと同じ。
ＣＤ＝６ｃｍより、斜辺と他の１辺が等しい直角三角形で△ＡＢＨ≡△ＤＣＩ
（ここから台形ＡＢＣＤは左右対称の等脚台形となる）
ＢＨ＝ＣＩ＝６×３/５＝18/５
ＡＤ＝ＨＩ＝10—18/５×２＝14/５ｃｍ

（２）

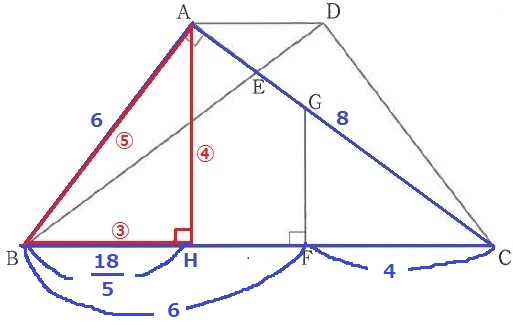
ＢＣ＝10ｃｍをＢＦ：ＦＣ＝３：２で按分。
ＢＦ＝６ｃｍ、ＦＣ＝４ｃｍ
ＨＦ＝６－18/５＝12/５ｃｍ
△ＡＣＨ∽△ＧＣＦで、ＡＧ：ＧＣ＝ＨＦ：ＦＣ
＝12/５：４＝12：20＝３：５

（３）
今までに出てきた数値を使う。

ＡＨ＝24/５ｃｍ、ＡＤ＝14/５ｃｍ
ここから△ＡＣＤの面積がでる。
さらに、ＡＧ：ＧＣ＝３：５から、△ＡＤＧと△ＧＤＣの面積比は３：５。
△ＧＤＣの面積が求められる。

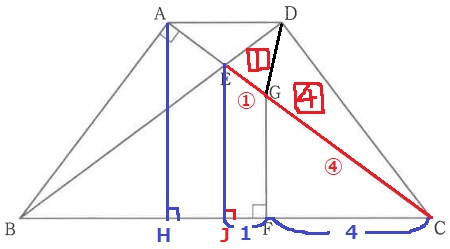
台形ＡＢＣＤは等脚台形で、対角線ＡＣとＢＤの交点Ｅからおろした垂線の足をＪとすると、
ＪはＢＣの中点である。（左右対称だから）
ＪＣ＝10÷２＝５ｃｍ
ＪＦ＝５－４＝１ｃｍ
△ＥＣＪ∽△ＧＣＦより、ＥＧ：ＧＣ＝ＪＦ：ＦＣ＝１：４
△ＥＤＧの面積を【１】とすると、△ＧＤＣの面積は【４】
以上をつなげる。△ＡＣＤ⇒△ＧＤＣ⇒△ＥＤＧ。
14/５×24/５×１/２×５/８×１/４＝21/20ｃｍ²

大問６（規則）

（１）

奇数に注目すると、タイルの枚数がちょうど平方数。
７番目は４×４＝16枚
１枚のタイルは１ｃｍ²なので16ｃｍ²
*１は１番目の奇数だから１×１枚。
３は２番目（＝（３＋１）÷２）の奇数だから２×２枚
５は３番目（＝（５＋１）÷２）の奇数だから３×３枚
７は４番目（＝（７＋１）÷２）の奇数だから４×４枚

偶数は長方形で考える。

２は１番目（＝２÷２）の偶数だから１枚
４は２番目（＝４÷２）の偶数だから１＋２＝３枚
６は３番目（＝６÷２）の偶数だから１＋２＋３＝６枚
16は16÷２＝８番目の偶数だから、１～８の総和。
これは長方形の数なので、タイルの枚数は２倍すること。
（１＋８）÷２×８×２＝72ｃｍ²

＠別解＠
先ほどの奇数から解くこともできる。
15は（15＋１）÷２＝８番目の奇数なので、８×８＝64枚
奇数から偶数の変換をみると、
１番目→２番目；１＋１＝２枚
３番目→４番目；４＋２＝６枚
５番目→６番目；９＋３＝12枚…
奇数の〇番目を足す。
15は８番目の奇数だから、64＋８＝72枚（72ｃｍ²）

（２）
今までのおさらいだが混乱しやすい。
ｎは偶数なので偶数のルールを適用。
ｎはｎ÷２＝ｎ/２番目の偶数。
１～ｎ/２までの総和を求める。（あくまで長方形の数なので最後は２倍！）
（１＋ｎ/２）×ｎ/２÷２×２＝ｎ²/４＋ｎ/２…ｎ番目のタイルの枚数

ｎが偶数なので２ｎ＋１は奇数。奇数のルールを適用。
２ｎ＋１は（２ｎ＋１＋１）÷２＝ｎ＋１番目の奇数。
（ｎ＋１）²＝ｎ²＋２ｎ＋１…２ｎ＋１番目のタイルの枚数

差の331で等式。
ｎ²＋２ｎ＋１－331＝ｎ²/４＋ｎ/２　←両辺を×４
４ｎ²＋８ｎ－1320＝ｎ²＋２ｎ
３ｎ²＋６ｎ－1320＝０　←両辺を÷３
ｎ²＋２ｎ－440＝０
（ｎ＋22）（ｎ－20）＝０
ｎ＞０より、ｎ＝20

＠別解＠
〇番目の奇数さえわかれば〇の平方数でタイルの枚数がでるので、
奇数ルールでゴリ押しすることもできる。

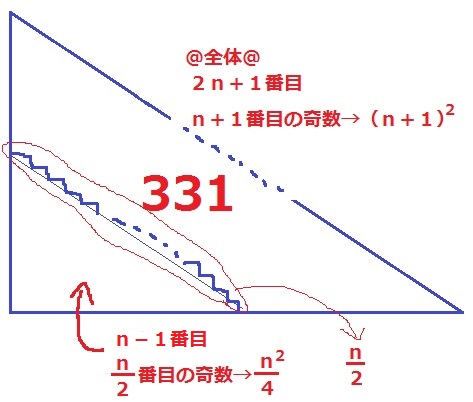
全体は２ｎ＋１番目でこれはｎ＋１番目の奇数だから、（ｎ＋１）²枚とすぐでる。
問題はｎが偶数で、こちらは直角三角形ではなく階段状であること…。
ｎの１個手前のｎ－１が奇数。
ｎ－１は（ｎ－１＋１）÷２＝ｎ/２番目の奇数だから、（ｎ/２）²＝ｎ²/４枚
奇数→偶数の変換では〇番目の奇数の〇を足すので、
ｎ²/４＋ｎ/２と（ｎ＋１）²の差が331となる。
（ｎ＋１）²－（ｎ²/４＋ｎ/２）＝331
これを解くと、ｎ＝20になる。
公立高校入試解説ページに戻る