平均55.9点(前年比;+2.3点)
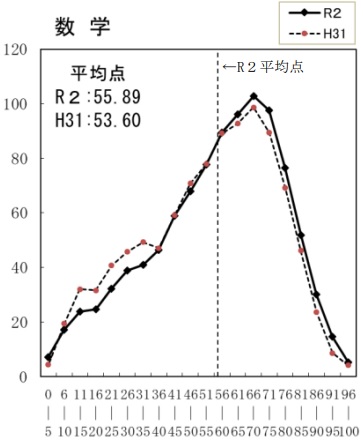
100点の人数-15名、0点の人数-8名
問題はこちら→東進ハイスクールさん(解答)
大問1(小問集合)
(1)
3-(-5)
=3+5
=8
(2)
-42
=-(4×4)
=-16
ウ
*(-4)2=(-4)×(-4)=16
(3)
2(x-1)=-6
2x-2=-6
2x=-4
x=-2
(4)
√75-9/√3
=5√3-3√3
=2√3
(5)
2nは、2で割り切れるので必ず偶数。
2n+1は、偶数である2nに+1をするので奇数。
同様に、2n+3も奇数。
ウ・エ
(6)
ヒント付きでありがたい。
698×702
=(700-2)(700+2)
=7002-22
=490000-4
=489996
あ…700、い…2
(7)
反比例は積xyが常に比例定数a。
a=xy=1×(-16)=-16
う=-16÷3=-16/3
(8)
x=0のとき、最小値y=0
x=2のとき、最大値y=8
0≦y≦8
→ア
(9)
ご丁寧に樹形図が提供されている。
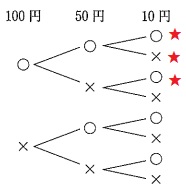
110円以上は3通り。
3/8
(10)
対称の軸を作成。
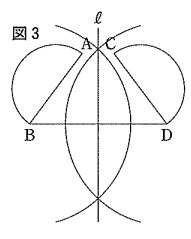
BとDが対応する点なので、BDの垂直二等分線を引けばいい。
必ず『ℓ』の記号を書くこと!
ACの垂直二等分線でもいい。
(11)①
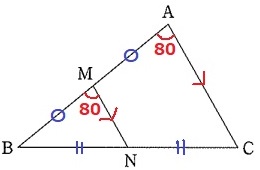
中点連結定理から、MN//AC
同位角により、∠BMN=80°
②
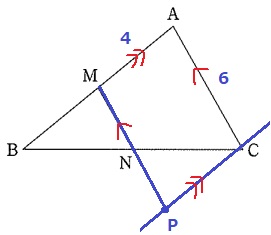
AM//CPで、四角形AMPCは2組の対辺が平行で平行四辺形。
周の長さは、(4+6)×2=20cm
大問2(小問集合2)
(1)①
高校生の最頻値(モード)を求める。
2時間以上3時間未満
②
340÷1500=0.226…≒0.23
③
解答では理由も述べる。
相対度数を計算して比較すればいい。
1時間2時間未満の階級において、高校生の相対度数は0.23
中学生の相対度数は、262÷1000=0.262≒0.26
0.26>0.23より、中学生の方が割合が大きい。(ア)
(2)①
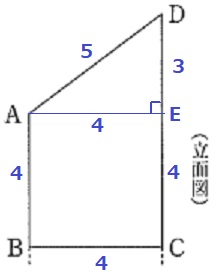
Aを通るBCに平行な線分をひき、CDとの交点をEとする。
四角形ABCEは1辺4cmの正方形。
△ADEは3:4:5の直角三角形→DE=3cm
CD=7cm
②
切断円柱は同じものを上にくっつける。
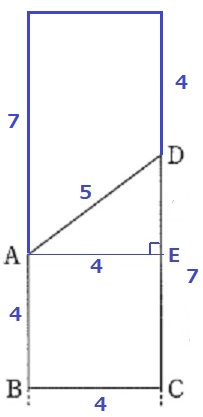
立体Pの体積は、高さ11cmの円柱の半分の体積となる。
2×2×π×11÷2=22πcm3
@余談@
最も高い7cmと最も低い4cmの高さの平均と考えてもいい。
立体Pを高さが(7+4)÷2=11/2cmの円柱とみなす。
切断系は高さの平均を疑おう。
(3)①
塵劫記の俵杉算が登場した。
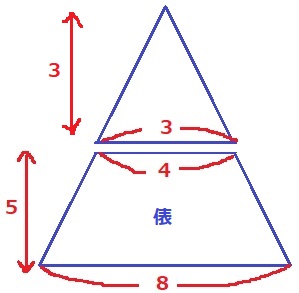
俵の上の列が4個、下の列が8個。
1辺3個の正三角形が上にあるので、俵の段数は8-3=5段
(正解例↓)
(4+8)×5÷2
12×5÷2
②
過程も記述する。
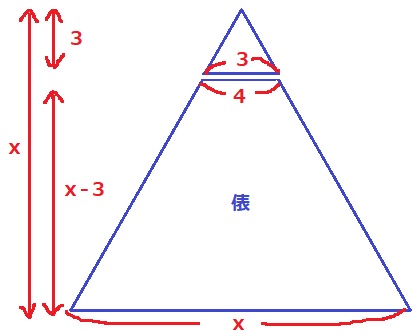
俵の最上段が4個、最下段がx個。
段数はx-3個。
あとは公式にあてはめるだけ。
{(x+4)(x-3)}÷2=60
(x+4)(x-3)=120
x2+x-132
=(x+12)(x-11)=0
x>0より、x=11
11個
@余談@
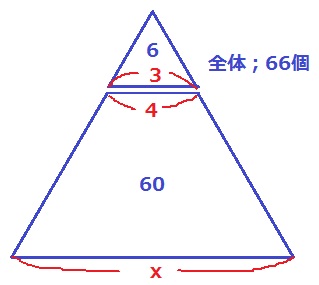
本問は方程式を記述しなければならないが、
そうでなければ、上の3段の6個を足して全体を66個にすると、
1+2+3…+11=66なのでxは11段目→x=11とわかる。
大問3(数量変化)
Ⅰ(1)
A店とB店の代金が同じになるところ。
→2つのグラフの交点Q
イ
(2)
Qはリボンの長さが50cm。
30cmではA店の方が安い。
A店;y=5x
y=5×30=150円
B店は70cmまで250円で一定。
250-150=100円安いことになる。
A店・100円
(3)
B店(x>70)のグラフの式を求める。
R(70、250)
これをy=ax-170に当てはめ、傾きaを求める。
250=70a-170
70a=420
a=6
6
(4)①
リボンの長さが50cmを超えるとB店の方が安くなるが、
70cmを超えるとB店の単価が高くなるので、再びB店が高くなるときがある。
これもグラフの交点を求めればいい。
(解答例)
y=5xとy=6x-170の連立方程式を解く。
*留意事項では「連立方程式を解く」という内容が書かれているものを評価の対象とするとある。
『y=5xとy=6x-170のグラフの交点を求める』でも良いと思う。
②
先ほどの連立を解く。
5x=6x-170
x=170
Ⅱ(1)
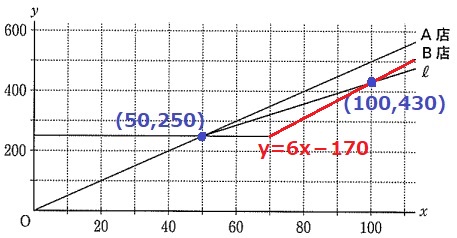
B店(x>70)のグラフであるy=6x-170において、
x=100のとき、y=6×100-170=430
直線ℓは(50、250)と(100、430)を通る。
右に50、上に180なので、傾きは180/50=18/5

100cm未満より100cm以上を買う客が多いので、
100cm以上をB店より安くしたい。
傾きが18/5(3・3/5)のとき、100cmの代金がB店と並ぶので、
これより傾きが小さければA店の方が安くなる。
かつ、売り上げが伸びる値段(整数値)を答えるので、1cmあたり3円にすればいい。
う…18/5、え…3
(2)
企画案1では、リボンが長くなるほど割引前と後のグラフの開きがどんどん大きくなる。
つまり、割引前と比べてリボンを長く買われるほど利益率が減少してしまう。

割引前の傾き5と平行にすれば、割引前のグラフとの差に開きが生まれない。
?cmまでは200円で一定。?から傾き5となり、(100、430)を通過するグラフとなる。
x>?のときのグラフの式を求める。
430=100×5+b
b=-70
y=5x-70
これにy=200を代入。
200=5x-70
x=54
よって、54cm。
@別解@
中学受験の算数的解法です。

Aは傾き5、Bは傾き6。
(100、430)の点からx座標で30後退すると、y座標は(差の1)×30=30の差がでる。
ということは、A店におけるx=70のとき、yの値は250+30=280

赤い直角三角形に注目。高さは280-200=80
底辺の横の長さは、高さ÷傾き=80÷5=16
よって、?=70-16=54cm
大問4(平面図形)
Ⅰ(1)
∠PAQ=∠RASの証明。
誘導に従い、空欄を埋める。
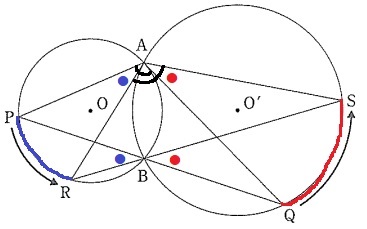
弧PRに対する円周角から、∠PAR=∠PBR(●)
弧QSに対する円周角から、∠QAS=∠QBS(●)
対頂角で、∠PBR=∠QBS
つまり、●と●はすべて等しい→∠PAR=∠QAS
あいだにある共通角RAQを足して、
∠PAR+∠RAQ=∠QAS+∠RAQ
したがって、∠PAQ=∠RAS
あ…弧QS、い…∠RAQ
(2)
今度は△PAQ∽△RASから、∠PAQ=∠RASを証明する。
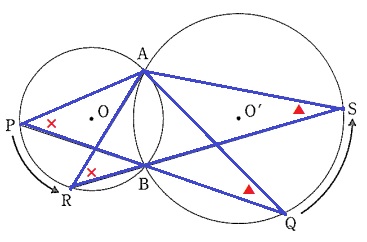
相似の証明は先ほどと同じ。円周角の定理を使う。
ただ、どちらも弧ABに対する円周角なので、
どちらの円の弧であるか明確に書いておこう。
円Oの弧ABに対する円周角は等しい。
∠APQ=∠ARS(×)
円O’の弧ABに対する円周角は等しい。
∠AQP=∠ASR(▲)
2角が等しく、△PAQ∽△RAS
相似図形は対応する角が等しいから、∠PAQ=∠RAS
*最後は証明したい等角でフィニッシュ。
(3)
対応する辺を選ぶ。
△PAQ←→△RAS
AP←→AR
AQ←→AS
イ
Ⅱ(1)
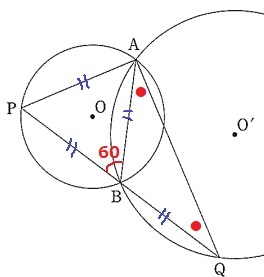
△ABPは正三角形、△ABQは二等辺三角形。
△ABQの外角定理より、●+●=60°
∠BAQ=60÷2=30°
(2)
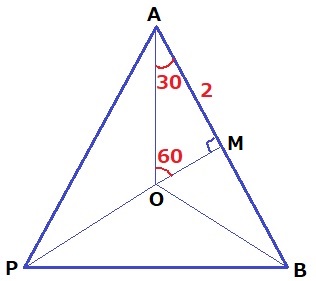
△ABPは1辺4cmの正三角形。
ABの中点をMとする。
△AMOの内角は30°-60°-90°で、1:2:√3の直角三角形。
円Oの半径であるAOは、2×2/√3=4√3/3cm
(3)
センスが問われると思う。
△ATUの面積が最大となるとき、Tはどこにいるのだろう?
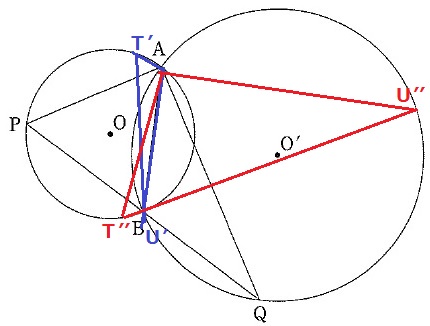
極端なケースを想像してみる。
青線はAに近いT’、赤線はBに近いT”
Bに近い△AT”U”の方が面積が大きい。
TはAを含まない弧PB上にあるのでは?

手がかりは、Ⅰ(2)の相似。
すなわち、PをB側に移動させても△APQ∽△ATUの相似関係は維持される。
〔最も面積の広い相似図形=対応する辺の長さが最も長い〕
辺APに対応する辺ATが最長となるのはズバリ、中心OをはさんでAとTが反対側にあるとき。
言い換えれば、ATが円Oの直径であるとき。

半円の弧に対する円周角は直角なので、∠ABT=90°
∠ABU=90°となり、AUは円O’の直径にあたる。
辺AQに対応する辺AUが最長となるのは、AUが円O’の直径であるときなので、
このときの△ATUが最も面積が大きいと断定できる。
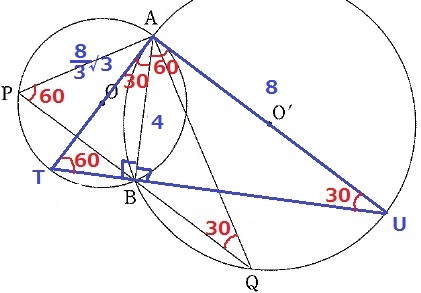
相似の証明で示したように、円周角定理から∠ATB=60°、∠AUB=30°
△ABTも△AUBも内角が30°-60°-90°の直角三角形。
∠TAU=90°
Ⅱ(2)より、円Oの半径が4√3/3cmだったので、直径AT=8√3/3cm
△ABTの辺の比は1:2:√3より、AU=4×2=8cm
よって、△ATUの面積は、8×8√3/3÷2=32√3/3cm2
(4)
△APQ∽△ATUで、AP=4cm、AT=8√3/3cmであった。
面積比は相似比の2乗。
△APQ:△ATU
=42:(8√3/3)2
=16:64/3
=48:64
=3:4
したがって、4/3倍。
●講評●
70点前後が多い。
大問1
基本問題なので、数学が苦手な子も確実に通過したい。
上位校狙いは後半の問題に時間を残すうえでも快速処理で。
(9)樹形図の提供はめったにないぞ!
大問2
(3)問題が1ページ丸々あるので、条件の読解に時間をとられないこと。
図を見てサクッと理解するのが理想。
読解力さえあれば、数学が得意でもなくてもクリアできるはず。
大問3
ここも問題文が長い。
必要な情報をテンポ良く拾って読み進められるか。
Ⅰは基本。Ⅱで差がつく。
グラフがどこを通るのか、グラフのどこが固定されるのかを見極める。
大問4
∠PAQ=∠RASを2通りの方法で証明する。
Ⅰは取っておきたい。
Ⅱ(3)条件に合うTの位置の特定が難しい。
使える情報が前問になかったか。相似が維持されることに気がつきたい。
△ATUが最大となるのは、1辺が最長となる相似図形。
理由の説明に迷ったら一か八か。こうじゃないかな?と予測して計算してしまうのも手。



コメント
いつも高校入試過去問の参考にさせていただいております!
ーーー
大問4のII(3)はこういう解き方もありますね
ーーー
I(2)より △PAQ∽△TAU
△PAQのある一辺の長さを①としたときの
△TAUのそれに対応する一辺の長さをVとすると
相似比は①:V、面積比は①:V²
つまり Vが長く(大きく)なるほど△TAUの面積も大きくなるから
ATが最長となる時を考えればよいと分かる。
それは ATが円Oの直径となる時である。
このとき AT=8√3/3 cmであるから
V=8√3/3÷4=2√3/3 cm
また 三平方の定理より AQ=√{(4+4)²+4²}=4√3 cm
よって AU=AQ×V=4√3×2√3/3=8
ゆえに 求める面積は
AT×AU÷2=8√3/3×8÷2=32√3/3 cm²
ーーー
こうするとII(4)がV²として一瞬で出せますね!
コメントありがとうございます。
こちらこそ、参考にさせて頂きますね。
サボ