2024年度　新潟県公立高校入試問題過去問【数学】解説

平均40.6点（前年比；＋0.9点）

問題はコチラ→ＰＤＦファイル

大問１（小問集合）－64.3％

（１）　93.7％
３－12＋７
＝－２

（２）　90.4％
３（２ａ－ｂ）－５（－ａ＋２ｂ）
＝６ａ－３ｂ＋５ａ－10ｂ
＝11ａ－13ｂ

（３）　91.2％
18ｘｙ²÷（－３ｙ）²
＝18ｘｙ²÷９ｙ²
＝２ｘ

（４）　50.2％
すべてを２乗する。
（３/10）²＝９/100
（√２/５）²＝２/25＝８/100
（１/√10）²＝１/10＝10/100
小さい順に示すと、√２/５＜３/10＜１/√10

（５）　56.8％
（ｘ＋５）²＝13
ｘ＋５＝±√13
ｘ＝－５±√13

（６）　51.3％
反比例→温まるまでの時間×レンジの出力＝一定
（500W×３分）÷600W＝２・１/２分＝２分30秒

（７）　33.3％

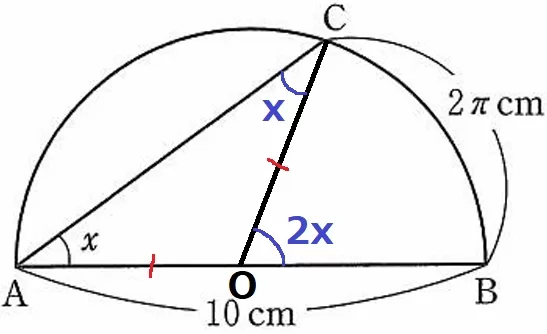
中心ＯとＣに補助線をひく。
半径より△ＡＯＣは二等辺→∠Ｃ＝ｘ
△ＡＯＣで外角定理→∠ＣＯＢ＝２ｘ

直径10ｃｍの円の円周は10πｃｍ。
扇形ＯＢＣの中心角である∠ＣＯＢ＝360×２π/10π＝72°
２ｘ＝72°
ｘ＝36°
*誤答例、30°

（８）　47.8％
抽出した100個のうち、赤：白＝10：90＝①：⑨
赤全部が300個なので、白全部は300×⑨＝2700個
*誤答例、3000個

大問２（小問集合２）－33.0％

（１）　64.7％
代表は７人中２人だから、Ａが選ばれる確率は２/７。
*Ａ以外が選ばれる確率も２/７。
＠＠
これで良いかなと思ったのですが、公式解答みたら説明問題でした(;´･ω･)
７人から２人選ぶ方法は、₇Ｃ₂＝21通り
Ａが含まれる代表２名の組み合わせは（ＡとＡ以外）の６通りで、確率は６/21＝２/７
計算不要な問題だと思うんですけどね。

（２）　28.7％！
説明問題。
ｙ＝ａｘ²において、ｘの値がｐ→ｑに増加するときに変化の割合はａ（ｐ＋ｑ）
ａ（１＋５）＝５ａ＝２ａ²
ａ≠０だから、両辺をａで割ることが許される。
２ａ＝５
ａ＝５/２

（３）　5.6％!!
どんな図形を描けばいいかはわかりやすいが、作図が難しい。

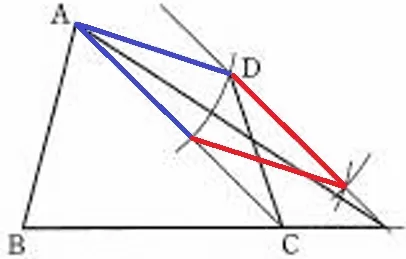
Ｄを通るＡＣに平行な線（もしくはＡを通るＢＤに平行な線）をひき、
ＢＣの延長線との交点を結べば、等積変形から四角形ＡＢＣＤと面積が等しい三角形が作れる。

公式解答はＡＤの長さで弧を描き（青線が等しい）、さらに同じ長さで２点から弧を描く（赤線が等しい）。
青線と赤線は等しいので、４辺が等しい菱形になる。
菱形の対辺は平行だからＡＣに平行な直線がひける。最後に半直線ＢＣとの交点とＡを結ぶ。

＠別解＠

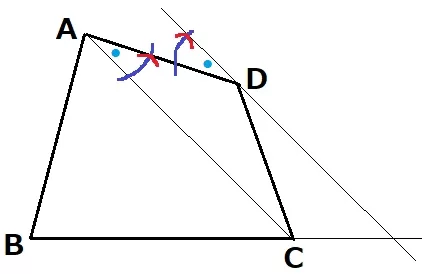
別のやり方として、教科書では習わないが角の移動で平行線をひく方法がある。
Ａ→Ｄの順で青い弧を描く。交点に針を合わせて赤い弧を描く。Ｄと交点を結ぶ。
錯角が等しくなり、ＡＣに平行な直線がひける。
角が等しい理由は、合同な二等辺三角形の対応する角だから。

大問３（平面図形）－38.8％

（１）　69.4％
正三角形で同じ形→△ＡＢＣ∽△ＤＥＦ
面積比は相似比の２乗だから、△ＡＢＣ：△ＤＥＦ＝６²：５²＝36：25
*誤答例、６：５

（２）①　59.3％
△ＡＧＬ∽△ＤＧＨの証明。

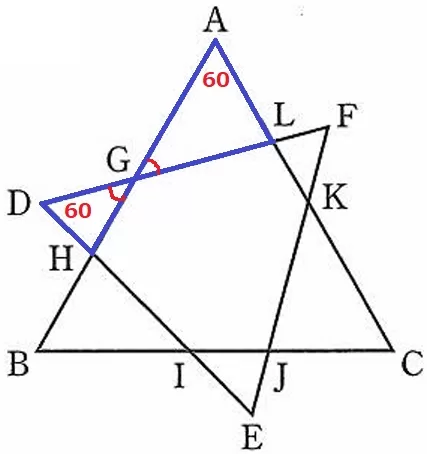
正三角形の内角60°と対頂角より、２角相等で∽

②　1.2％!!
説明問題。記述が大変。

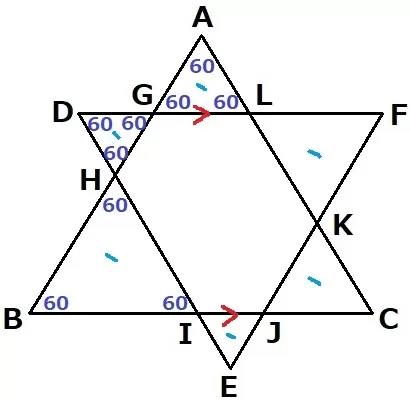
正三角形ＡＢＣやＤＥＦの内角、ＢＣ//ＤＦの錯角、対頂角から、
周囲の６つの三角形もすべて正三角形である。

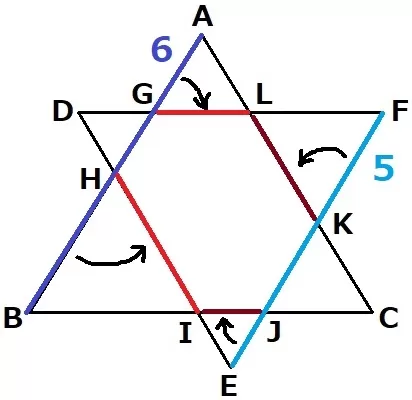
ＬＧ＝ＡＧ、ＨＩ＝ＨＢ
ＬＧ＋ＧＨ＋ＨＩ＝ＡＧ＋ＧＨ＋ＨＢ＝６ｃｍ（ＡＢの両端を折り曲げるイメージ）
同様に、ＩＪ＝ＥＪ、ＫＬ＝ＫＦから、
ＩＪ＋ＪＫ＋ＫＬ＝ＥＪ＋ＪＫ＋ＫＦ＝５ｃｍ
六角形ＧＨＩＪＫＬの周りの長さは、６＋５＝11ｃｍ

大問４（数量変化）－27.2％

（１）　71.2％
Ａは引き戸を動かす長さに応じて増えていく。
15秒後は、15×100＝1500ｃｍ²

（２）　49.3％

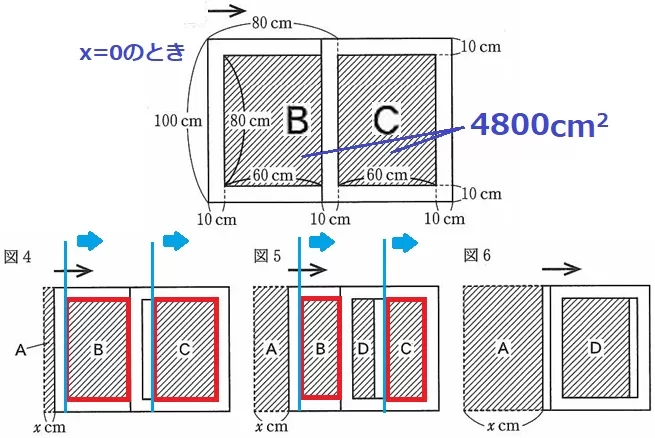
切片が4800ということは、ｘ＝０のときに4800ｃｍ²
ここからＢ・Ｃと判断できる。
その後の変化をみていくと、水色のラインが動くことでＢとＣは同じ割合で減少していく。
つまり、ＢとＣは常に同じ面積である。
ア…Ｂ・Ｃ

（３）　22.2％！

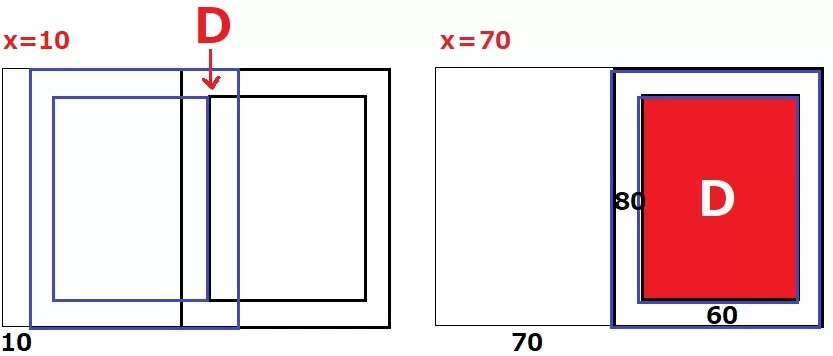
Ｄが始まるのは10秒後。
スタートはｘ＝10のとき、ｙ＝０
Ｄの変化が終わるのは引き戸を完全に動かした70秒後。
ｘ＝70のとき、ｙ＝60×80＝4800

（10、０）→（70、4800）
右に60、上に4800なので、傾きは4800/60＝80
切片は（10、０）から左に10、下に10×80＝800移動して－800。
ｙ＝80ｘ－800
Ｄの面積ｙは80ｘ－800ｃｍ²

（４）　11.5％！
グラフの転換点を調べる。

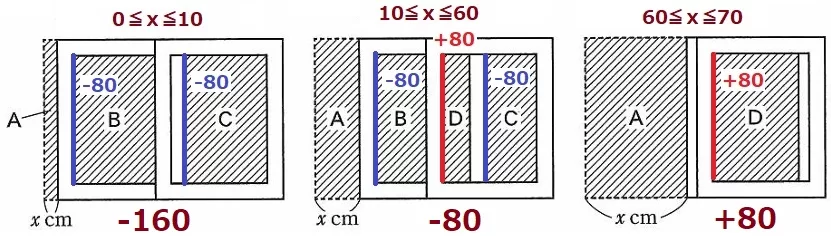
Ｄが現れる前の０≦ｘ≦10ではＢとＣが減少する。
ｘが１増加するたびに、ＢとＣの面積はそれぞれ縦80ｃｍ²減っていく。
変化の割合：－80－80＝－160

ＢとＣが消えるまでの10≦ｘ≦60ではＢとＣが－80ずつ減少、Ｄが＋80増加する。
変化の割合：－80×２＋80＝－80

最後の10秒間の60≦ｘ≦70ではＢとＣは０ｃｍ²、Ｄが＋80増加する。
変化の割合：＋80

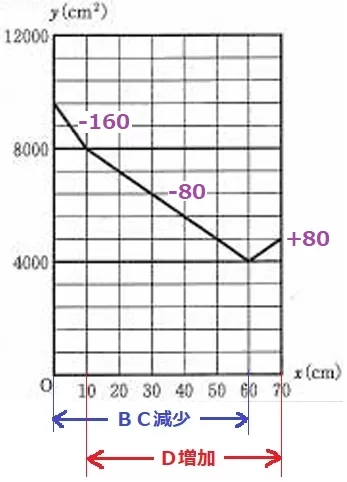
縦軸は１目盛り800。
ｘ＝０、ｙ＝Ｂ＋Ｃ＝60×80×２＝9600
ｘ＝10、ｙ＝9600－160×10＝8000
ｘ＝60、ｙ＝8000－80×50＝4000
ｘ＝70、ｙ＝4000＋80×10＝4800

（５）　3.8％!!
説明問題。

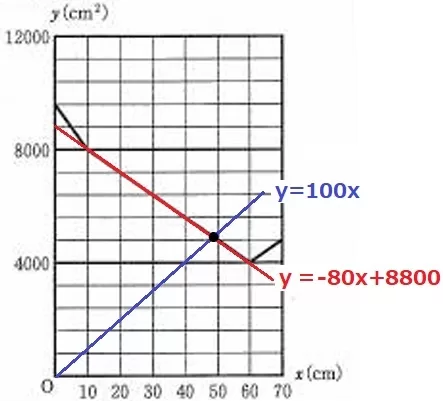
引き戸が１ｃｍ移動するたびに、Ａは100ｃｍ²ずつ増加する。
Ａ；ｙ＝100ｘ
先ほどのグラフにＡを描くと、10≦ｘ≦60のときに交わる。
このときの直線の式は傾きが－80、切片は線分を延長して＋8800
→ｙ＝－80ｘ＋8800
100ｘ＝－80ｘ＋8800
ｘ＝440/９
これは10≦ｘ≦60に適する。

大問５（空間図形）－19.7％

（１）　73.9％

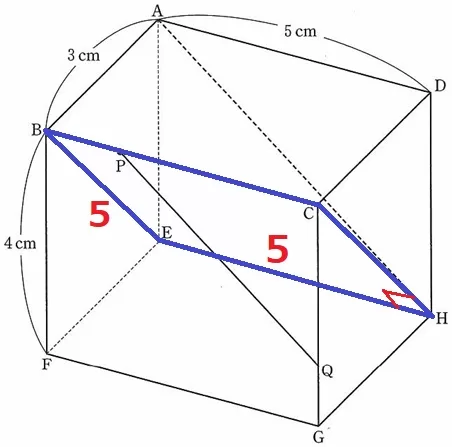
△ＡＢＥで三平方→辺の比は３：４：５だから、ＢＥ＝５ｃｍ

（２）　60.4％
ＢＣとＥＨは面ＡＢＦＥ、面ＤＣＧＨに対して垂直。
四角形ＢＣＨＥの内角がすべて90°→長方形
面積は５×５＝25ｃｍ²

（３）①　0.8％!!!
説明問題。

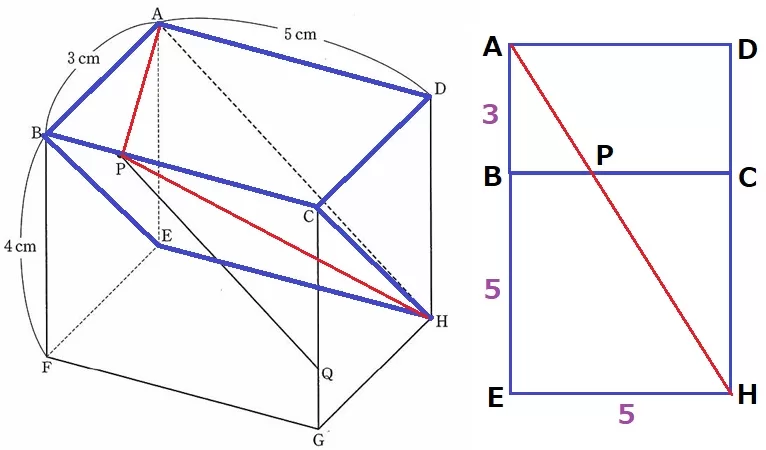
最短距離なので展開図を作成だが、面の傾きが普通じゃない(;´･ω･)
ＡＰとＰＨを含む、面ＡＢＣＤと面ＢＥＨＣを折り曲げて平面にする。
四角形ＢＥＨＣは前問より１辺５ｃｍの正方形。
△ＡＢＰ∽△ＡＥＨから、ＢＰ＝５×３/８＝15/８ｃｍ

②　0.2％!!!
説明問題。

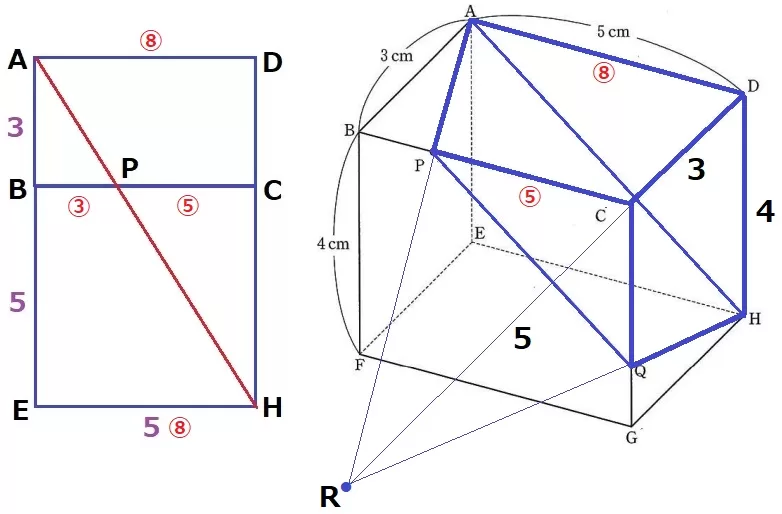
前図でＢＰ＝③とすると、ＥＨ＝ＡＤ＝⑧、ＰＣ＝⑤

ＡＰ・ＤＣ・ＨＱを延長した交点をＲとする。
三角錐Ｒ―ＰＱＣ：三角錐Ｒ―ＡＨＤ＝⑤：⑧
体積比は相似比の３乗で【125】：【512】→求積すべき角錐台は差の【387】
ＲＣ：ＣＤ＝５：３で、ＣＤ＝３ｃｍだからＲＤ＝８ｃｍ
角錐台の体積は、５×４÷２×８÷３×【387】/【512】＝645/32ｃｍ³