問題PDF
図1に示した葉Aと葉Bの形を比べることにしました。
はじめに、図2に示した測定方法にしたがって、縦方向を長さ、横方向を幅として測り、平面部の形を調べました。ここでは、平面部の縦方向の長さの最大値を全長とよび、横方向の幅の最大値を最大幅とよびます。

次に、葉A、葉Bそれぞれの全長と最大幅から、全長に対する最大幅の割合「最大幅÷全長×100(%)」を計算しました(表1)。ただし、表1の①、②が葉A、葉Bの順番になっているとは限りません。

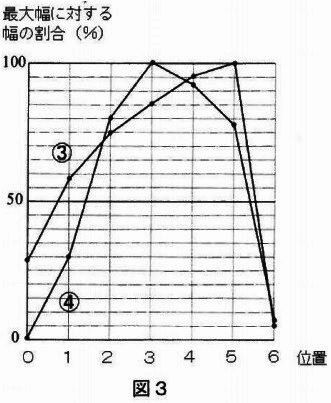
さらに、葉の先たん部を位置0として、全長を6等分した位置0~6の各位置(図1)の幅を調べました。図3のグラフは葉Aと葉Bそれぞれについて、横軸に位置をとり、縦軸に「最大幅に対するその位置での幅の割合(%)」をとって点で表し、それを直線で結んで作りました。
問1
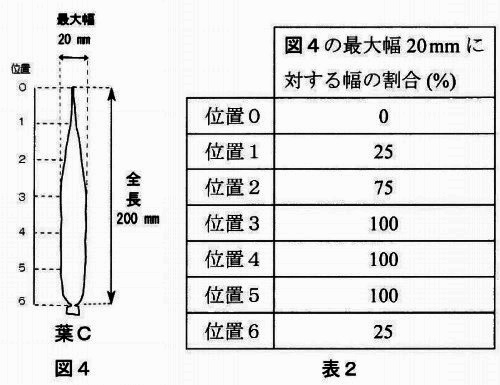
表1の①・②と図3の③・④からそれぞれ葉Aのものを選んだ組み合わせを選びなさい。
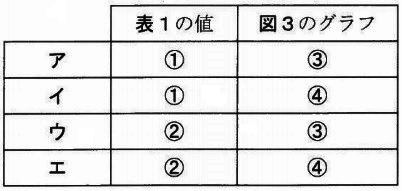
次に、図4で示した葉Cの形を調べることにしました。葉の全長を6等分した位置0~6の各部分について、「最大幅に対する幅の割合(%)」が表2に示されています。
問2
葉Cの位置0~6での幅の値を表2から計算し、下の例1にならい、
値を解答らんに点で書き入れ、各点を直線で結びなさい。
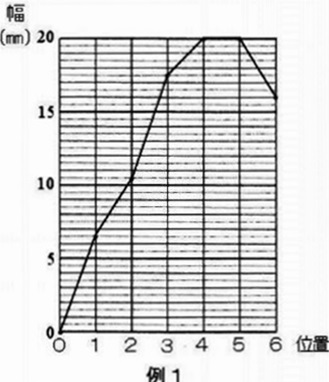
次に、図5のように葉Cが成長して全長20mmの幼葉から全長200mmの成葉になるときの形の変化を調べました。ここでいう幼葉とは成長中の葉で、成葉とは大きくなって成長をやめた葉です。
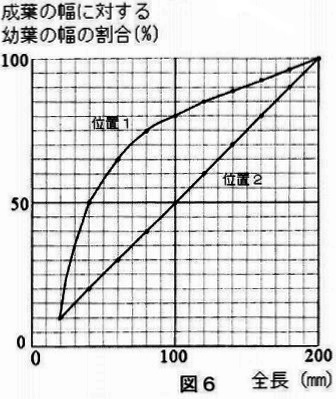
成長によって、葉の全長が変化するそれぞれの段階で、葉の全長を6等分して位置0~6とします(図5)。葉の縦方向の成長は、位置0~6のそれぞれの間かくが同じ割合で広がるようにおこるものとします。ここで位置1について、「成葉の幅に対する幼葉の幅の割合(%)」を各成長段階で調べます。図6は横軸を全長とし、縦軸を「成葉の幅に対する幼葉の幅の割合(%)」として、成長とともに位置1の幅がどのように変化していくかを示したものです。位置2も同様にして調べ、その結果も図6に重ねて示しています。

問3
葉の全長が20mm、40mm、100mmのとき、位置1、位置2での幅の値を表2、
図6をもとに計算し、下の例2にならい、値を問2の解答らんに点で書き入れなさい。
それぞれの点の右側に20mmはカ、40mmはキ、100mmはクと記入すること。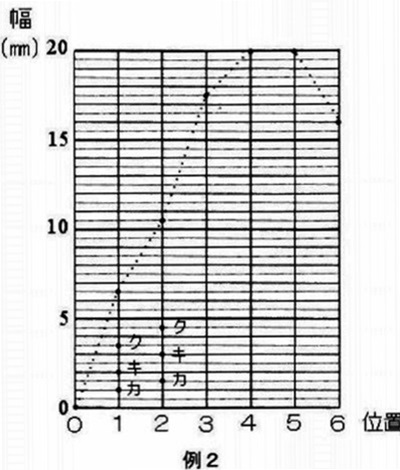
問4
幅の増加量が位置2より位置1で多い期間を、次のなかから選びなさい。
ア:葉の全長が20mmから40mmまで成長する期間
イ:葉の全長が40mmから100mmまで成長する期間
ウ:葉の全長が100mmから200mmまで成長する期間
問5
葉の①全長が20mmから40mmまでの成長する期間と、②全長が100mmから200mmまで成長する期間では、ともに葉の全長は2倍になります。問3の位置1の結果をもとに考えると、下線部①、②のそれぞれの期間について、葉のCの先たん(位置0~1)の長さと幅の比率はどうなりますか。もっとも近いものを、次のなかからそれぞれ1つずつ選びなさい。ただし、下図は長さと幅の比率を表したものであり、成長前後の長さの変化量を正確に表したものではありません。

ア:長さに比べて幅の比率が小さくなる。
イ:長さに比べて幅の比率が大きくなる。
ウ:長さと幅の比率は変わらない。
@解説@
問1:エ

葉Aは縦長、葉Bは横長。

最大幅(横)÷全長(縦)をするので、値が大きいと横長。
①B、②A

③位置5まで広がる葉B
④位置3まで広がる葉A
組み合わせはエ
問2:下記グラフ参照
表2をもとに計算する。
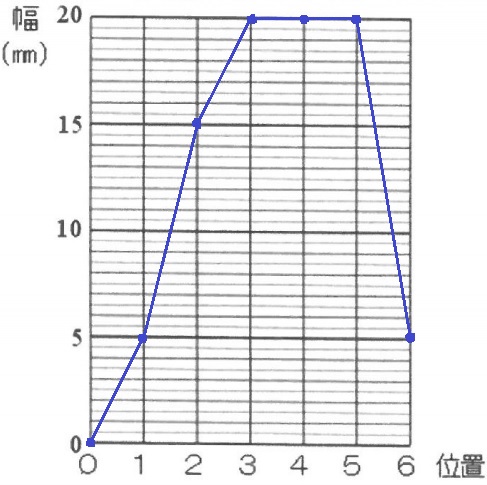
位置0:20mm×0%=0mm
位置1:20mm×25%=5mm
位置2:20mm×75%=15mm
位置3:20mm×100%=20mm
位置4:20mm×100%=20mm
位置5:20mm×100%=20mm
位置6:20mm×25%=5mm
問3:下図参照

図6はどのくらい横幅が広がるかを表している。
縦軸が100%になると大人の葉(全長200mの成葉)で成長が止まる(横幅の最大値)
葉の全長が20mmのときからはじめ、位置1では横幅がグングン広がり、
成葉に近づくにつれて、広がる割合が小さくなる。
対して、位置2は比例的に広がっている。
■位置1
全長20mmのとき、図6より幼葉の横の割合は10%
(2)より全長200mmの成葉における位置1の幅は5mm
よって、5mm×10%=0.5mm(カ)
同様に全長40mmでは、5mm×50%=2.5mm(キ)
全長100mmでは、5mm×80%=4.0mm(ク)
■位置2
(2)より成葉の幅は15mm
15mm×10%=1.5mm(カ)
15mm×20%=3.0mm(キ)
15mm×50%=7.5mm(ク)

↑プロットするとこうなる。
素早い読解力と処理能力が問われた。
問4:ア
図6から最初の方では?と予測できてしまうが、
割合ではなく増加量なので、先ほどの数値を利用する。
全長;20mm→40mm→100mm→200mm
位置1;0.5mm→2.5mm→4.0mm→5.0mm
位置2;1.5mm→3.0mm→7.5mm→15.0mm
20~40mmの差;【位置1】2.5-0.5=2.0mm【位置2】3.0-1.5=1.5mm
40~100mmの差;【位置1】4.0-2.5=1.5mm【位置2】7.5-3.0=4.5mm
100~200mmの差;【位置1】5.0-4.0=1.0mm【位置2】15.0-7.5=7.5mm
位置1で幅の増加量が大きい期間は、葉の全長が20~40mmまで成長する期間。
問5:①イ、②ア
・葉の縦方向(位置0~6)は、葉の全長が伸びるとともに同じ割合で広がっていく。
・位置0は葉の先端なので横幅は0mm。
①全長が20~40mmまで成長する期間
縦は2倍に伸びる。
位置1の横は0.5mm→2.5mmなので5倍伸びる。
ということは横長に広がっていく。
②全長が100~200mmまで成長する期間
縦は2倍に伸びる。
位置1の横は4.0mm→5.0mmなので5/4倍伸びる。
ということは縦長に広がっていく。
@余談@
ところで、どうして葉Cの先端部が横長から縦長へと変化するのか。
その仕組みと理由が設問では問われなかった。
推測になりますが、葉を伸ばす方向は細胞分裂がよく行われる場所を変えたり、
分裂した細胞をどちらに伸ばすかで調整しているのではないでしょうか。
先端部が最初は横長に広がっていく理由ですが、動くことのできない植物は、
太陽光をいかに自分の葉に当てられるかが勝負になるので、
その植物にとって光合成の効率を良くするために最も都合がいい形に変えるのだと思います。
若い葉っぱは植物の上部にできるので、横に伸ばした方が素早く葉の面積を広げられる。
成長につれて新しい葉が自分の上にどんどんできるため、葉に光が当たらなくなっていくと、
葉Cを含む植物の他の葉と同じ形(先端がシュッと細くなる形)にシフトするのだと思います。
■追記
後日、調べてみたら葉の先端が細くなる理由がわかりました。
葉っぱの先はなぜ尖っているのか(日本植物生理学会)
柴岡さんの回答によると、はじめは少数の細胞で細胞分裂を繰り返して葉が大きくなるのですが、
途中で細胞分裂を繰り返す場所を葉の根元に限定するようになるそうです。
先端部は最初の少数の細胞で作られたのであまり大きくならず細くなり、
先端より下は細胞数が増えたあとに細胞分裂でぐんぐん幅を広げたからということでした。
植物の葉の形にも奥深い科学の世界があったとは( ˘ω˘ )


コメント