2021年度　佐賀県公立高校入試問題過去問【数学】解説

問題はコチラ→ＰＤＦファイル
出題範囲の除外はなし。

大問１（小問集合）

（１）ア
５－（－７）
＝５＋７
＝12

イ
－８÷４/３
＝－６

ウ
ｘ＋３ｙ－２（ｘ－ｙ）
＝ｘ＋３ｙ－２ｘ＋２ｙ
＝－ｘ＋５ｙ

エ
（√２－１）²
＝２－２√２＋１
＝３－２√２

（２）
ｘ²＋２ｘ－35
＝（ｘ－５）（ｘ＋７）

（３）
ｘ²＋５ｘ＋１＝０
解の公式を適用して、
ｘ＝（－５±√21）/２

（４）
体積比は相似比の３乗。
F：G＝３³：５³＝27：125
Ｇの体積は、81π×125/27＝375πｃｍ³

（５）

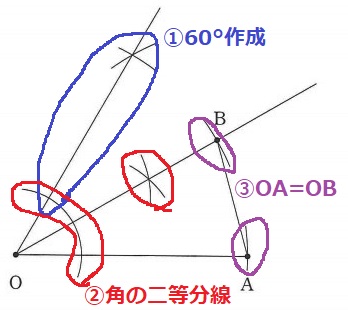
①ＯＡの長さをとり、ＯとＡから弧を描く。
交点はＯＡを１辺とする正三角形の頂点で60°が作れる。
②角の二等分線で30°を作成。
③ＯＡの長さを二等分線に移す。交点がＢ。

（６）

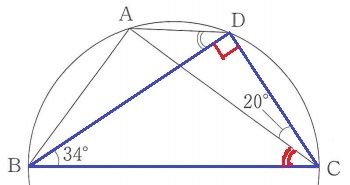
円周角定理より、∠ＡＤＢ＝∠ＡＣＢ
直径に対する円周角で∠ＢＤＣ＝90°
△ＢＣＤの内角より、180－（90＋34＋20）＝36°

（７）

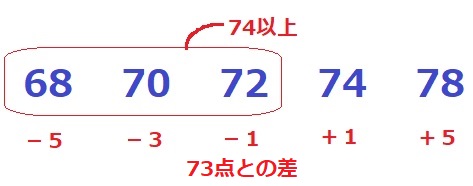
値を昇順に並べかえる。
５個の中央値（メジアン）は３番目の値だから72。
中央値を74にするには、68・70・72のいずれかを74以上にする。

平均値となる73点との差を考える。
－５－３－１＋１＋５＝－３
68・70・72のいずれかを＋３すれば73点で均せる。
このうち、74点以上になるのは72＋３＝75のみ。
①Ｅ、②75分

大問２（方程式）

（１）ア
Ａ中学の人数をｘ、Ｂ中学の人数をｙとする。
１つ目は人数の合計で等式。
ｘ＋ｙ＝45
２つ目は山の希望者の合計で等式
20/100ｘ＋40/100ｙ＝14
もしくは、海の希望者でも良い。
80/100ｘ＋60/100ｙ＝31
①ｘ＋ｙ、②20/100ｘ＋40/100ｙ＝14（80/100ｘ＋60/100ｙ＝31）

イ
先ほどの連立を解く。
ｘ＋ｙ＝45　…①
20/100ｘ＋40/100ｙ＝14
10倍して、２ｘ＋４ｙ＝140　…②

サボは②－①×２をしました。
すると、２ｙ＝50
ｙ＝25
①に代入して、ｘ＝20
Ａ中学校…20人　Ｂ中学校…25人

（２）ア
縦；３ｃｍ
横；３＋２＝５ｃｍ
面積は３×５＝15ｃｍ²

イ
底辺をｘとすると高さは３ｘ。
ｘ×３ｘ÷２＝６
ｘ²＝４
ｘ＞０だから、ｘ＝２
２ｃｍ

ウ
答案では求める過程も記述する。

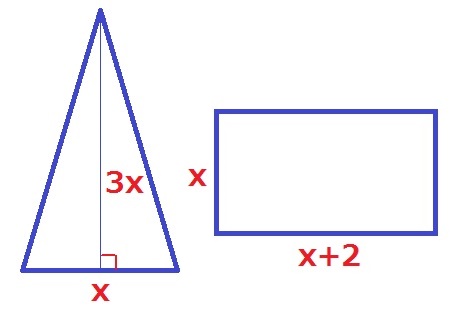
ｘ×３ｘ×１/２＝ｘ（ｘ＋２）＋６
ｘ²－４ｘ－12
＝（ｘ－６）（ｘ＋２）＝０
ｘ＞０だから、ｘ＝６
６ｃｍ

大問３（確率＆整数）

（１）ア
６×６＝36通り
*重複はない。

イ
偶数⇒一の位が２・４・６になればいい。
一の位だけを考え、６個のうち３通り。
３/６＝１/２

ウ
３の倍数⇒位の和が３の倍数
12・21
15・51、24・42、33
36・63、45・54
66
以上、12通り。
12/36＝１/３

エ

頭の中で表をイメージ(´ω`).。0
斜め線がゾロ目で、位の数をひっくり返しても同数になる。
はじめの数が大きいのは、５＋４＋３＋２＋１＝15通り
（もしくは、対称性から（全体－同数）÷２＝（36－６）÷２＝15通り）
15/36＝５/12

（２）ア
いわゆるガウス記号の問題。
ある値について、それを超えない最大の整数を求める。
*本物のガウス記号は[　]←これです。

７≦7.3＜７
〈7.3〉＝７

イ
〈ｎ/４〉＝５
５≦ｎ/４＜６　←４倍
20≦ｎ＜24
21～23のどれか１つを挙げる。

ウ
６≦ｎ/４＜11
24≦ｎ＜44

最小値24、最大値43。
43－24＋１＝20個

大問４（関数）

（１）
ｙ＝ａｘ²にＡ座標を代入。
２＝２²ａ
ａ＝１/２

（２）
ｙ＝１/２ｘ²にｘ＝４を放り込む。
ｙ＝１/２×４²＝８

（３）
Ｂ（－６、18）⇒Ｃ（４、８）
右に10、下に10だから、傾きは－10/10＝－１

Ｃ座標から左に４、上に４移動して、
切片は８＋４＝12

（４）

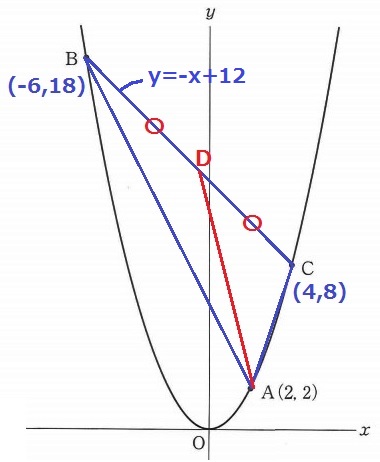
交点をＤとする。ＤはＢＣの中点。
Ｄのｘ座標は、（－６＋４）÷２＝－１
これを前問で求めたｙ＝－ｘ＋12に代入。
ｙ＝－（－１）＋12＝13
（－１、13）

（５）ア

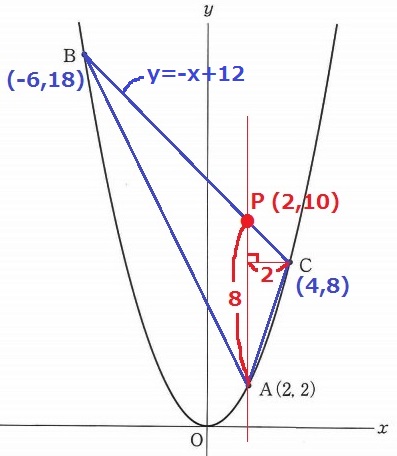
Ｐのｘ座標は２。
これをｙ＝－ｘ＋12に代入してＰ（２、10）。

△ＰＡＣの底辺ＰＡは８、高さは２だから、
８×２÷２＝８

イ
２個前の問題で△ＡＢＣの面積を２等分する直線を求めたので、
これを活用できないかを考える。

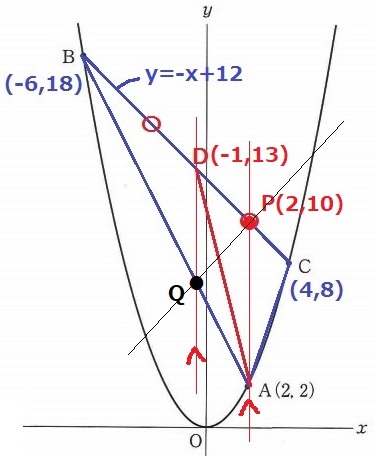
Ｄを通るＡＰに平行な線分をひくと、
これとＡＢとの交点がＱとなる。
なぜなら、等積変形で△ＡＰＤと△ＡＰＱの面積が等しく、
△ＡＣＤ＝△ＡＰＤ＋△ＡＰＣ
四角形ＡＣＰＱ＝△ＡＰＱ＋△ＡＰＣ
…で△ＡＢＣの半分である△ＡＣＤと四角形ＡＣＰＱの面積は等しいから。

Ｑのｘ座標は－１。
ｘ座標の差より、ＡＱ：ＱＢ＝３：５
Ｑのｙ座標は、２＋（18－２）×３/８＝８
Ｑ（－１、８）

大問５（平面図形）

（１）
△ＡＣＥで三平方。
ＡＥ＝√５ｃｍ

（２）
△ＡＥＣ∽△ＢＥＤの証明。

図で示すほどのものでもなかったが。。
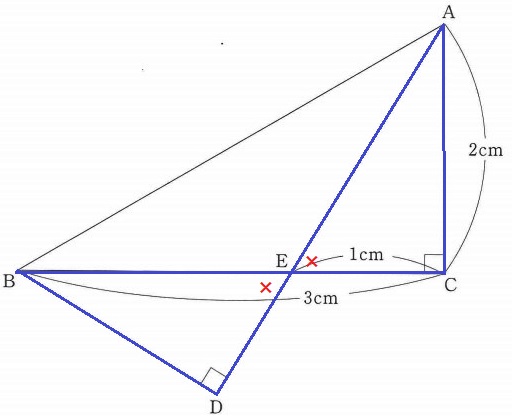
仮定の直角と対頂角が２角相等→∽

（３）
小学生でも解ける。

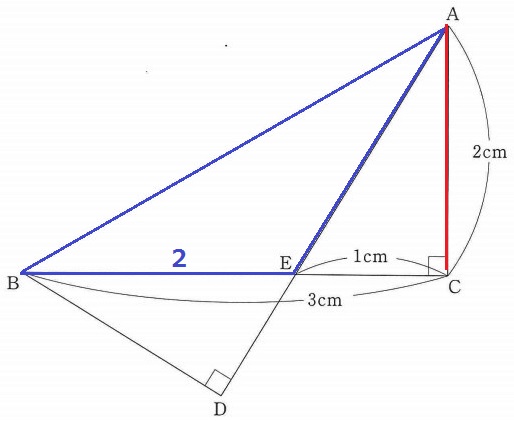
底辺をＢＥとしたとき、高さはＡＣ。
２×２÷２＝２ｃｍ²

（４）ア

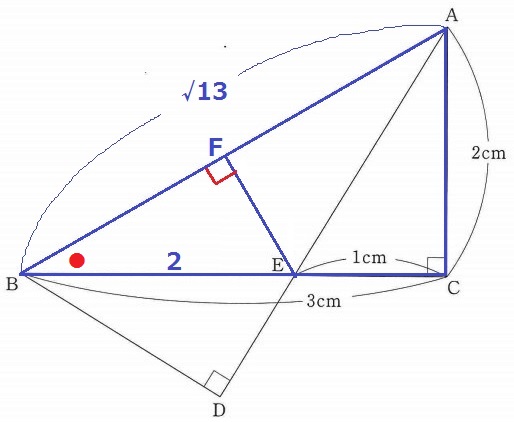
ポイントは、２角相等で△ＡＢＣ∽△ＥＢＦ。
△ＡＢＣで三平方→ＡＢ＝√13ｃｍ

ＥＢ：ＥＦ＝ＡＢ：ＡＣ＝√13：２
ＥＦ＝２×２/√13＝４√13/13ｃｍ

イ

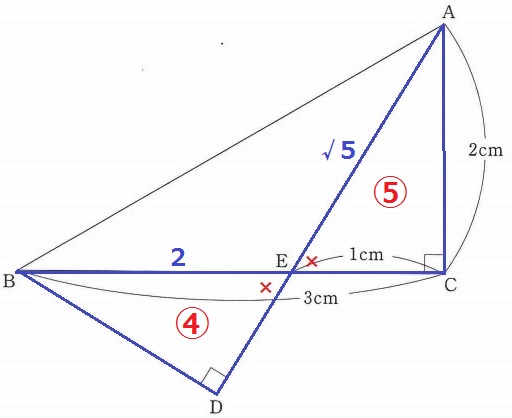
△ＢＥＤが△ＡＢＣ外にあって求めにくい。
そこで（２）△ＡＥＣ∽△ＢＥＤの面積比から考えてみる。
ＢＥ：ＡＥ＝２：√５
面積比は相似比の２乗だから、△ＢＥＤ：△ＡＥＣ＝④：⑤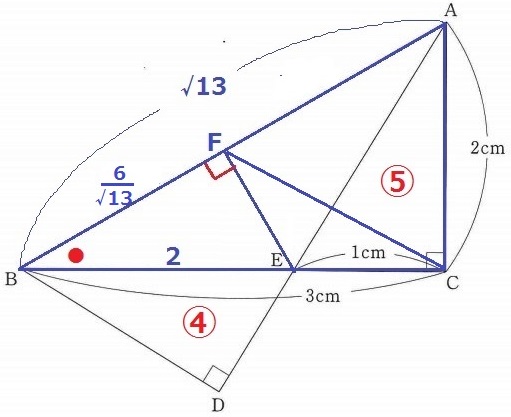
△ＡＥＣと△ＥＣＦは底辺がＥＣで共通する。
ということは、高さの比が面積比に値する。
△ＡＥＣと△ＥＣＦの高さの比はＡＢ：ＦＢ。

前問の△ＡＢＣ∽△ＥＢＦで、ＥＢ：ＢＦ＝ＡＢ：ＢＣ＝√13：３
ＦＢ＝２×３/√13＝６/√13ｃｍ

ＡＢ：ＦＢ＝√13：６/√13＝13：６
△ＥＣＦの面積比は、⑤×６/13＝〇30/13

したがって、△ＥＣＦ（Ｓ₁）：△ＢＥＤ（Ｓ₂）
＝〇30/13：④
＝30：52
＝15：26