2023年度　石川県公立高校入試問題過去問【数学】解説

平均44.4点（前年比；－2.8点）
問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）ア
５－（－４）
＝５＋４
＝９

イ
（－３）²×２－８
＝９×２－８
＝10

ウ
15/２ｘ³ｙ²÷５/８ｘｙ²
＝12ｘ²

エ
（４ａ－２ｂ）/３－（３ａ＋ｂ）/４
＝｛４（４ａ－２ｂ）－３（３ａ＋ｂ）｝/12
＝（16ａ－８ｂ－９ａ－３ｂ）/12
＝（７ａ－11ｂ）/12

オ
√54－２√３÷√２
＝３√６－√６
＝２√６

（２）
反比例の比例定数ａはｘとｙの積で一定（ａ＝ｘｙ）。
ａ＝２×（－６）＝－12
ｙ＝－12/ｘ

（３）
√60＝２√15
√15の根号を外すには、根号の中で15をかければいい（√15×√15＝15）。
ｎ＝15

（４）
全体はａｍＬ、配ったのは７ｂｍＬ。
残りは200ｍＬより少ない≒配った量より200ｍＬの方が多い。
ａ－７ｂ＜200

（５）

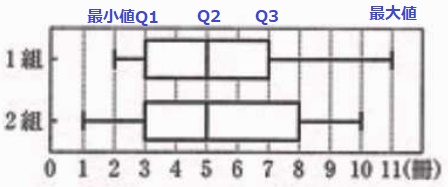
ア：平均値を×印などで記す箱ひげ図もあるが、本問はわからない。×
イ：第３四分位数（Q3）は１組…７冊、２組…８組。〇
ウ：四分位範囲＝Q3－Q1、１組…４冊、２組…５冊。×
エ：31人のQ3は上位15人の真ん中、上から８番目。
　いずれもQ3が７冊以上→少なくとも８人は７冊以上読んだ。〇
オ：10冊の生徒について、最大値から２組はいるが１組は不明。×
イ・エ

大問２（確率）

（１）
和が４の組合わせは（赤１、赤３）（白１、赤３）（赤２、白２）の３通り。

（２）
答案では図や表、式などを用いて考え方を説明する。

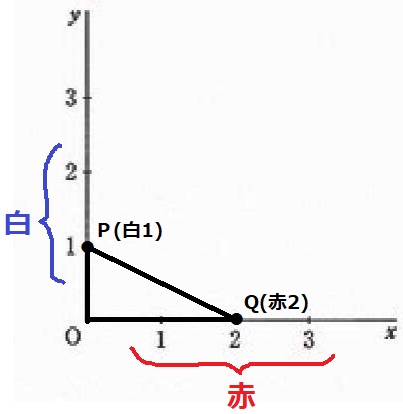
たとえば、１回目で白１を取るとＰ（０、１）
２回目で赤２を取るとＱ（２、０）となり、△ＯＰＱは三角形になる。
つまり、三角形ができるにはＰとＱが異なる軸上にいる必要がある。
言い換えれば、異色を出す。

『もとに戻さずに続けて２回取り出す』⇒一度に２個とるのと同じ。
５個から２個取り出す組み合わせは、₅Ｃ₂＝10通り

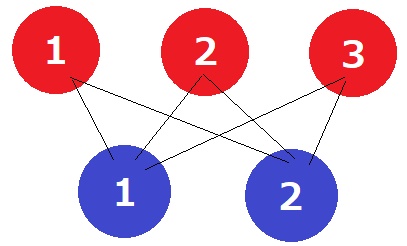
異色の組み合わせは上図のように考え、２×３＝６通り
異色を取り出す確率は、６/10＝３/５

大問３（関数）

（１）
周の長さが22ｃｍ。縦と横の和（半周）は22÷２＝11ｃｍ
縦の長さをａとすると、横はａ＋３。
ａ＋（ａ＋３）＝11
ａ＝４
４ｃｍ

（２）
正方形の枠をつくる。
ｘ＝８のとき、１辺は２ｃｍ→ｙ＝２²＝４
ｘ＝20のとき、１辺は５ｃｍ→ｙ＝５²＝25
変化の割合＝（ｙの増加量）/（ｘの増加量）＝（25－４）/（20－８）＝７/４

（３）
答案では途中の計算も書く。

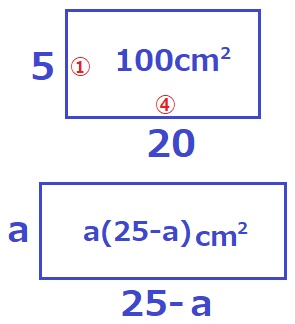
ｘ＝50のときのｙの値をそれぞれ求める。
一方は、縦：横＝①：④の比率をキープする。
⑤＝50÷２＝25ｃｍ→縦①＝５ｃｍ、横④＝20ｃｍ
ｙ＝５×20＝100

他方は、縦の長さをａで固定する。
横の長さは25－ａ。長方形の面積は、ｙ＝ａ（25－ａ）

どちらの点がどちらの長方形か。
縦：横＝①：④の長方形は周の長さｘが伸びるにつれて、縦と横の双方が伸びる→ｙ＝ａｘ²
もう１つの長方形は縦をａで固定するので、横しか伸びない→ｙ＝ａｘ＋ｂ（一次関数）
つまり、下の点がｙ＝100。上の点はｙ＝100＋14＝114

ａ（25－ａ）＝114
ａ²－25ａ＋114
＝（ａ－６）（ａ－19）＝０
ａ＜25/２なので、ａ＝６

大問４（方程式）

とり肉１パックをｘｇ、ぶた肉１パックをｙｇとする。
重さ（ｇ）で等式。
ｘ＋２ｙ＝720　…①

もう１つは金額で等式を立てる。
表は100ｇあたりなので、これをｘｇ、ｙｇに変換する。
120円×（ｘ/100）ｇ＋150円×（２ｙ/100）ｇ＝1020円
６/５ｘ＋３ｙ＝1020　←５倍
６ｘ＋15ｙ＝5100　←÷３
２ｘ＋５ｙ＝1700　…②

②－①×２をすると、ｙ＝260
①に代入、ｘ＝720－２×260＝200
とり肉…200ｇ　ぶた肉…260ｇ

大問５（作図）

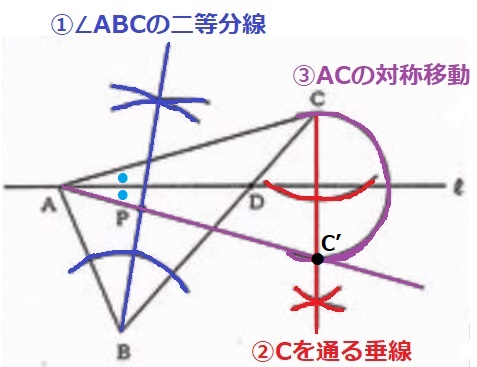
●∠ＡＢＰ＝∠ＣＢＰ→ＢＰ共通だがＰ不明。ＡＢとＣＢがなす角に着目→∠ＡＢＣの二等分線
●∠ＤＡＰ＝∠ＤＡＣ→ＤＡ共通。ＰはＢと同じく直線ℓより下にある→ℓに対してＣを下に対称移動
→ＡＣを下に対称移動した直線上にＰがある（対称の軸であるℓが∠ＣＡＰを二等分する）。
①∠ＡＢＣの二等分線
②Ｃを通るℓに対して垂直な垂線。
③ℓ上の交点に針を合わせ、Ｃを下に対称移動。Ａと結び、①との交点がＰとなる。

＠別解＠

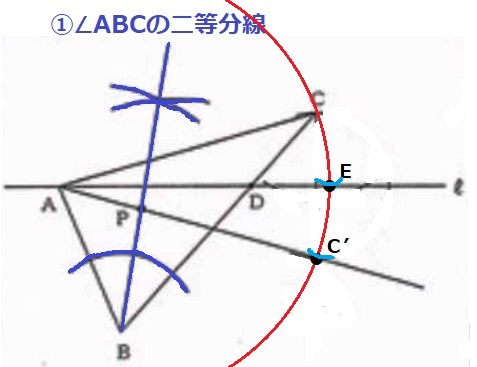
後半は角の移動でも描ける。
ＡＣの弧を描く→ℓ上の点をＥとすると、ＣＥの長さをとりＥから下に移す。
→弧との交点がＣ’となり、ＡＣ’を結ぶ。

大問６（空間図形）

（１）

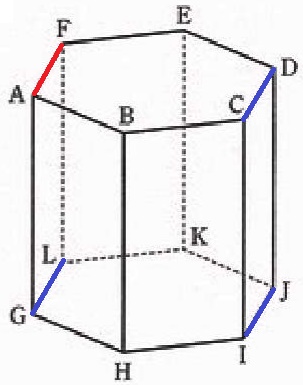
正六角形の対辺は平行。
辺ＡＦに平行なのは、辺ＣＤ・辺ＩＪ・辺ＧＬ。

（２）
答案では途中の計算も書く。

底面の正六角形と六角柱の高さは垂直→ＡＧ⊥ＧＩ
ＡＩを斜辺とする直角三角形ＡＧＩに着目する。
ＡＧ＝８ｃｍ、ＧＩの長さが知りたい。

正六角形の内角の１つは120°→△ＧＨＩの内角は30°－30°－120°の二等辺三角形。
これを二等分すると辺の比が１：２：√３の直角三角形になる。
ＧＩ＝４×√３/２×２＝４√３ｃｍ
△ＡＧＩで三平方→ＡＩ＝４√７ｃｍ

（３）
答案では途中の計算も書く。

六角柱の体積を求める。
底面の正六角形を６分割すると、１辺４ｃｍの正三角形ができる。
１：２：√３から高さは２√３ｃｍ。底面積は正三角形の面積を６倍すればいい。
六角柱の体積は、４×２√３÷２×６×８＝192√３ｃｍ³
立体ＭＮ―ＩＪＫＬの体積が、192√３÷12＝16√３ｃｍ³になればいい。

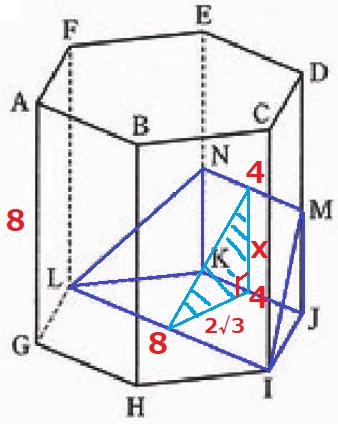
立体ＭＮ―ＩＪＫＬを上図のように２等分する。
立体は対称面について左右対称である。
ＭＪの高さをｘとすると、対称面の面積は２√３×ｘ÷２＝√３ｘｃｍ²

これを底面と捉え、断頭三角柱の考えを用いて体積を求める。
高さの平均はＭＮ・ＪＫ・ＩＬの平均→（４＋４＋８）÷３＝16/３ｃｍ
体積で方程式を立てると、√３ｘ×16/３＝16√３/３ｘ＝16√３
ｘ＝16√３÷16√３/３＝３ｃｍ
ＤＭ＝８－３＝５ｃｍ
ＤＭ：ＭＪ＝５：３

＠別解＠

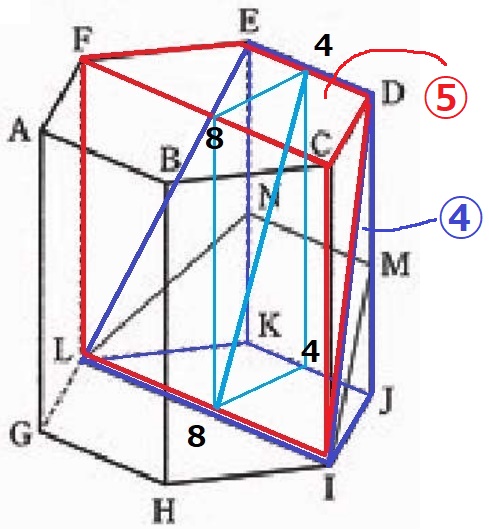
六角柱の半分を面ＤＥＬＩで分割する。
ＤＥ―ＩＪＫＬ（青）とＩＬ―ＣＤＥＦ（赤）の体積比を断頭三角柱を使って求める。
底面とみなす対称面は等しいので、高さの平均が体積比になる。
ＤＥ―ＩＪＫＬ…ＤＥ・ＪＫ・ＩＬの平均＝（４＋４＋８）÷３＝16/３
ＩＬ―ＣＤＥＦ…ＤＥ・ＣＦ・ＩＬの平均＝（４＋８＋８）÷３＝20/３
体積比は、ＤＥ―ＩＪＫＬ：ＩＬ―ＣＤＥＦ＝16/３：20/３＝④：⑤
六角柱の体積比は、（④＋⑤）×２＝⑱

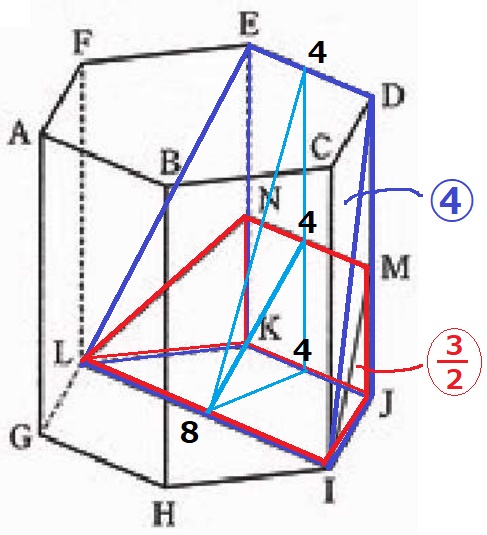
ＭＮ―ＩＪＫＬの体積比は、⑱÷12＝〇３/２
ＤＥ―ＩＪＫＬとＭＮ―ＩＪＫＬの高さ平均は（４＋４＋８）÷３で等しい。
→２つの立体の体積比は対称面である底面積の比に等しい。
そして、対称面は底辺共通なので、体積比は高さの比のＤＪ：ＭＪに相当する。
ＤＪ：ＭＪ＝ＤＥ―ＩＪＫＬ：ＭＮ―ＩＪＫＬ＝④：〇３/２＝８：３
ＤＭ：ＭＪ＝５：３

大問７（平面図形）

（１）

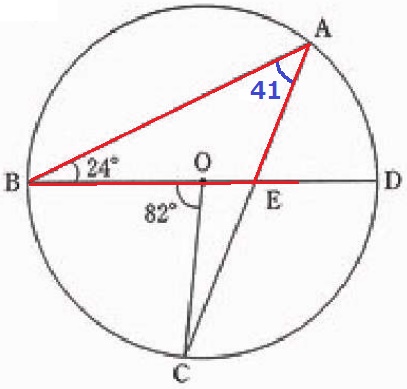
弧ＢＣの円周角で、∠ＢＡＣ＝82÷２＝41°
△ＡＢＥで外角定理→∠ＡＥＤ＝24＋41＝65°

（２）
△ＡＢＤ≡△ＣＡＦの証明。

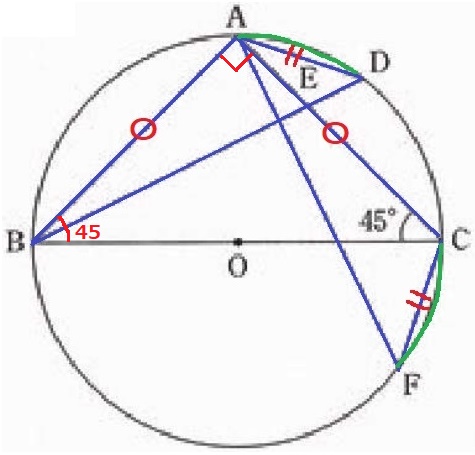
弧ＡＤ＝弧ＣＦから、弦ＡＤ＝弦ＣＦ
直径ＢＣに対する円周角→∠ＢＡＣ＝90°
△ＡＢＣの内角は45°―45°―90°だから直角二等辺三角形。
ＢＡ＝ＡＣ

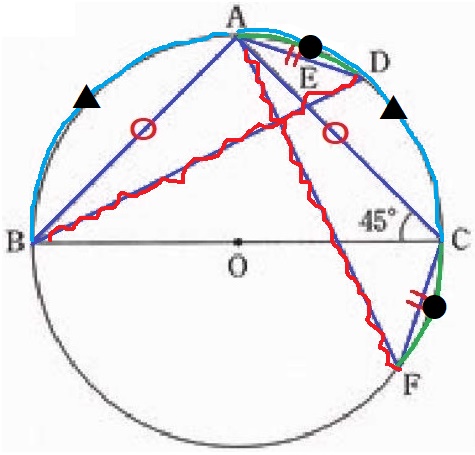
ＢＡ＝ＡＣを弦として眺めると、弧ＢＡ＝弧ＡＣがいえる。
弧ＢＤ＝弧ＢＡ（▲）＋弧ＡＤ（●）＝弧ＡＣ（▲）＋弧ＣＦ（●）＝弧ＡＦ
弦も等しく、ＢＤ＝ＡＦ
３辺が等しいから、△ＡＢＤ≡△ＣＡＦ

（３）
答案では途中の計算も書く。

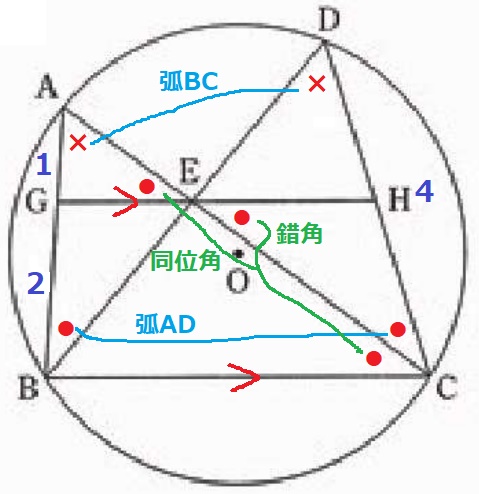
長さの情報が乏しい。。
とりあえず、円周角やＧＥ//ＢＣを使って等角を記しておく。
ＢＣを１辺とする△ＡＢＣと相似にあたるのは△ＡＧＥと△ＤＥＣ。
この２つの三角形を意識しつつ、どこかに長さの比がわかりそうな∽はないか。。

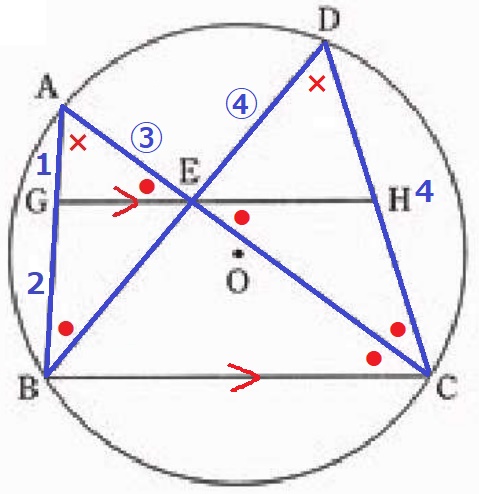
△ＡＢＥ∽△ＤＣＥより、ＡＥ：ＤＥ＝ＡＢ：ＤＣ＝③：④

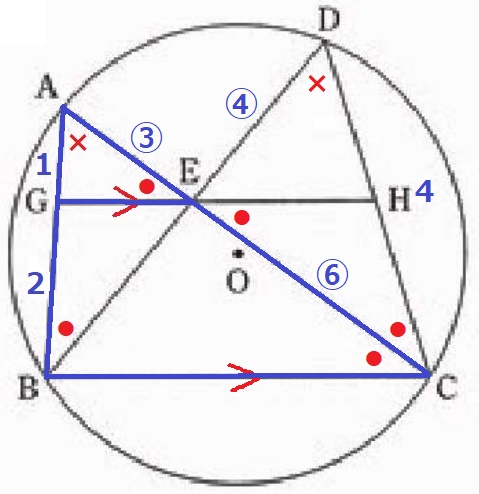
ＧＥ//ＢＣより、ＡＥ：ＥＣ＝ＡＧ：ＧＢ＝１：２
ＥＣ＝③×２＝⑥

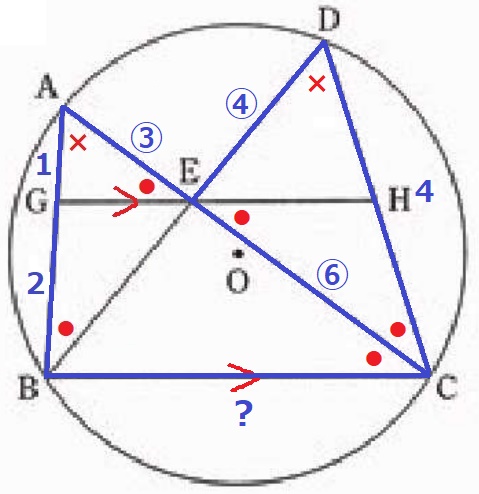
△ＡＢＣ∽△ＤＥＣより、ＡＢ：ＢＣ＝ＤＥ：ＥＣ＝④：⑥
ＢＣ＝３×⑥/④＝９/２ｃｍ