2020年度　宮城県公立高校入試過去問【数学】解説

平均44.5点（前年比；－1.4点）
問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）
７－12
＝－５

（２）
－９/10÷５/４
＝－18/25

（３）
３（４ｘ＋ｙ）＋２（－６ｘ＋１）
＝12ｘ＋３ｙ－12ｘ＋２
＝３ｙ＋２

（４）
６ａ²ｂ×２ｂ÷３ａｂ
＝４ａｂ

（５）
√32－√18＋√２
＝４√２－３√２＋√２
＝２√２

（６）
ｘ²－５ｘ－24
＝（ｘ＋３）（ｘ－８）＝０
ｘ＝－３、８

（７）
試しにａ＝－３を代入してみる。負の数の代入はカッコでくくること！
ア：２ａ＝－６　イ：－（－３）²＝－９　ウ：｛－（－３）｝²＝３²＝９
エ：－√（－３）²＝－√９＝－３　オ：√（－３）²＝√３
ウ・オ

（８）
△ＡＢＤの内角は30°－60°－90°

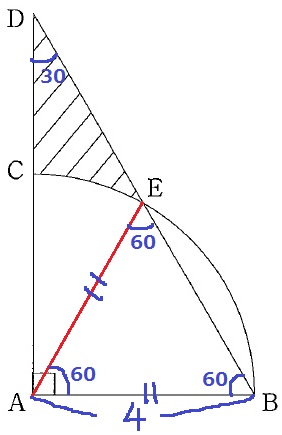
求積すべき範囲の頂点の１つがＥ。
また、Ｅは円周上の点でもあるので、Ｅと中心Ａを結んでみる。
∠ＥＢＡ＝60°、半径からＡＥ＝ＡＢ
△ＡＢＥの内角がすべて60°となり、△ＡＢＥは正三角形。

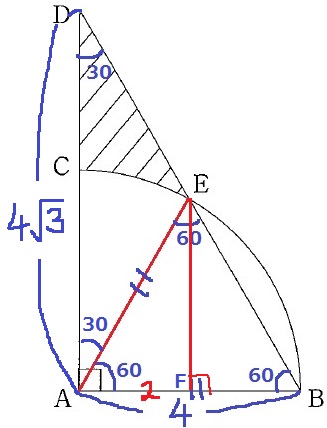
∠ＣＡＥ＝90－60＝30°
△ＡＥＤから扇形ＡＥＣ（半径４ｃｍ中心角30°）をひけば斜線部分の面積がでる。
△ＡＢＤの辺の比１：２：√３から、ＡＤ＝４√３ｃｍ
△ＡＥＤの高さは、Ｅから垂線をおろし、ＡＢとの交点をＦとしたときのＡＦ＝２ｃｍ
４√３×２÷２－４×４×π×30/360
＝４√３－４/３πｃｍ²

大問２（小問集合２）

（１）①文字式
『ＡはＢより４歳年上』
Ａの年齢をｘ歳とすると、Ｂの年齢はｘ－４歳。

②
Ｃの年齢は、（ｘ＋ｘ－４）×２＝４ｘ－８
18年後で等式を作成。
【現在のＡ＋現在のＢ＋36＝現在のＣ＋18】
ｘ＋（ｘ－４）＋36＝（４ｘ－８）＋18
２ｘ＝22
ｘ＝11（現在のＡの年齢）
ＡとＣの年齢差は、
（４ｘ－８）－ｘ＝３ｘ－８＝33－８＝25歳

（２）①確率
３枚から１枚を取り出しては戻す。
これを３回行うので、３×３×３＝27通り

②
２つ以上連続しない方が少ないので、こちらを考えてあとで全体からひく。
連続しない→ＡとＢが互い違い
〔ＡＢ〕のカードの位置を先に考えるのがコツ。
◆〔ＡＢ〕が０枚
ＡＢＡ・ＢＡＢの２通り。
◆〔ＡＢ〕が１枚
〔ＡＢ〕ＡＢ・Ｂ〔ＡＢ〕Ａ・ＡＢ〔ＡＢ〕の３通り。
◆〔ＡＢ〕が２枚
Ｂ〔ＡＢ〕〔ＡＢ〕・〔ＡＢ〕〔ＡＢ〕Ａの２通り。
◆〔ＡＢ〕が３枚
〔ＡＢ〕〔ＡＢ〕〔ＡＢ〕の１通り。
合計８通り。
同じアルファベットが連続する場合の数は、27－８＝19通り
よって、19/27

（３）①関数
ｙ＝－３/４ｘ²にｘ＝２を代入
→Ａ（２、－３）
Ａを通る、傾きが－１である直線の式を求める。
－３＝－１×２＋ｂ
ｂ＝－１
ｙ＝－ｘ－１

②
ｙ＝－ｘ－１は傾きが負なので、ｘの値が小さければｙの値は大きい。
つまり、ｙ＝２のとき、ｘ＝ａとなる。
２＝－ａ－１
ａ＝－３

ｙ＝－３/４ｘ²において、－３≦ｘ≦２のときのｙ変域を求める。
ｘ＝－３のとき、最小値ｙ＝－27/４
ｘ＝０のとき、最大値ｙ＝０
－27/４≦ｙ≦０

（４）①空間図形
５×５×π×６÷３＝50πｃｍ³

②
Ｑの物理量がわかってないので、比で対処する。

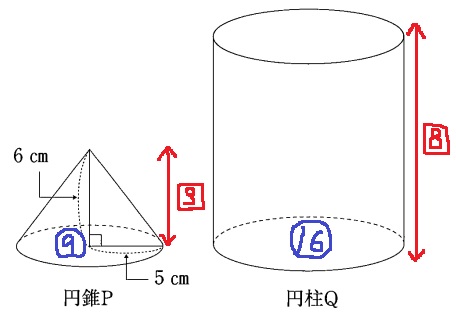
錘であるＰは÷３をすること。
Ｐ：Ｑ＝９×３÷３：16×８＝９：128

大問３（文章題）

（１）①
４分30秒＝4.5分
相対度数は小数で求める。
４÷20＝0.2

②
説明問題。
5.5分未満の相対度数を比較する。
Ａ組…７÷20＝0.35
Ｂ組…８÷25＝0.32
『Ａ組の方が５分30秒未満の割合が大きい』ことから、
Ａ組に速い人が多いと判断した。

（２）①
中学入試っぽい。

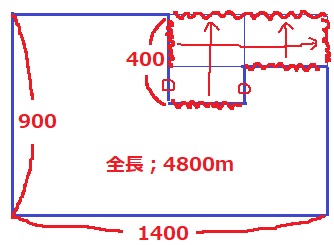
うえのように辺を移動させて長方形にする。
長方形の周の長さは、（900＋1400）×２＝4600ｍ
コースの全長4800ｍで、差の200ｍは〇２つ分となる。
〇＝200÷２＝100ｍ

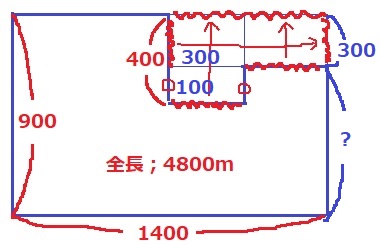
？＝900－300＝600ｍ

②ア
前問の正答が条件。
学校からチェックポイントまでは、1400＋600＝2000ｍ
【1500ｍで６分】なので、チェックポイントまでは、
６分×2000ｍ/1500ｍ＝８分

横軸が時間ではなく、距離になっている点に気をつけること！
原点から（２ｋｍ、８分）まで線をひく。

イ
チェックポイント通過後、残りの距離は4800ｍ－2000ｍ＝2.8ｋｍ
到着予定時間まで、24－８＝16分

はじめは１ｋｍ６分の速度、つぎに１ｋｍ3.5分の速度で走る。
速さは〔分速/ｋｍ〕で換算するのがポイント。
分速１/６ｋｍ→分速１/3.5ｋｍ
求めたいものは分速１/3.5ｋｍで走った距離なので、これをｘｋｍとする。
分速１/６ｋｍで走った距離は2.8－ｘｋｍ。
時間で等式を作成。
ｘｋｍ÷分速１/3.5ｋｍ＋（2.8－ｘ）ｋｍ÷分速１/６ｋｍ＝16分
3.5ｘ＋６（2.8－ｘ）＝16
2.5ｘ＝0.8
ｘ＝８/25
８/25ｋｍをｍに変換。
８/25×1000＝320ｍ
*本問のやりにくいポイントは、速さが『1000ｍあたりの時間（分）』で与えられていること。
一定の距離が１ｋｍなので、速さは分/ｋｍを選択した方がいいかも。

大問４（平面図形）

（１）
直径ＡＢに対する円周角∠ＡＤＢ＝90°
△ＡＤＢで三平方。ＢＤ＝√７ｃｍ

（２）①
台形の証明→１組の対辺が平行である。

円外では角度が使いにくいので、辺の長さに注目する。
ＡＤ：ＤＣ＝３：1.5＝２：１
ＡＢ：ＢＥ＝４：２＝２：１
ＡＤ：ＤＣ＝ＡＢ：ＢＥより、三角形と線分の比の逆からＤＢ//ＣＥ
したがって、１組の対辺が平行であることから四角形ＢＥＣＤは台形となる。
*三角形と線分の比は、２本の平行線より２つの三角形（本問では△ＡＤＢと△ＡＣＥ）が∽であることから、
ＡＤ：ＤＣ＝ＡＢ：ＢＥを導く手法で使われやすいが、その逆も真となる。
すなわち、２組の辺の比が同じであれば、２本の線分は平行といえる。

＠別解＠
△ＡＤＢと△ＡＣＥが２辺の比とあいだの角が等しい→∽
ここから、∠ＤＢＡ＝∠ＣＥＡの同位角が等しい点を指摘して平行を証明してもいい。

②

△ＡＤＢの面積…３×√７÷２＝３√７/２ｃｍ²
ＡＢ：ＡＥ＝４：６＝２：３より、
△ＡＤＢの面積を②とすると、△ＡＤＥの面積は③となる。
３√７/２×３/２＝９√７/４ｃｍ²

＠別解＠
ＤＢ//ＣＥより、等積変形で△ＤＣＢ＝△ＤＥＢ
これらに△ＡＤＢを足すと、△ＡＣＢ＝△ＡＤＥがいえる。
△ＡＤＥの面積は、4.5×√７÷２＝９√７/４ｃｍ²

③
ムズイ:;(∩´＿`∩);:
どこかで複雑な計算処理をしなければならないが、どこでそれをするか。

ＤＢ：ＣＥ＝２：３より、ＣＥ＝３√７/２ｃｍ
Ｆは円周上の点ではないので、邪魔な円を消して見ました。
ＡＦを延長して交点をＧとおく。
チェバの定理からＣＧ：ＧＥを求める。
ＣＤ/ＤＡ×ＡＢ/ＢＥ×ＥＧ/ＧＣ＝１
１/２×２/１×ＥＧ/ＧＣ＝１
ＣＧ：ＧＥ＝１：１（ＧはＣＥの中点にあたる）

ＣＧ＝３√７/２÷２＝３√７/４
同位角より、∠ＡＣＧ＝90°
面倒くさいが・・△ＡＣＧで三平方をする。
ＡＧ＝√（4.5²＋３√７/４²）
＝√（81/４＋63/16）
＝√387/16＝３√43/４ｃｍ

ＡＧとＤＢの交点をＨとする。
△ＢＤＦ∽△ＣＥＦより、ＢＦ：ＦＣ＝ＢＤ：ＣＥ＝２：３
さらに、△ＢＦＨ∽△ＣＦＧより、ＨＦ：ＦＧ＝②：③
△ＡＤＨ∽△ＡＣＧより、ＡＨ：ＨＧ＝２：１で、
ＨＧ＝⑤ということは、ＡＨ＝⑤×２＝⑩
よって、ＡＦ＝３√43/４×⑫/⑮＝３√43/５ｃｍ