大問１（小問集合）
（１）①
－３＋６
＝３
②
（－２）3÷（－４）
＝－８÷（－４）
＝２
③
（ｘ－ｙ）/３＋（ｘ＋２ｙ）/２
＝｛２（ｘ－ｙ）＋３（ｘ＋２ｙ）｝/６
＝（２ｘ－２ｙ＋３ｘ＋６ｙ）/６
＝（５ｘ＋４ｙ）/６
④
ｘ3ｙ2×（－４ｙ）÷３/２ｘ2ｙ
＝－８/３ｘｙ2
⑤
√54－４√３/√２
＝３√６－２√６
＝√６
（２）
ｘ2＋ｘ－６
＝（ｘ＋３）（ｘ－２）＝０
ｘ＝－３、２
（３）
ｙ＝１/３ｘ2は下に凸のグラフ。
ｘ＝０のとき、最小値ｙ＝０
ｘ＝３のとき、最大値ｙ＝３
０≦ｙ≦３
（４）
補助線を１本ひく。
２つの三角形で、対頂角を除いた２角の和は等しい。
●＋■＝ｘ＋31°
青線の三角形に着目。
ｘ＝180－（45＋32＋31＋36）＝36°
＠別解＠
２つの外角定理で角を集めると、星の先端の和は180°
（５）
数学好きは40人中28人の割合。
350×28/40＝245人
（６）
∠ＡＣＢ＝∠ＡＰＢ→弧ＡＢに対する円周角が等しい。
４点Ａ・Ｂ・Ｃ・Ｐは同一円周上にある。
円の中心が知りたい。△ＡＢＣの各頂点を通る円を作図する。
①ＡＢの垂直二等分線
②ＡＣの垂直二等分線（ＢＣでも良い）
③これらの交点●が円の中心。グルっと円を描き、ＯＡとの交点がＰになる。
大問２（関数）
（１）
ｙ＝ａｘ2にＡ（２、２）を代入。
２＝４ａ
ａ＝１/２
（２）
ｙ＝１/２ｘ2にｙ＝８を代入→ｘ＞０より、Ｂ（４、８）
ＣＢに補助線。
△ＯＡＢ＝△ＯＡＣ→等積変形より、ＯＡ//ＣＢ
ＣＢの傾きはＯＡと同じ１。
Ｂから左に４、下に４移動してＣ（０、４）
Ｃ（０、４）→Ａ（２、２）
右に２、下に２だから、傾きは－２/２＝－１
ｙ＝－ｘ＋４
（３）
Ｅのｘ座標をｔとして、各座標をｔで表す。
Ｅ（ｔ、－ｔ＋４）Ｇ（ｔ、１/２ｔ2）
ＯＢ；ｙ＝２ｘ→Ｆ（ｔ、２ｔ）
ＥＦ＝（－ｔ＋４）－２ｔ＝－３ｔ＋４
ＦＧ＝２ｔ－１/２ｔ2
（－３ｔ＋４）：（２ｔ－１/２ｔ2）＝５：４
内項と外項の積で、10ｔ－５/２ｔ2＝－12ｔ＋16
５/２ｔ2－22ｔ＋16＝０ ←２倍
５ｔ2－44ｔ＋32
＝（５ｔ－４）（ｔ－８）＝０
ＥはＤ座標より右（Ａ座標より右）だから、０＜ｔ＜２より、ｔ＝４/５
ｙ＝－ｔ＋４にｔ＝４/５を代入→ｙ＝16/５
Ｅ（４/５、16/５）
大問３（確率・方程式）
（１）①
全体は６×６＝36通り
１回裏返すと黒。
１回目に左端、２回目に右端は必ず裏返す。
すべて黒にするには１回目と２回目の和が６、
すなわち、１回目の矢印と２回目の矢印がぶつかる『あいだの５ヵ所』だから５通り。
確率は５/36
②
６枚のうち黒が少ないので、黒は０～２枚のいずれか。
黒で場合分けする。
●黒が０枚
すべて白は全裏返し２回。（６、６）
●黒が１枚
折り返し１回で黒。
両端から折り返すので、黒は端から連続する並びになる。
黒１枚は両端のいずれかが黒。（６、５）（５、６）
●黒が２枚
左右２個→（６、４）（４、６）
両端１個ずつに注意！（１、１）だけでなく（５、５）も含まれる。
計７通り、確率は７/36
（２）①
からあげ…400×15/10＝600円
とり天…300×16/10＝480円
②
からあげをｘパック、とり天をｙパックとする。
パックの合計数で等式。
ｘ＋ｙ＝200 …①
『すべて定価で売れた場合の利益の合計より10560円少なかった』
値引きの合計が10560円になる。
からあげは0.2ｘパック、とり天は0.3ｙパック値引きされたから、
0.2ｘ×200＋0.3ｙ×240
＝40ｘ＋72ｙ＝10560 ←÷８
５ｘ＋９ｙ＝1320 …②
②－①×５をすると、４ｙ＝320
ｙ＝80
①に代入、ｘ＝200－80＝120
からあげ…120パック
大問４（データの活用）
（１）
27.0～27.5℃の階級の階級値である27.25℃
（２）①
Ａ：25年の中央値（Q2）は上から13番目。
期間１のQ2は25.5℃未満だから、25.5℃超は13年もない。
イ
Ｂ：範囲＝最大値－最小値
期間２より期間３の方が大きい。
ア
Ｃ：期間４のQ2から13番目は27.1℃程。
27.0～27.5℃の詳細はこれ以上わからない。
27.0℃未満と27.5℃超のどちらが多いかは不明。
ウ
②解答例：第３四分位数と第１四分位数の差である四分位範囲は箱ひげ図の箱であり、
期間４の箱が一番右にあるため、期間４の７月の平均気温は以前より高くなっている傾向にあるといえる。
*四分位範囲＝第３四分位数（Q3）－第１四分位数（Q1）
四分位範囲は中央に集まる約50％のデータの散らばり具合を示す。
箱ひげ図でいう箱が四分位範囲で、箱が右にあるほど平均気温が高いことを示す。
箱の説明に第３四分位数と第１四分位数をチョイスする。
大問５（空間図形）
（１）①
辺ＧＨは辺ＥＤと一致する。
点Ｈと重なるのは点Ｂ、Ｄ
②
四角錐の高さはＡＣ＝10ｃｍ
４×４×10÷３＝160/３ｃｍ3
（２）
先に四角錐をＰ、Ｑ、Ｒを通る平面で切断する。
この切断面は底面ＣＤＥＦに平行で、Ｒの左をＵとするとＵはＡＤの中点である。
四角錐Ａ―ＰＵＲＱ：四角錐Ａ―ＣＤＥＦの相似比は１：２
体積比は相似比の３乗→①：⑧
角錐台ＰＵＲＱ―ＣＤＥＦの体積は⑦
さらにＲ、Ｓ、Ｔを通る平面で切断する。
三角錐Ｒ―ＳＥＴと三角錐Ａ―ＵＲＱは底面と高さが等しいから等積。
三角錐Ａ―ＵＲＱの体積は四角錐Ａ―ＰＵＲＱの半分だから（高さ共通、底面半分）、
三角錐Ａ―ＵＲＱ＝三角錐Ｒ―ＳＥＴ＝①÷２＝〇0.5
求積すべき立体の体積は、⑦－〇0.5＝〇6.5
160/３×〇6.5/⑧＝130/３ｃｍ3
大問６（平面図形）
（１）
△ＡＰＣ≡△ＡＱＤの証明。
正三角形の１辺より、ＡＰ＝ＡＱ、ＡＣ＝ＡＤ
正三角形の内角より、∠ＰＡＣ＝60－∠ＣＡＱ＝∠ＱＡＤ
２辺とあいだの角が等しいので合同。
（２）①
前問の合同を使う。
ＱＤに補助線。
Ａを中心に正三角形ＡＰＱを回転させても合同は維持される。
（ＡＰ＝ＡＱ、ＡＣ＝ＡＤ、∠ＰＡＣ＝∠ＱＡＤの２辺とあいだの角は等しい）
合同の対応する辺より、ＰＣ＝ＱＤ
正三角形ＡＰＱより、ＡＰ＝ＰＱ
ＡＰ＋ＢＰ＋ＣＰ＝ＢＰ＋ＰＱ＋ＱＤ
ＡＰ＋ＢＰ＋ＣＰが最も小さくなる。
→ＢＰ＋ＰＱ＋ＱＤが最小→一直線、すなわち、ＢＤの長さに相当する。
正三角形ＡＣＤより、ＤＣ＝５ｃｍ、∠ＡＣＤ＝60°
△ＢＣＤで三平方→ＢＤ＝√41ｃｍ
②
∠ＡＱＤ＝180－60＝120°
合同の対応する角で、∠ＡＰＣ＝120°
∠ＱＰＣ＝120－60＝60°
∠ＢＰＣ＝180－60＝120°
＠フェルマー点＠
△ＡＢＣの各頂点からの距離の和が最短になるＰをフェルマー点といいます。
内角が120°未満の三角形では内部にあり、あいだの角度はいずれも120°になります。
フェルマー点にはいくつかの性質があります。
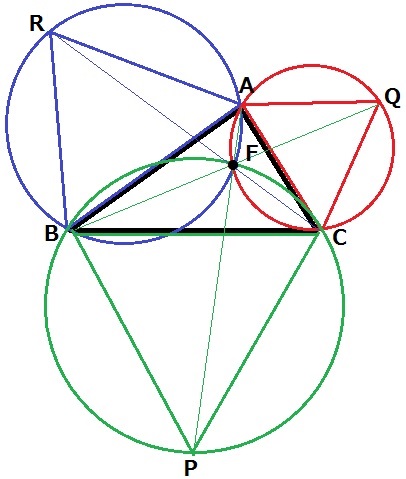
△ＡＢＣの各辺を１辺とする正三角形を追記。
この３つの正三角形の外接円はフェルマー点で交わります。
さらに、うえのようにＡＰ、ＢＱ、ＣＲを結ぶとフェルマー点で交わります。
中学生レベルの数学で証明できますので、一考してみてください。
●講評●
高得点を出せたら自信をもっていい。
大問１
配点率は全体の３割。
（４）星型の問題はどこかで経験しておこう。
（６）正答率は低い。等角から弧ＡＢの円周角→円を見なければならない。
円の中心は∠ＡＣＢ＝90°とは限らないため、垂直二等分線は２本必要になる。
大問２
（２）等積変形→平行を使いこなす。
（３）Ｇが放物線上の点になので、３点のｙ座標をｔで表し、
ＥＦ、ＦＧの長さと５：４の比例式を作るしかない。
大問３
（１）大問の半分だが重い感じがする。①はとりたい。
②個数の少ない黒の方が考えやすい。
１回裏返す黒は端から始まる。あとは（５、５）の組み合わせを出せるか。
2025年広島大問６では同じルールで白１枚になる確率が出題されている。
（２）②少なくなった利益の合計は値引きの合計。
からあげ・とり天１パックあたりの値引き額とパック数を整理する。
大問４
（２）①Ｃ：中央値が27.0℃と27.5℃のあいだにあるため、27.0℃未満と27.5℃超の多寡は不明。
③他県の類題では『箱が右にあるため』と公式解答で複数回みたので、これで良いかと。
箱は四分位範囲。この説明に第１四分位数と第３四分位数をチョイスする。
大問５
（１）②底面の正方形に対して垂直な辺はＡＣ。これが四角錐の高さになる。
（２）２回切断は私立っぽい。わかりやすい面から考える。
面ＲＳＴが厄介か。１階と２階の高さが同じなので、底面が等しい立体を探す。
大問６
2024年鹿児島大問５、2022年滋賀大問４でフェルマー点が出題済み。
今度も公立入試の世界が登場するか!?(;`ω´)
（２）①困ったら前問利用。
合同は維持される。等辺を移す。
置き換えたＢＰ、ＰＱ、ＱＤが最小の長さになるのはどういうことか。
②有名角と睨んで勘で当てた人はいたかも。
30°は使わない。正三角形と対応する角で求まる。
フェルマー点はあいだの角が120°になる。
コメント