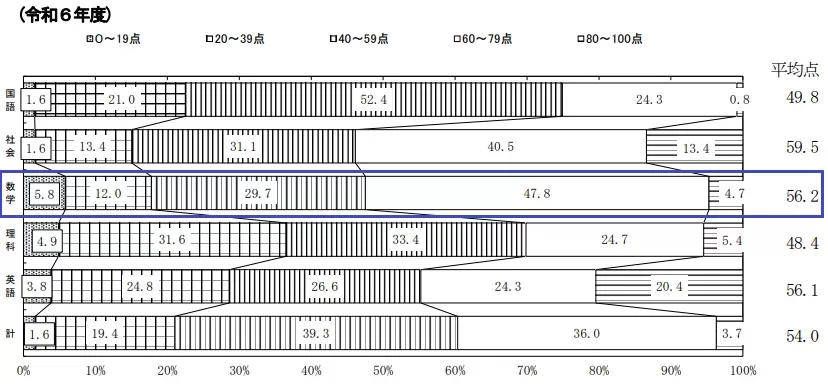
平均56.2点(前年比;-1.1点)
問題はこちら→東進ハイスクールさん(解答)
大問1(小問集合)
(1) 99.4%
6÷(-2)
=-3
(2) 94.9%
3(2x+y)-(x-4y)
=6x+3y-x+4y
=5x+7y
(3) 95.3%
3√5+√20
=3√5+2√5
=5√5
(4) 85.7%
x2+5x+3=0
解の公式を適用して、x=(-5±√13)/2
(5) 83.6%
反比例の比例定数aは積xyで一定。
y=-6×3÷2=-9
(6) 63.8%
絶対値…数直線上で原点0からの距離。
絶対値2以下の整数は、-2、-1、0、1、2。
和は0を中心にプラスマイナスで相殺して0。
(7) 75.9%
4×4×π×6÷3=32πcm3
(8) 92.8%
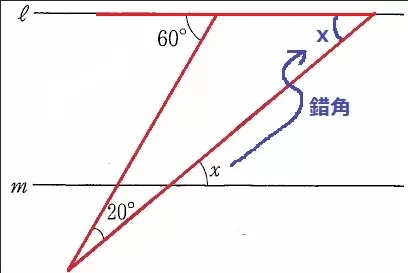
xを錯角であげる。
赤線の三角形で外角定理→x=60-20=40°
大問2(数量変化)
(1) 83.5%
60<x≦180のときなので240円。
(2) 68.0%
P(20、100)→Q(40、120)
右に20、上に20だから、傾きは20/20=1
Pから左に20、下に20移動して、切片は100-20=80
y=x+80
(3) 56.0%
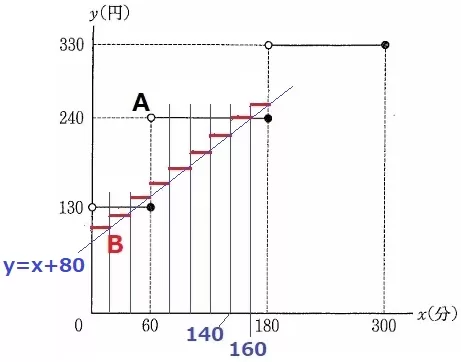
Bをグラフに示すと上図になるが、20円刻みで書くのが大変。
Bは最初が100円で20分ごとに20円あがる。
十の位は必ず偶数なので、y=130円ではなくy=240円でAと交わる。
ここで前問の式を用いる。
y=x+80は階段の右端(●)を通過する直線。
y=240を代入すると、x=160
右端の●が160分だから、140分を超えて160分まで。
イ
(4) 20.9%!
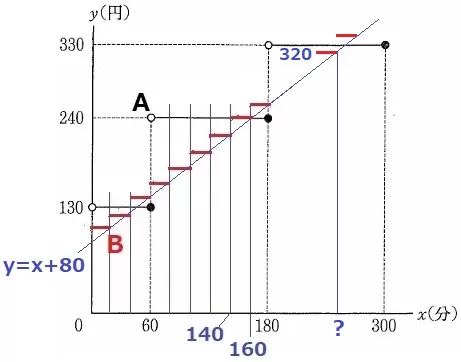
180<x≦300で、Bの方が安い最大のxを求める。
Bの十の位は偶数だから、320円の右端が答えになる。
y=x+80にy=320を代入して、x=240
240分
大問3(整数)
(1)ⅰ…85.6%、ⅱ…74.5%、ⅲⅳⅴ…40.6%
2つの奇数の積は偶奇のどちらか。
2つの奇数を2m+1、2n+1とする。
(2m+1)(2n+1)
=4mn+2m+2n+1
=2(2mn+m+n)+1
2mn+m+nは整数だから、2(2mn+m+n)は偶数である。
2(2mn+m+n)+1は、偶数に1を加えるので奇数。
したがって、2つの奇数の積は奇数である。
同様に考えると、偶数×偶数、偶数×奇数はどちらも偶数である。
ⅰ…2、ⅱ…2mn+m+n、ⅲⅳⅴ…ウ
(2)① 72.5%
全体は6×6=36通り
abが奇数→a・bがともに奇数。
奇数は1・3・5の3つずつだから、3×3=9通り
確率は9/36=1/4
② 42.2%
ab+3b
=b(a+3)=偶数
2数の積は余事象から攻める。
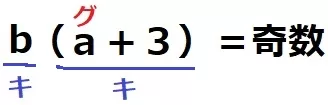
b(a+3)=奇となるには、b=奇、a+3=奇。
→a=偶
b=奇は3通り、a=偶は3通りだから、3×3=9通り
積が偶数となる確率は、1-9/36=3/4
③ 3.2%!!
難しい。

因数分解をすると、(a-2b)(a-3b)
これが3以上の奇数になる。
奇数×奇数=奇数だから、(a-2b)と(a-3b)は奇数である。
a-3bにb=1を代入すると、aは4以上でないと正の数にならないので、
あまりなさそうに思えるが、負の奇数×負の奇数=正の奇数で成立する点に留意したい。
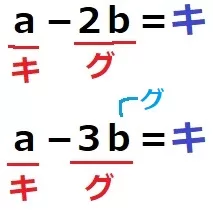
偶奇判定。
a-2b=奇において、2b=偶だからa=奇
a-3b=奇において、a=奇だから3b=偶→b=偶
a=奇、b=偶だから3×3=9通り!…といきたいところだが、
(a、b)=(5、2)を代入すると、(5-2×2)×(5-3×2)=-1で条件不適(´゚д゚`)
両者が負でないと正の数にならない。片方が正だと狂ってしまう。
a-2b<0
a<2b ←これに(5、2)が合わないので×!
計8通りなので、確率は8/36=2/9
@余談@
積が1の場合はないのかと疑問に思う人もいたかもしれない。
a-2b、a-3bには割り算がなく、分数がでてこない。
整数のみの組合せは1×1=-1×(-1)=1。a-2b≠a-3bゆえ積が1はない。
大問4(関数)
(1) 85.1%
y=ax2に(-2、1)を代入。
1=4a
a=1/4
(2) 66.2%
y=1/4x2について、
x=0のとき、最小値y=0
x=4のとき、最大値y=4
0≦y≦4
ア…0、イ…4
(3) 71.2%
y=1/4x2にx=4を代入→B(4、4)
A(-2、1)→B(4、4)
右に6、上に3だから、傾きは3/6=1/2
切片はAから右に2、上に1移動して、1+1=2
y=1/2x+2
(4)① 42.2%
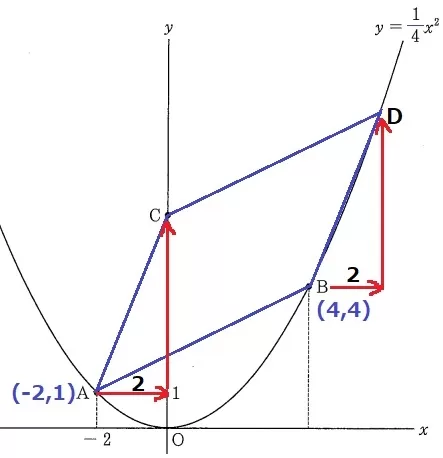
AとCのx座標の差が2→BとDのx座標の差も2。
Dのx座標は4+2=6
これをy=1/4x2に代入、y=1/4×62=9
D(6、9)
② 1.9%!!
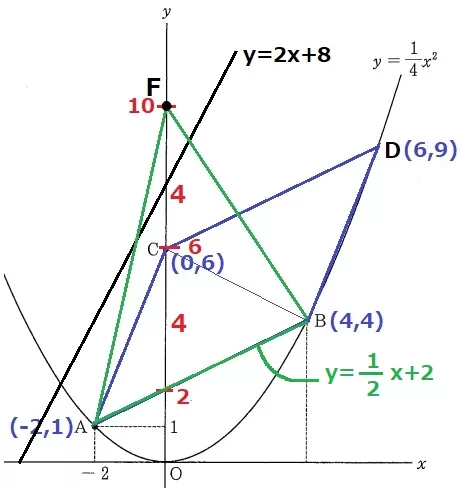
△ABE=平行四辺形ABDC
ABが共通なので、まず、ABを1辺とし、平行四辺形と面積が等しい三角形をつくる。
対角線CBで平行四辺形を分割すると、△ABCと△DBCは等積。
→△ABCを2倍した三角形は平行四辺形と等積。
ABを底辺として高さの比を2倍する。
ポイントは高さの比をy軸上で扱うこと。
ABの切片は2、△ABCの高さの比は6-2=4
Cから上に4移動した点をF(0、10)とすると、△ABF=△ABC×2=平行四辺形ABDC
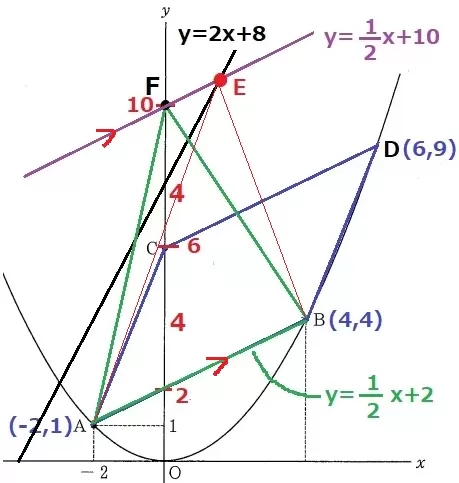
等積変形を用いて、Fをy=2x+8上に乗せる。
Fを通るABに平行な直線の式は、y=1/2x+10
Eはこれとy=2x+8の交点だから、
1/2x+10=2x+8
3/2x=2
x=4/3
y=2x+8に代入→32/3
E(4/3、32/3)
大問5(平面図形)
(1)ⅰ…79.9%、ⅱ…73.0%、ⅲ…72.9%、ⅳ…53.9%
BEを求める下準備として、△ABE∽△EBDを証明する。
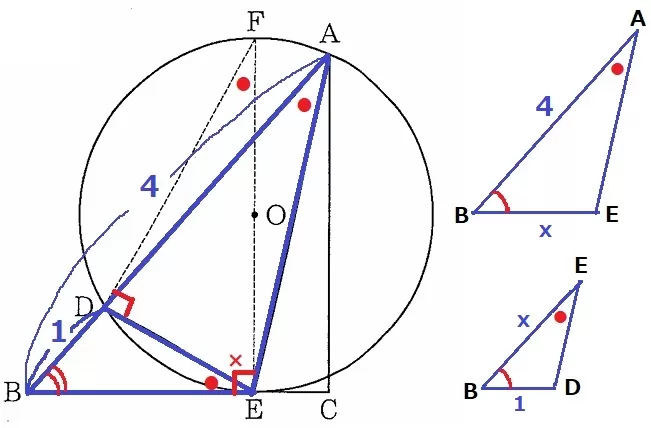
共通角で、∠ABE=∠EBD
弧DEに対する円周角から、∠DAE=∠DFE(●)
半円の弧に対する円周角で∠FDE=90°
△DEFの内角で、∠DFE(●)+∠DEF(×)=90°
半径OE⊥接線BCより、∠DEF(×)+∠BED=90°
よって、∠BAE=∠BED(●)
2角相等から、△ABE∽△EBD
AB:EB=BE:BD
BE=xとおくと、4:x=x:1
内項と外項の積で、x2=4
x>0だから、x=2
ⅰ…エ、ⅱ…ウ、ⅲ…カ、ⅳ…2
(2) 27.3%!
△ABCで三平方→BC=√7cm
CE=BC-BE=√7-2cm
(3) 0.2%!!!
最初のアプローチが肝要。
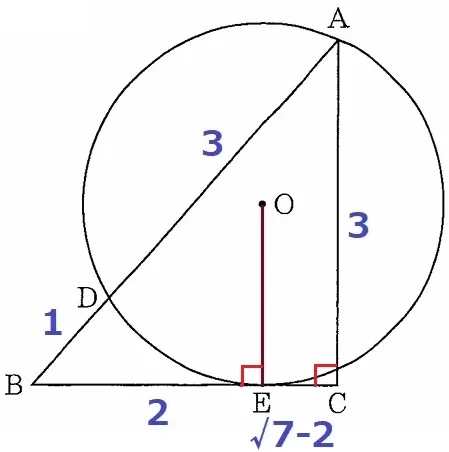
円の半径を求めたいので、中心Oから円周上のいずれかの点と結ぶ。
三平方を用いると想定して直角に目を向けよう。
OE⊥BC→OEを結ぶ。
さらに、ACB=90°、前問のEC=√7-2cmから図形の右側に着目する。
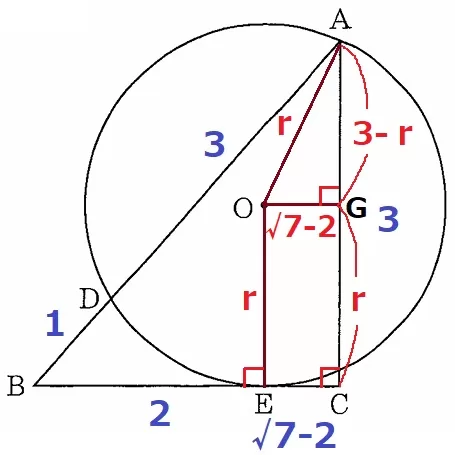
OからACに向けて垂線をひき、足をGとする。
四角形OECGは4角が直角だから長方形。
半径をrとすると、OA=OE=r
長方形の対辺は等しいのでGC=r→AG=3-r
OG=√7-2cm
△AOGで三平方。
r2=(√7-2)2+(3-r)2
r2=7-4√7+4+9-6r+r2
6r=20-4√7
r=(10-2√7)/3cm
大問6(データの活用)
(1) 50.2%
12個の中央値(メジアン)は6番目と7番目の平均。
7と8の平均である7.5日。
(2)① 71.6%
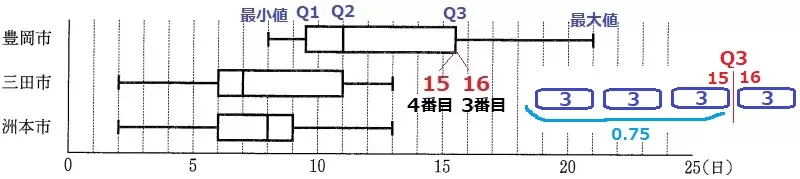
範囲=最大値-最小値
三田市と洲本市は範囲が等しい。〇
平均値を×印などで示す箱ひげ図もあるが、本問はわからない。△
a…ア、b…ウ
② 12.0%!
豊岡市の第3四分位数(Q3)は15.5日。
→3番目が16日、4番目が15日。
累積相対度数…その階級以下の相対度数の合計。
12日以上~16日未満の累積相対度数は、15日以下の相対度数の和である。
豊岡市では12個のうちの4番目以下、つまり下位4分の3までの相対度数の和である。
3/4=0.75
(3)① 6.6%!!

ルール通りに方程式を立てる。
(1~3日のブライアスコア)=(4~6日のブライアスコア)
{(x-0)2+(y-0)2+(0.5-0)2}÷3={(x-1)2+(y-1)2+(0.5-1)2}÷3
x2+y2+0.52=x2-2x+1+y2-2y+1+0.52
2x+2y=2 ←÷2してyについて解く
y=-x+1
② 2.1%!!
これ試験時間内に解ける人いるのか(;´Д`)
工夫しないと計算地獄に陥る。
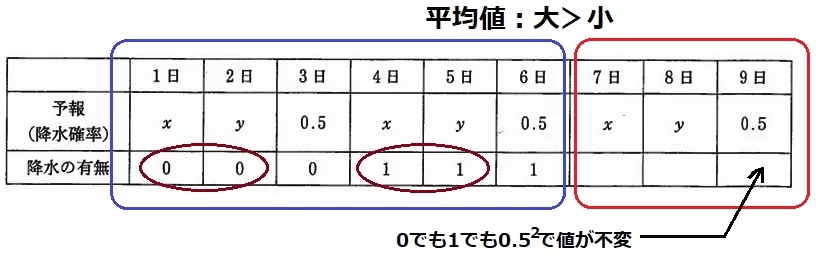
0.5の日は晴れでも雨でも0.52で値は不変である。
平均値は最初の6日間の方が高い。
もし、7・8日目が連続で1だと、1・2日目の〔00〕が足を引っ張り、
全体で均すと1~6日の平均値の方が低くなってしまう。
よって、7か8日のどちらかが晴れ0である。
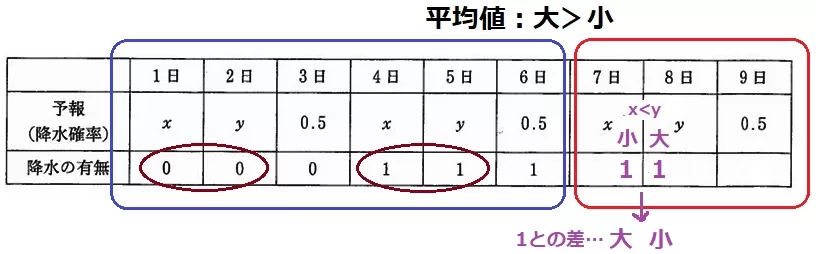
前問より、y=-x+1→x+y=1
『0≦x<0.5、0≦y≦1』の条件と合わせて、x<yがいえる。
x=小、y=大と文字に変えてみると、1との差は大・小と逆転する。
1~6日目は0と1が2つずつ。
もし7日が1、8日が0だと差が大きくなり、ブライアスコアが高くなる。
7日を0、8日を1とすることで、7~9日のスコアを下げる。
したがって、7日が晴れ0、8・9日が雨1である。
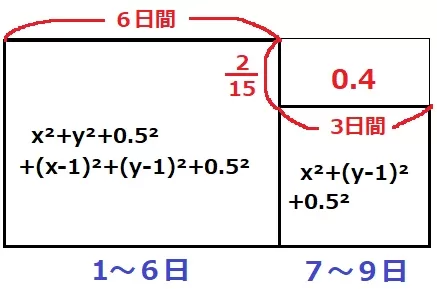
平均を面積図で表す。(横が日数、縦が平均値、面積が総和)
左の上の長方形が、3×2/15=0.4
つまり、7~9日の総和に0.4を足したものを2倍すれば、1~6日の総和に相当する。
計算しんどいです。。
x2+y2+0.52+(x-1)2+(y-1)2+0.52={x2+(y-1)2+0.52+0.4}×2
同じものを消します。
y2+(x-1)2=x2+(y-1)2+0.8
前問のy=-x+1より、y2=(-x+1)2=(-1)2(x-1)2=(x-1)2
(y-1)2=(-x+1-1)2=x2、に変えます。
(x-1)2+(x-1)2=x2+x2+0.8 ←÷2
(x-1)2=x2+0.4
2x=0.6
x=0.3、ウ
●講評●
記述はないが厳しい設問が見受けられる。
大問1
配点24点。
(6)すべての正負が相殺される。
(8)mより下の三角形で外角定理を使ってもいい。
大問2
階段状のグラフ問題では特殊な出し方である。
(2)2点を通る直線の式を求めればいい。
(3)差がつく。Bの十の位に着目してy=240と絞る。
前問で階段の右端●を通過する直線を求めたので、
y=240を代入したときのxの値が最大の時間になる。
(4)300分のAは330円。Bの十の位は偶数だからy=320に絞る。
ここもy=x+80を活用する。
大問3
(1)2( )→偶数、2( )+1→奇数
(2)②因数分解で積の形にまとめる。
式を偶奇判定。2数の積は奇数の方が少ない。
③難問だった。
a、bは1~6の自然数。aから2倍・3倍したbをひいたら負になりやすい。
ここから負×負の組合わせを考えられるか。
さらに仲間はずれが1つある。過去問でも似たような問題が出ているので油断できない。
2022年兵庫(1つだけ底面にない)2021年兵庫(a=0のパターン)
大問4
前半で点を稼ぐ。
(4)②最初はy=2x+8を無視。
共通辺のABを1辺とする平行四辺形と等積の三角形をつくる。
y軸上にできた点を平行移動させてy=2x+8に移す。
大問5
(1)ⅲ対応する辺がごちゃごちゃになったら三角形を描こう。
(3)円周上の点はA・D・E。半径⊥接線からOEは使うはず。
前問のECを三平方で用いるにはどこで直角三角形をつくるか。
大問6
兵庫ラストの曲がり具合( ノД`)
(3)①残り時間との兼ね合いもあるが、ここまでは取れうる。
0.5の場合は雨でも晴れでも値が変わらないことをつかんでおく。
②諦めていい。
晴れ・雨の組み合わせは3通りだが、計算式が長くて大変。
表4の数値の並び、xとyの条件から晴れは7日と定めないと時間が足りない。
平均は面積図で整理することができる。前問の答えからyを消し、xについて解く。
■追記:正答率1%切ると思いきや2%いた。正解した方、おめでとうございます。


コメント
データでまさかの最難関問題が出るとは思いませんでした。でもラス問だし神奈川県が毎年出すアレ(最近は少し改善された)よりはまだマシな出題ですね。
コメントありがとうございます。
曲がった出題でどうしていいのか見当がつきにくく、計算も厄介でした。
兵庫も神奈川も記述力を問わない点で共通していますが、こちらの方が全体のバランスがGOODです。
スポーツクライミングのポイント、ブライアスコアなど、兵庫は新しいことをしたいんですね。2025年はなんでしょう?ボウリングの軌道と相似の利用とか?
コメントありがとうございます。
ブライアスコアはどうやって持ってきたのでしょうね(^^;
ワークや模試にない問題文を出すぞ!という気概を感じます。解答の筋道も特殊ですね。
兵庫は内申点の比率が5割もあるようで、検査点の方で実力差がつきやすい大問を作りたいのかもしれません。
なるほど。例年出される独特の問題は実力差をつけたいという理由からなんですね。時間を削り受験生を焦らせるなかなか怖い問題だと思いました。返信ありがとうございました!