2024年度　鹿児島県公立高校入試問題過去問【数学】解説

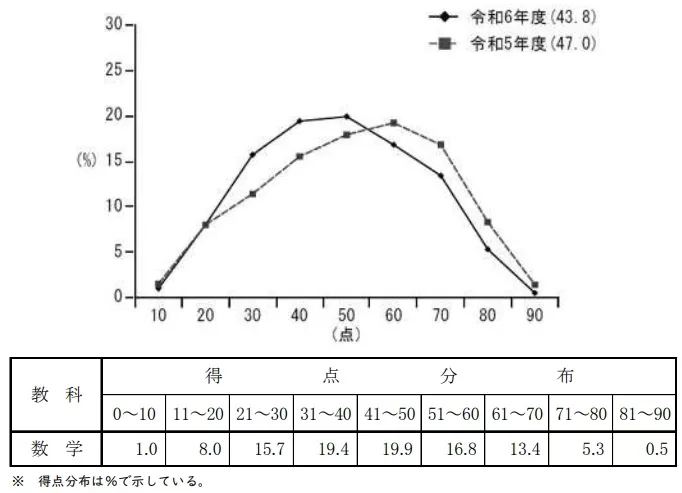
平均43.8点（前年比；－3.2点）

問題はコチラ→ＰＤＦファイル

大問１（小問集合）－63.3％

（１）①　97.8％
41－７×５
＝41－35
＝６

②　91.7％
３/４÷９/８＋１/２
＝２/３＋１/２
＝７/６

③　71.2％
√18－２√３/√６　←後半は√３で約分
＝３√２－２/√２
＝３√２－√２
＝２√２

④　54.7％
72の約数のうち、８の倍数を求める。
72＝８×９
９の約数は１・３・９だから、８×１＝８、８×３＝24、８×９＝72
８、24、72

⑤　84.2％
５で割れる→５でくくれる。
５ｎ、５ｎ＋10＝５（ｎ＋２）
イ・エ

（２）　24.0％！
ａ（ｘ－ｙ）－ｂｘ＋ｂｙ
＝ａ（ｘ－ｙ）－ｂ（ｘ－ｙ）　←共通因数ｘ－ｙ
＝（ｘ－ｙ）（ａ－ｂ）

（３）　38.4％
税抜きを【100】とすると、税込み176円は【110】
176×100/110＝160円

（４）　59.9％

ＦＥ//ＤＣの錯角でｘをおろす。
△ＡＤＣの内角から、180－（60＋69）＝51°

（５）　48.3％
抽出した40個のうち、赤：白＝36：４＝⑨：①
白全部は100個だから、赤全部は100×⑨＝900個

大問２（小問集合２）－51.0％

（１）　60.9％

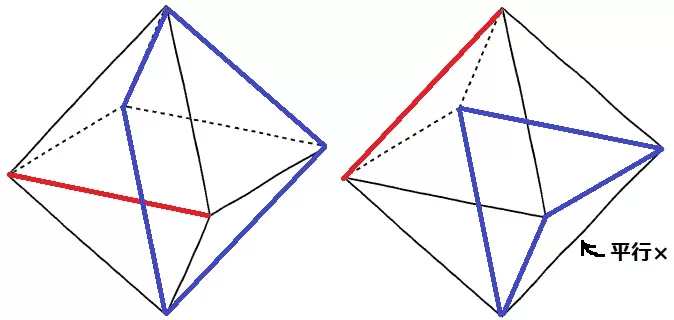
ねじれの位置→延長しても交わらない、かつ平行でもない。
ネジレの本数は横線が４本、斜め線も４本（対辺は平行である）。
内訳は交わるのが６本、平行が１本、残りの４本がネジレである。
正八面体は90°回転で一致するので、どの辺を選んでも４本である。
ア

（２）　48.4％

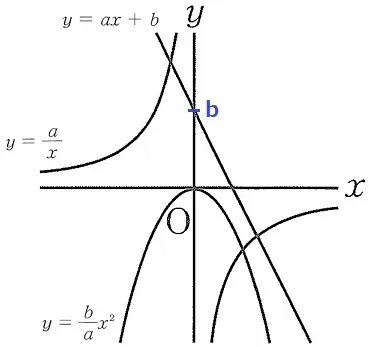
ａ＜０、ｂ＞０
ｙ＝ａｘ＋ｂ…右下の直線、切片ｂは正。
ｙ＝ａ/ｘ…左上（第２象限）と右下（第４象限）の双曲線。
ｙ＝ｂ/ａｘ²…ｂ/ａが負なので、上に凸の放物線。
ウ

（３）　48.2％

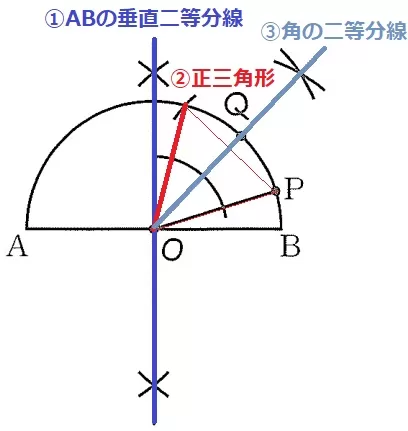
①円の中心Ｏは直径ＡＢの中点→ＡＢの垂直二等分線との交点がＯ。
②【30°＝60°÷２】60°といえば正三角形。
円の半径ＯＰの長さをとり、Ｐに針を合わせて長さを移す。
弧ＡＰとの交点が正三角形の残りの頂点である。Ｏと結ぶ。
③60°の二等分線と弧ＡＰとの交点がＱ。

（４）　68.7％
偶数×偶数＝偶数
Ａはすべて奇数なので、どれを出しても結果に影響はない。
Ｂは２だけ偶数。つまり、Ｂで２が出るか出ないかが重要である。
２が出る確率＝積が偶数となる確率は１/３。

（５）　35.3％
答案では方程式と計算過程も書く。
重さの合計で等式。
ｘ＋ｙ＝240　…①
食物繊維の量で等式。
100ｇあたりなので、÷100をして１ｇあたりになおす。
2200/100ｘ＋2400/100ｙ＝5440
22ｘ＋24ｙ＝5440　…②

②－①×22をすると、２ｙ＝160
ｙ＝80
①に代入、ｘ＝240－80＝160
さつまいも…160ｇ、にんじん…80ｇ

＠がね＠

農林水産省「うちの郷土料理」より。

大問３（データの活用）－64.1％

（１）　47.3％
データを昇順に並べる。
【5.8、9.5、9.8、10.5、12.4、12.6、14.3、16.5、19.9、23.9、24.3、24.9】
12個の中央値は６番目と７番目の平均→（12.6＋14.3）÷２＝13.45≒13.5℃

（２）　83.7％

ア～ウが2002年、エ～カが2022年。
ア・エは度数分布表と階級の幅が同じ。
ウ：正しくは27～33…16日、33～39…15日
オ：正しくは27～31…０日、31～35…24日、35～39…７日
ウ・オ

（３）①　77.8％
手順に従う。
（28＋８）×５÷９＝20℃

②　43.9％
説明問題。
９月
19℃以上21℃未満の階級の相対度数は、グラフより９月の方が大きいから。

（４）①　87.7％

範囲＝最大値－最小値、最も範囲が大きいのは大口。〇
四分位範囲＝第３四分位数（Q3）－第１四分位数（Q1）、箱の長さが最も短いのは与論島。〇
ア

②　71.2％
南にいくほど四分位数は大きくなる傾向にあるが、鹿児島だけ違う。×
イ

③　74.8％
12個の中央値（Q2）は６番目と７番目の平均、Q1は３番目と４番目の平均。

大口のQ1から３つは－４℃未満。
３番目が最小値と考えると、４番目は高くても－１℃程。
しかし、５番目が０℃未満かは不明。Q2が２℃超、Ｑ3が13℃超なので６番目も不明。△
ウ

④　45.0％
Q1が２℃未満であれば、２℃未満が３つ以上が確定。大口しかない。×
イ

大問４（数量変化）－17.8％

（１）　65.7％
ｙ＝１/６ｘ²にｘの値を代入し、該当するｙの値が出ればいい。
ｘ＝18を代入すると、ｙ＝１/６×18²＝54
イ

（２）　22.4％！
ドローンの進む距離ｙは０≦ｘ≦30（30秒経過まで）にｙ＝１/６ｘ²
ｘ＝10→20まで増加したときの変化の割合が求めたい平均の速さにあたる。
ｙ＝ａｘ²において、ｘの値がｐ→ｑに増加するときの変化の割合はａ（ｐ＋ｑ）
１/６×（10＋20）＝秒速５ｍ

（３）①　6.9％!!
答案では方程式と計算過程も書く。

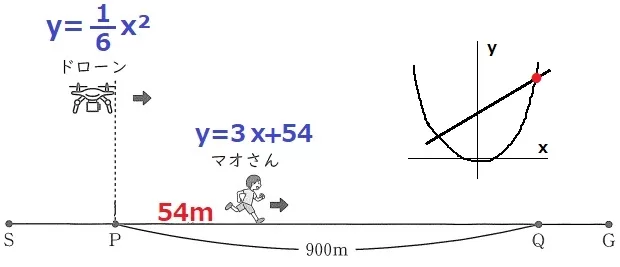
グラフが提供されていないが、グラフの交点のｘ座標を求めればいい。
ｘはドローンがＰ地点を出発してからの時間、ｙはＰ地点からの距離。
マオは秒速３ｍの一定の速さで走る→傾き３
ｘ＝０のとき、Ｐ地点から54ｍ離れているので切片54→マオ；ｙ＝３ｘ＋54

ｔ秒後に追いついたから、ｙ＝１/６ｔ²とｙ＝３ｔ＋54の交点を求める。
１/６ｔ²＝３ｔ＋54　←６倍して整理
ｔ²－18ｔ－324＝０
解の公式を適用して、ｔ＝９±９√５
０≦ｔ≦30より、ｔ＝９＋９√５
９＋９√５秒後

②　2.4％!!

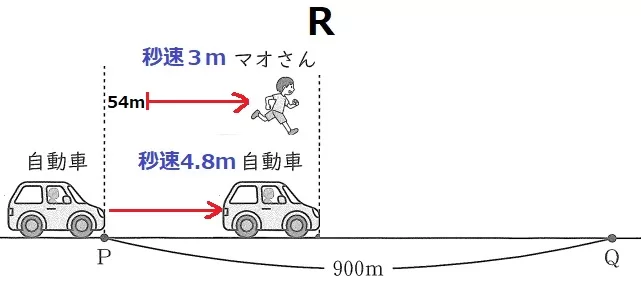
まず、自動車がマオに追いついたＲ地点までの距離を求める。
自動車がＰ地点を出発したとき、両者は54ｍ離れていた。
１秒あたり4.8－３＝1.8ｍ差が縮むので、54÷1.8＝30秒後にマオに追いつく。
ＰＲ間の距離は、4.8×30＝144ｍ
ＲＱ間の距離は、900－144＝756ｍ
したがって、756÷180＝秒速4.2ｍ

大問５（平面図形）－27.1％

（１）　38.8％

正三角形ＢＤＣの内角から∠ＣＢＤ＝60°
これを弧ＣＤの円周角で移して、∠ＣＧＤ＝60°

（２）ａ…82.8％、ｂ…75.9％、ｃ…56.0％、ｄ…52.9％、ｅ…45.6％
前半は△ＢＨＤ≡△ＣＧＤの証明。

△ＢＤＣは正三角形だから、ＢＤ＝ＣＤ
△ＧＨＤも正三角形だから、ＨＤ＝ＧＤ
∠ＢＤＨ＝60°－∠ＢＤＧ、∠ＣＤＧ＝60°－∠ＢＤＧより、
∠ＢＤＨ＝∠ＣＤＧ
２辺とあいだの角が等しいので、△ＢＨＤ≡△ＣＧＤ

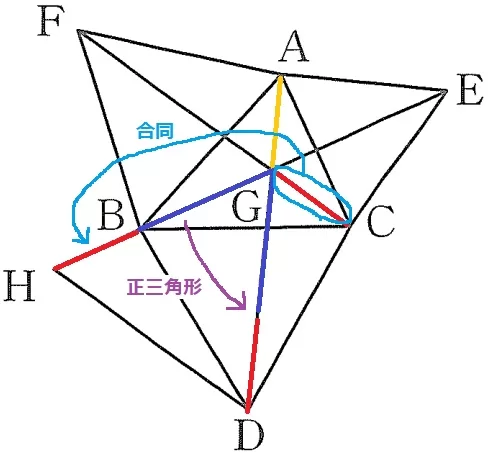
△ＢＨＤ≡△ＣＧＤの対応する辺から、ＣＧ＝ＢＨ
正三角形ＧＨＤより、ＧＨ＝ＧＤ
ＡＧ＋ＢＧ＋ＣＧ
＝ＡＧ＋（ＢＧ＋ＢＨ）
＝ＡＧ＋ＧＨ
＝ＡＧ＋ＧＤ
＝ＡＤ
ａ…エ、ｂ…ア、ｃ…キ、ｄ…コ、ｅ…シ

（３）①　20.5％！
ＧＤ
＝ＡＤ－ＡＧ
＝（ＡＧ＋ＢＧ＋ＣＧ）－ＡＧ
＝ＢＧ＋ＣＧ
＝５＋３＝８ｃｍ

②　0.4％!!!
答案では求め方や計算過程も書く。
相似で求めようとすると失敗する。

（１）の∠ＣＧＤ＝60°に着目する。
ＣからＧＤに垂線、足をＩとする。
△ＣＧＩの内角は30°―60°―90°だから、辺の比が１：２：√３の直角三角形。
ＧＩ＝３/２、ＣＩ＝３√３/２
ＩＤ＝８－３/２=13/２
△ＩＤＣで三平方→ＣＤ²＝（３√３/２）²＋（13/２）²＝49
ＣＤ＞０より、ＣＤ＝７

③　0.1％!!!

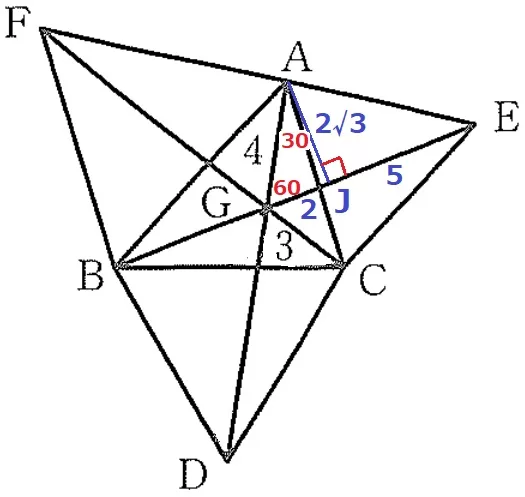
２つとも正三角形なので、△ＡＣＥの１辺の長さがわかれば面積比も出る。
前問と同じように、ＡからＧＥに垂線をひいて足をＪとすると、
△ＡＧＪの辺の比から、ＧＪ＝２、ＡＪ＝２√３
ＧＥ＝ＡＧ＋ＧＣ＝７だから、ＪＥ＝７－２＝５
△ＡＪＥで三平方→ＡＥ＝√37

△ＢＤＣ：△ＡＣＥの相似比は７：√37。
面積比は相似比の２乗→△ＢＤＣ（Ｓ）：△ＡＣＥ（Ｔ）＝49：37

@別解@

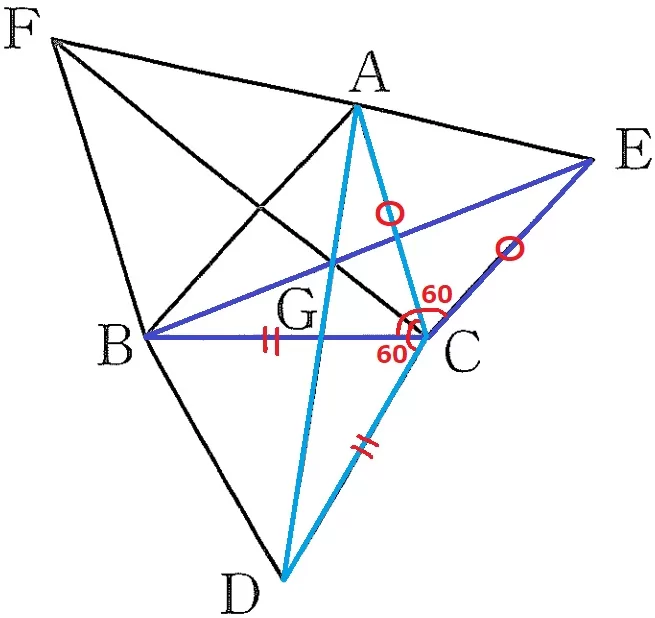
△ＡＤＣと△ＥＢＣは２辺とあいだの角が等しいので合同。
（あいだの角度は60°＋∠ＡＣＢで共通）

ＡＧ：ＧＤ＝△ＡＧＣ：△ＤＧＣ＝④：⑧
ＢＧ：ＧＥ＝△ＢＧＣ：△ＥＧＣ＝⑤：⑦
△ＡＤＣ＝△ＥＢＣ＝⑫だから、同じ面積比として扱える。

ＢＣとＧＤの交点をＫとする。
角の二等分線の定理から、ＢＫ：ＫＣ＝ＧＢ：ＧＣ＝５：３
（２角相等の△ＧＤＣ∽△ＣＤＫからでも説明できる。
ＧＤ：ＧＣ＝ＣＤ：ＣＫ＝８：３→ＢＣ＝ＤＣ＝８→ＢＫ＝８－３＝５）
四角形ＢＤＣＧ＝⑧×８/３＝〇64/３
△ＢＤＣ＝〇64/３－⑤＝〇49/３

同様に、ＡＣとＧＥの交点をＬとする。
ＡＬ：ＬＣ＝４：３
四角形ＣＥＡＧ＝⑦×７/３＝〇49/３
△ＡＣＥ＝〇49/３－④＝〇37/３
したがって、△ＢＤＣ（Ｓ）：△ＡＣＥ（Ｔ）＝〇49/３：〇37/３＝49：37

＠余談＠

面積比を整数比になおすとこうなります。

…よくみると、隣り合う２辺の和の２乗が面積比になっている。
四角形ＡＦＢＧ＝（ＡＧ＋ＢＧ）²＝（４＋５）²＝81
四角形ＢＤＣＧ＝（ＢＧ＋ＣＧ）²＝（５＋３）²＝64
四角形ＣＥＡＧ＝（ＣＧ＋ＡＧ）²＝（３＋４）²＝49
果たして偶然なのか…原理をご存じの方はコメント欄かお問い合わせよりお知らせ願います。

＠＠
ピコピコさんからありがたいコメントを頂きました。

問題のように、60°と垂線の利用で解決しました。四角形ＡＦＢＧの面積を考えます。
（３）①のように考えると、ＦＧ＝ＡＧ＋ＢＧ
四角形ＡＦＢＧの底辺をＦＧとします。
高さの合計は有名三角形から、√３/２ＡＧ＋√３/２ＢＧ＝√３/２（ＡＧ＋ＢＧ）＝√３/２ＦＧ
四角形ＡＦＢＧの面積は、ＦＧ×√３/２ＦＧ÷２＝√３/４ＦＧ²
同様に、四角形ＢＤＣＧは√３/４ＤＧ²、四角形ＣＥＡＧは√３/４ＥＧ^２なので、
面積比は、ＦＧ²：ＤＧ^２：ＥＧ²＝（ＡＧ＋ＢＧ）²：（ＢＧ＋ＣＧ）²：（ＣＧ＋ＡＧ）²となります。

＠＠
谷津綱一さんから素晴らしい解法を頂きました。

谷津綱一さんのnoteより。
『高校への数学』の執筆もされているベテランの先生です。
（２）のように、四角形ＧＣＥＡ側でも△ＧＩＥが正三角形となるような点Ｉをつくり、
△ＣＩＥ≡△ＡＧＥから四角形ＧＣＥＡを△ＧＩＥに変形します。
太線の正三角形からそれぞれ△ＧＢＣと△ＧＣＡをひけば、求めたい正三角形の面積比になります。
最後から２行目は隣辺比で、角の和が180°の場合も隣辺比が使えます。
整数のみの簡単な計算で求まるベスト解だと思います。

＠フェルマー点＠
本問の点Ｇはフェルマー点というそうです。2022年滋賀（大問４）で出題されています。

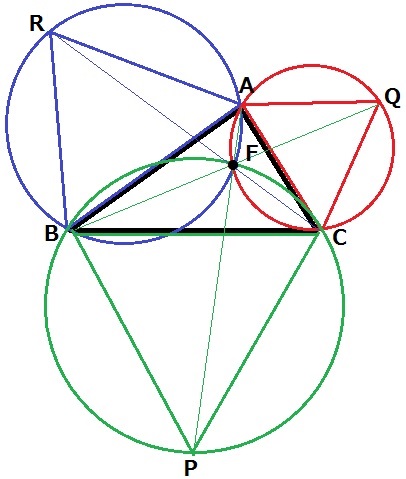
フェルマー点は３つの頂点からの距離の和が最短になります。
内角が120°未満の三角形では内部にあり、あいだの角度はいずれも120°です。
（∠ＡＦＢ＝∠ＢＦＣ＝∠ＣＦＡ＝120°）
三角形の各辺の外側に正三角形をつくり、正三角形の外側の点と反対側の三角形の点を結ぶと、
３本はフェルマー点で交わります。さらに、３つの外接円もフェルマー点で交わります。
公立高校入試解説ページに戻る